The Vogel Spiral Phenomenon

• Download full project source - 8 Kb

Introduction

It looks like there is the infinite variety of spirals [1-11]. But sometimes, spirals are not looking as we expect, especially many Vogel's spirals, also polyspirals and many special type of spirals, e.g., Ulam spiral, spiral matrix, etc.

Remark: H. Vogel in [5, p.182] called his spirals differently: "For lack of a better term, we will call the spiral ... a cyclotron spiral."

Here is a simple definition for the general spiral term from Wikipedia [1]:

Here is another handy definition from RosettaCode Wiki [2]:

The goal of this article is to prove that spiral images could be very tricky and confusing, not looking as a spiral at all. But such look is real, and it would be explained why this phenomenon is happening.

Not clear what is "wholly mathematical construction program" [5]? But in [5-7] a computer was used for sure to calculate and show spiral.

Also, take into account that those days computers were different and slow. As H. Vogel explained in [5]: "All figures have been photographed from a PDP-12 screen." It looks like they were using one ASCII symbol looking as a big dot, because they have no software to plot using lines.

In [7] it was mentioned that T.A. Davis used help of an artist, so, spirals were "constructed" and manually painted in some cases.

About Vogel Spirals

To the phenomenon of some interesting and intriguing pattern devoted many articles [5-8] and much more after [5]. All started many years ago with innocent study of the patterns discovered on sunflower and daisy heads [8], and it never ended.

In [7] was proposed so called "golden angle", also called "Fibonacci angle":

In [5, p. 180] was proposed the following formula ("translated" to our notation now):

A few additional important for us points could be found in [5] (stressed here):

All these words "approximately", "irregularities" and "controversial" are telling us about hesitation. They were seeking the precise solution, but they were seeking it in the sunflower head, not in the spiral. And, by the way, they called it cyclotron spiral. May be, trying to separate it from regular "visible" spiral? It is quite correct: what they have built is not looking as a spiral at all! Anyway, now this kind of spirals is called the Vogel spirals.

The following JavaScript fragment shows how any Vogel spiral is generating and plotting, including setting selected plotting style, i.e., plotting using dots or lines.

// setting ctx styles: colors, plotting units (dots/lines)
// canvas size - cw x cw; canvas center - cc; scale - sc.
ctx.fillStyle="white"; ctx.fillRect(0,0,cw,cw); // cleaning canvas
if(pu=="d") {ctx.fillStyle=clr; } // pu - plotting unit ("d"-dot, "l"-line)
else {ctx.strokeStyle=clr; ctx.beginPath(); ctx.moveTo(cc, cc);} // Lines
// Prime loop: generating/plotting Vogel spiral
for(var i=0; i<n; i++) {
  // Calculating polar coordinates theta (t) and radius (r)
  t=it*i; r=Math.sqrt(i/n);
  // Converting to the Cartesian coordinates x, y
  x = sc*r*Math.cos(t) + cc; y = sc*r*Math.sin(t) + cc;
  if(pu=="d") {bDot(x,y,5)} // Dots
  else {ctx.lineTo(x, y);}  // Lines
}//fend i
if(pu=="l") {ctx.stroke()}  // Lines

As you can see, it's pretty simple, just 10 lines of the code (in the typical plotting spiral prime loop).

In many cases, a loop generating any spiral has the same structure (shown above), which is reflecting the fact that using the polar coordinate system [1,3] is more appropriate for any spiral. So, in polar coordinates most spirals (and other figures) having unique equation/function like following: r = f(theta), where the radius r is a monotonic continuous function of the angle theta.

The polar coordinates r and theta can be converted to the Cartesian coordinates x and y as following [3]: x=r*cos(theta) and y=r*sin(theta).
Note: in the fragment above t is used instead of theta.

There are only 2 essential coefficients, that would be used to change a spiral "look and feel": it - an initial angle theta and n - a number of dots. All others are constants, e.g., canvas dimensions, a scale, etc. But it was interesting to play with them too.

Note: The first spiral in the [Fig.1a] below is the most famous one. It would be called "canonical" Vogel spiral here. All other figures plotted in dots were partially inspired by [6,10].

See them all for yourself in figures below, where each figure Na (in dots) and Nb (in lines) has 3 spirals plotted using the same initial angle it and the same number of dots n.

In addition, to show clearly our point, the 2nd and the 3rd spirals (in the figures Nb) are plotted using both dots and lines (e.g., see [Fig.1b/2-3]).

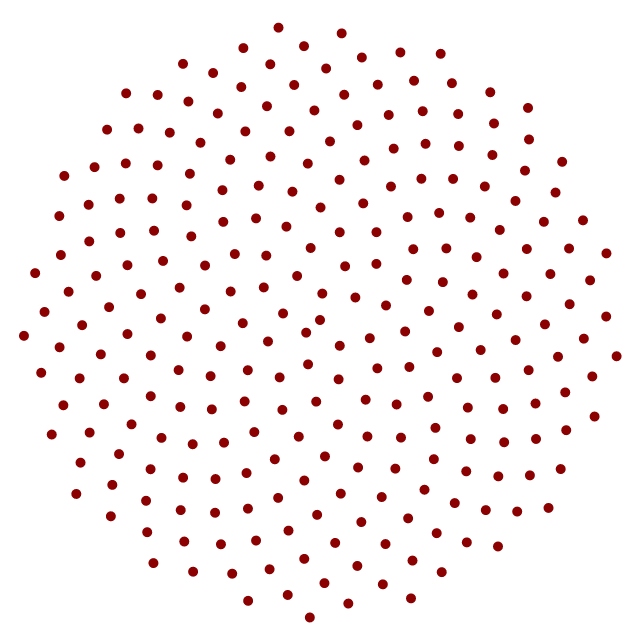
The first spiral in the [Fig.1a] above is the canonical Vogel spiral. Sometimes it is called also a "sunflower seeds/florets".
Brief description notes for [Fig.1a]:

• The canonical Vogel spiral has many visible clockwise and counterclockwise secondary spiral arms. But is it a spiral?
• The second spiral has no any obvious pattern, still not looking as a spiral. I was skeptical that some angle can be "golden". But at this point I was not so sure... Although, if number of dots is low then even "golden" angle cannot help. E.g., [Fig.1a/2,3]
• The third spiral has some secondary spiral arms, still not looking as a spiral.

A picture is different if 2 consecutively generated dots are connected with line segments, i.e., spiral is plotted using lines.

Brief description notes for [Fig.1b]:

• The first spiral now looks like sunflower head. Hard to believe it is a spiral.
• The second spiral is definitely a spiral! Finally! But it's looking more like a polyspiral with overlapping line segments.
• Only looking at the central area of the third spiral it is possible to realize: it is a polyspiral! In turn, it proves that the first spiral is a polyspiral too.

• Anybody looking at the Vogel spiral in big dots (in Na/1 figures) cannot see any spiral. We all are not delusional! Simply our vision depends on our brain, and the latter is offering us clockwise and counter clockwise secondary spiral arms. And they are real. To prove to yourself that this is real - simply print the first image and connect dots in arms with color pens.
• All spirals in Fig.Na are spirals for sure, but spiraling is hidden from the viewer. Nb figures provide us with the proof.

My friend (who is a musician) asked me: "Why do you insist that 2nd spiral (in [Fig.1b]) is a spiral? Explain it for me please! I see lines and dots, but there is no any spiral?!" I tried a few "reasons", but it didn't work. Until I've said: "Because this curve started in the center of the canvas and visibly looping around the central point, plus it is always making loops bigger". He was satisfied.
 

Brief description notes for [Fig.2a]:

• The first spiral at the central area looks as a spiral. But then it shows us a lot of clockwise spiral arms.
• The second and the third images are single spiral arms.

Brief description notes for [Fig.2b]:

• It is very clear that the first spiral is a real spiral starting in the center. In addition, this is a very smooth spiral, although still it is a polyspiral. No visible line segments or secondary spiral arms at all.
• It should be emphasized, that any spiral plotted using lines is a polyspiral. If plotting angle is tiny, then spiral is looking as a smooth one. Sometimes, spiral is looking smooth closer to the center, but closer to the canvas borders line segments are becoming visible.
• The second and the third images are single spiral arms.

Brief description notes for [Fig.3a]:

• All 3 spirals are not looking as spirals. The first one at the central area looks as having 9 spiral arms. But then it shows us a lot of clockwise spiral arms.
• The second and the third images are looking having many single spiral arms.

Brief description notes for [Fig.3b]:

• It is very clear that all 3 spirals are real polyspirals starting in the center.
• The third image shows how spiral arms are plotted, which in turn explains why we are seeing them: the distances between dots in the spiral arms is much less than a length of related line fragments in a polyspiral. So, our brain is telling us: "Hey, look - these are 9 spiral arms (in [Fig.3a/3])!" And we would agree.

The [Fig.4a] is similar to the [Fig.3a], but all spiral arms have opposite direction, i.e., counterclockwise.

It is now very clear that all 3 spirals in [Fig.4b] are real polyspirals starting in the center.

The [Fig.5a] is similar to the [Fig.3a], except for the central area.

It is very clear that all 3 spirals in [Fig.5b] are real polyspirals starting in the center.

Brief description notes for [Fig.6a]:

• Did you notice that the first spiral here has very similar pattern to the canonical Vogel spiral [Fig.1a/1]? I.e., it has many visible clockwise and counterclockwise secondary spiral arms, but no dense seeds in the central area.
• I think it matches real natural sunflower seed pattern even more precisely. Especially, because there is no seeds in the central area of a real sunflower. What do you think?
  I'm just teasing real experts in this subject, because I'm not even close to conducting such botanical analysis.

It is very clear that both 2nd and 3rd spirals in [Fig.6b] are real polyspirals starting in the center. If so, - then the 1st spiral is a polyspiral too.

In addition, the third spiral shows you how the secondary 3 spiral arms are formed from overlapping line segments.

Using the sample webpages

A few webpages are attached in the zip-file: "VogelSpiral", "VogelSpiral2", and "VogelSpiral3". The first two pages are using default set of parameters .

The first page generates and plots Vogel spirals in dots or lines (see results in [Fig.1a,b - Fig.6a,b]).

The second page plots spirals using both dots and lines (see results in [Fig.1b - Fig.6b])

The third page is a modified version of the "Spiral generator" page from [11]. It allows user to see how close are Vogel spirals plotted using different initial angles. This is possible because it allows to plot one spiral over another using different colors.

If you want to see the full range of Vogel spirals, you can use "VogelSpiral3". Find already tested samples in the Table 1 below. Try them first. Then find your own favorite samples.

Notes about Table 1:

• Init angle 'it' in the 2nd column shows a starting initial angle it.
• Scale in the 4th column shows an additional scaling parameter, which allows user to speed-up testing for a very big initial angles it. E.g., the sample #2 has an initial angle bigger than 41K degrees.
• P/O shows plotting mode: 'P' stands for initial plotting (with cleaning canvas); 'O' stands for plotting over already plotted spiral(s).

Table 1. Testing samples

#	Init angle 'it'	Dots	Scale	Color	P/O	Notes
1	0.1	256	1.0	darkgreen	P	smooth spiral
2	7.138	256	103.0	darkgreen	P	pure spiral again
3	2.399963	256	1.0	darkgreen	P	canonical Vogel spiral
4	2.4	256	1.0	red	O	almost the same [added 0.0001 to 'it']
5	2.401	256	1.0	yellow	O	almost the same [added 0.001 to 'it']
6	2.5	256	1.0	navy	P	diff. pattern
7	7.13	256	1.0	navy	P	same pattern
8	7.134	256	1.0	navy	P	same pattern
9	7.135	256	1.0	navy	P	same pattern
10	7.136	256	1.0	navy	P	same pattern
11	2.399963	256	2.0	maroon	P	same pattern
12	2.399963	256	3.0	maroon	P	same pattern
13	2.6	256	1.0	red	P	same pattern
14	2.7	256	1.0	red	P	diff. pattern
15	2.9	256	1.0	red	P	diff. pattern
16	3.0	256	1.0	red	P	same pattern
17	3.3	256	1.0	red	P	same pattern
18	3.4	256	1.0	red	P	same pattern
19	5.3	256	1.0	red	O	same pattern

If you will continue testing, - then soon you will discover thousands of differently (and similarly) looking spirals.

• Changing the initial "golden" angle (an irrational number, dark green dots) by +0.0001 radians (now a rational number, red dots) almost not effected the resultant spiral. Actually, if a color would be the same, - the difference can't be detected with a "naked" eye. In [Fig.7] you can see overlapping dark green and red dots mostly closer to the canvas edges.
• Adding an additional 0.001 to the initial angle (a rational number, yellow dots) changed this spiral a little bit. But still this spiral has almost the same pattern, i.e., many visible clockwise and counterclockwise secondary spiral arms.
• Many other samples from the Table 1 (#7-#19) are producing patterns close to the canonical Vogel spiral too.
• Also, try to vary number of dots to see different patterns. It happens, because of default scaling used in canvas plotting.
• #6: the different pattern, only c-c-w arms are notable;
• #7: the same pattern, but c-w arms are more notable;
• #8-#10: the same pattern, but c-c-w arms are more and more notable;
• #11: actually, still the same pattern, but c-c-w arms are more notable;
• #12: almost the same pattern, but c-w arms are more notable;
• #13: almost the same pattern, but c-c-w arms are more notable near the center;
• #14: the different pattern, only c-w arms are notable;
• #15: the different pattern, only c-c-w arms are notable (near the center);
• #16: almost the same pattern, but c-c-w arms are more notable near, plus a different center;
• #17: almost the same as #15.
• #18: almost the same as #16.
• #19: almost the same as #3, just plot it after #3. Try it=1.7 to compare
• Try also the following it: 0.2, 0.5, 1.0, 1.1, 1.2, 1.5, 1.9, 2.0, 2.23, 2.27, 2.3. And so on...

Conclusion

In [6,10] and in a few other articles authors discussed what to select as initial angle: rational or irrational number?

Actually, the difference between rational and irrational numbers is very tiny. Thus, statements about requirements for angle to be the irrational is incorrect. In fact, many rational numbers can produce the same pattern, at least very close to canonical Vogel spiral (see [Fig.7] below).

The [Fig.7] was plotted using "Vogel3" page and Table 1 samples: #3, #4 and #5. It is very clear now:

• Changing the initial "golden" angle (irrational number, dark green dots) by +0.0001 radians (now rational number, red dots) almost not effected resultant spiral. Actually, if color would be the same, - the difference can't be detected with "naked" eye. In [Fig.7] you can see overlapping dark green and red dots mostly closer to the edges of canvas.
• Adding additional 0.001 to the initial angle (rational number, yellow dots) changed Vogel spiral a little bit. But still spiral has almost the same pattern, i.e., many visible clockwise and counterclockwise secondary spiral arms.
• Many other samples from the Table 1 (#7-#19) are producing patterns close to canonical Vogel spiral too.

Hmm... may be 137.507 degrees angle is not so "golden" in this case?!

• First, the starting "canonical" Vogel spiral in [Fig. 1a] is very popular and presented both in [5-7] (and in many other articles), but authors still haven't linked it to the lucky coincident of using very big golden angle and plotting big dots. We are grateful to H. Vogel for discovering this amazing pattern. If he and other authors would use lines for plotting (even using golden angle), they would never see this pattern. Authors were studying a sunflower seed pattern, so, the logical choice was to use big dots. And it helped.
• Second, what is the most important to produce a desired pattern is the following set of units and parameters defined by H. Vogel for capitulum:
  • big dots (not line segments);
  • an initial big angle and a method of its increasing (tiny angle is producing smooth spiral, using even bigger angle works too, e.g., look at [Fig.6a/1]);
  • a number of dots (a small number is not producing a desired pattern, but a very big number is able to do it, e.g., look at [Fig.6a/1]);
  • the unique function, i.e., the Vogel's function.

It should be stressed, that in [9] was mentioned the following:

This is the correct point of view, but the next one is only partially correct [9]:

Note: they are talking about real, visible secondary spiral arms.

Stating that "no such spirals are there" is incorrect. Spirals (spiral arms) are there! They are real! You can plot them manually. What is correct is the rest of statement, i.e., "it is one’s vision that is creating the radial spirals." But this is correct only in the context of knowing that whole image is a spiral.

So, they still didn't link this visible pattern to the lucky coincident of using golden angle and plotting big dots.

I think it would be very interesting if somebody would tell us why some angle can trick our vision and brain. I mean, to point us to more precise explanation than mine, if any.

May be, when we are looking at the pictures of the spiral galaxy, we are tricked too? I.e.: instead of seeing billion of orbiting the central black hole stars we are having picture of these stars arranged in the spiral arms. The reason is the same: we can't see the elliptic orbits, because the distance between them is tiny, and each star has its own one. Instead, we have a snapshot of all stars looking as spiral arms. Note: not all galaxies are having spiral arms. Majority of them are looking as disks, and this may supports this hypothesis.

References

1. Spiral, Wikipedia, the free encyclopedia, URL: https://en.wikipedia.org/wiki/Spiral.
2. Polyspiral, Rosetta Code Wiki, URL: http://rosettacode.org/wiki/Polyspiral.
3. Polar coordinate system, Wikipedia, the free encyclopedia, URL: https://en.wikipedia.org/wiki/Polar_coordinate_system.
4. Wassenaar, J. Mathematical curves, URL: http://www.2dcurves.com/spiral/spiral.html
5. Vogel, H (1979). A better way to construct the sunflower head. Mathematical Biosciences. 44 (44): pp. 179-189. doi:10.1016/0025-5564(79)90080-4.
6. Prusinkiewicz, P.; Lindenmayer, A (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101-107. ISBN 978-0-387-97297-8.
7. Mathai, A.M.; Davis, T.A. (1974) Constructing the sunflower head, Mathematical Biosciences, 20, 117-133. doi: 10.1016/0025-5564(74)90072-8.
8. Bonnet, C.(1754) Recherches sur I’usage des feuilies akns les p/antes, Gottingen and Leiden.
9. Haubold, H.J; Mathai, A.M. (2015) Scientific Endeavors of A.M. Mathai: An Appraisal on the Occasion of his Eightieth Birthday. URL: https://arxiv.org/pdf/1502.07382.pdf
10. Devert, A. Spreading points on a disc and on a sphere. URL: http://blog.marmakoide.org/?p=1.
11. Voevudko, A.E. (2017) Dancing with Spirals. Code Project, URL: https://www.codeproject.com/Articles/1213518/Dancing-with-Spirals.

History

12/17/2017 Updating "Conclusion" upon requests from a few friends. Adding "History". Plus a few short edits
12/15/2017 Initial posting.