Solving the Pentominoes problem using C# and Bit-wise Operations

• Download source - 17.3 KB

Introduction

This problem can be viewed as solving a jigsaw puzzle with twelve pieces. Sounds simple enough, doesn't it?

There are twelve differently shaped pieces called pentominoes (c.f, dominoes). They are tiles comprised of five squares joined along their edges in different configurations. Each tile looks vaguely like a letter, so they are uniquly identified by that letter. The challenge is to arrange the tiles in rectangular grids of 60 squares. The possible grid sizes are 6x10, 5x12, 4x15 and 3x20. This project solves the challenge by using 64-bit long unsigned integers to represent the board and the individual tiles in each orientation. This representation reduces the problem of determing whether a tile fits the current board to a bit-wise OR operation and a bit-wise XOR operation. The program demonstrates that using bit-wise operations can dramatically simplify and speed up some computing problems.

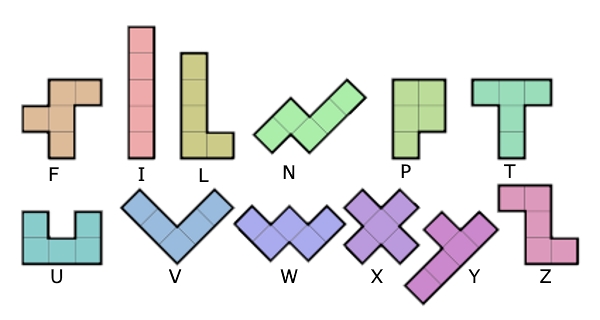
Image: Wikimedia Commons

Background

I was inspired to develop this program after reading an article on Pentominoes at the Futility Closet website. I read that Arthur C. Clarke had "calculated that solving the problem by blind permutation would take more than 20 billion years." That seemed high and I figured the answer was more like 7000 years at one move per second (12! x 8 orientations x 60 board positions). Still, it seemed like a simple problem to solve using a brute-force computer program. All I needed was a two dimensional array of bytes and some method for filling it up with a set of 12 smaller arrays with occupied and unoccupied cells. A couple of inconclusive tests that ran all night without finding a result suggested I needed to rethink my approach. My answer was to map the problem space into bit-wise operations on 64-bit words.

Running the Program

The user interface is a simple Windows form. You can select the board size and whether or not the initial order of tiles should be shuffled. Because there are multiple solutions, the order in which tiles are tried affects the solution. I could have iterated through all possible solutions (2339 for the 6x10 grid, 1010 for the 5x12 grid, 368 for the 4x15 and 2 for rhe 3x20 grid), but then I'd have to figure out a nice way to show 3719 differents solutions.

After you choose the Grid Dimensions, you can click the Solve button and see the first solution found using the initial tile order, which is L, F, I, N, P, T, U, V, W, X, Y, Z. If you checked

Randomize order of tiles

, then you would probably see a different solution.

A solution for a 6x10 grid
 

A solution for a 5x12 grid
 

A solution for a 4x15 grid
 

One solution for a 3x20 grid
 

The other solution for a 3x20 grid
 

Using the code

The solution is a standard Visual Studio 2017 Windows Form application written in C#. The solution should open in that version of Visual Studio or later versions.

Points of Interest

Binary Representation of the board and tiles

I initially tried solving the problem using two dimensional byte arrays. That became very cumbersome very quickly. The hardest problem was figuring out which potential moves should be accepted and which should be rejected. Then I realized that I could map the board and tiles to 64-bit integers and use bit-wise operations such as & (and), | (or), ^ (xor), >> (shift right) and << (shift left) to place pieces in different positions. That reduced iterating through sixty board positions and a 5x5 array that represented a tile to two machine level operations on 64-bit words.

The 5x10 board can be represented as a grid. The example below shows the T tile placed on the board.

If we represent this board as 60 binary digits, with occupied squares set to 1 and empty squares set to 0, we get the following bit string. The final four bits are outside the board. For convenience, we can set them to 1.

011100000000100000000010000000000000000000000000001111

This also tells us how to represent the T tile as a binary number at position 1. If want to move the T tile to the right by one position, all we need to do is use a right shift operation, and we will have the binary representation of T at position 2. We can thus move the T to any position on the board. We do have to have some tests to ensure that we ignore positions where the T overflows the board. Thus, the valid binary representations of the T tile at each position on a 5x12 board, with obvious entries omitted, are:

0  11100000000001000000000001
1  011100000000001000000000001
2  0011100000000001000000000001
and so on...
8  0000000011100000000001000000000001
9  0000000001110000000000100000000000
skip overflow
12 00000000000011100000000001000000000001
13 000000000000011100000000001000000000001
and so on...
20 0000000000000000000011100000000001000000000001
21 00000000000000000000011100000000001000000000001
skip overflow
24 00000000000000000000000011100000000001000000000001
25 000000000000000000000000011100000000001000000000001
and so on
32 0000000000000000000000000000000011100000000001000000000001
33 00000000000000000000000000000000011100000000001000000000001
skip overflow

After we have placed some other tiles on the board, the board might look like this.

If we convert the board to a binary number, where 1 is occupied and 0 is unoccupied, then we get the following binary number. I broke it into five twelve digit binary numbers for clarity and then strung them together,:

100000000000
110000000000
110100000000
111100000000
111110000000

100000000000110000000000110100000000111100000000111110000000

So now we want to see where the T tile can be fitted. Take the T at position 0 and the board as binary digits and apply the Or and Xor operator to the pair.

Board:  100000000000110000000000110100000000111100000000111110000000
T tile: 11100000000001000000000001
Or:     111000000000110000000000110100000000111100000000111110000000
Xor:    011000000000100000000100100100000000111100000000111110000000

Now try the same two operations with the T tile at position 1.

Board:  100000000000110000000000110100000000111100000000111110000000
T tile: 011100000000001000000000001
Or:     111100000000111000000000101100000000111100000000111110000000
Xor:    111100000000111000000000101100000000111100000000111110000000

In the case of position 1, we can see that the results of the Or and Xor operations between the tile piece and the board are the same. This indicates that all parts of the tile filled empty squares on the board and there were no collisions with occupied squares, i.e. position 1 is a valid position for the T tile. The result of the Or operation becomes the board for the next tile.

By using bit-wise operations we have simplified testing whether a tile can be placed on the board, and where, to three basic machine operations - Shift, Or and Xor. Note that the number of 1-bit shift operations corresponds to the board position of the upper left square of the tile.

Representing Tiles

The tiles can be rotated, so we actually need four different bit maps for each tile. If we allow them to be flipped, then we would need eight. As it turned out, four is sufficent, with one proviso for the 3x20 solution, noted below. The following enum and object is used to represent each tile.

public enum Rotation
{
   zero,
   ninety,
   one80,
   two70,
   undefined
}

public class Tile
{
   public int Number { get; set; }
   public string Letter { get; set; }
   public int Placed { get; set; }
   public Rotation Rotation { get; set; }
   public int Shift { get; set; }
   public byte[,] Slots;
   public ulong?[] BitMap = new ulong?[4];   // indexed by Rotation
   public int[] TileWidth = new int[4];      // indexed by Rotation, used to check for Board overflow
   public Tile(int number)
   {
      this.Placed = -1;
      this.Rotation = Rotation.undefined;
      this.Number = number;
   }
}

The ulong?[] BitMap property holds the binary representation of the tile while the byte[,] Slots property holds a two dimensional representation. For convenience, we populate the Slots and then create a Bitmap for each Rotation. The following code is used to intialize the T tile.

_Tiles[9].Slots = new byte[3, 3] { { 1, 1, 1 }, { 0, 1, 0 }, { 0, 1, 0 } };
_Tiles[9].Letter = "T";

The following code is used to rotate the Slots array, strip out empty rows, populate the Bitmap and set the Tilewidth.

slots = Rotate(_Tiles[i].Slots, Rotation.one80);
_Tiles[i].TileWidth[(int)Rotation.one80] = slots.GetUpperBound(1) + 1;
_Tiles[i].BitMap[(int)Rotation.one80] = slots.ToBitMap(_Width, _Height);

public byte[,] Rotate(byte[,] slots, Rotation r)
{
   byte[,] rotSlots = null;
   int rowMax = slots.GetUpperBound(0);
   int colMax = slots.GetUpperBound(1);
   switch (r) {
      case Rotation.zero:
         rotSlots = slots;
         break;
      case Rotation.ninety:
         rotSlots = new byte[colMax + 1, rowMax + 1];
         for (int col = 0; col <= colMax; col++) {
            for (int row = 0; row <= rowMax; row++) {
               rotSlots[col, rowMax - row] = slots[row, col];
            }
         }
         break;
      case Rotation.one80:
         rotSlots = new byte[rowMax + 1, colMax + 1];
         for (int col = 0; col <= colMax; col++) {
            for (int row = 0; row <= rowMax; row++) {
               rotSlots[rowMax - row, colMax - col] = slots[row, col];
            }
         }
         break;
      case Rotation.two70:
         rotSlots = new byte[colMax + 1, rowMax + 1];
         for (int col = 0; col <= colMax; col++) {
            for (int row = 0; row <= rowMax; row++) {
               rotSlots[colMax - col, row] = slots[row, col];
            }
         }
         break;
   }
   return StripEmptyRowsAndColumns(rotSlots);
}

public static ulong? ToBitMap(this byte[,] byteMap, int width, int height)
{
   ulong? result = 0;
   int bitPos = 63;
   int rows = byteMap.GetUpperBound(0) + 1;
   if (rows > height) {
      return null;
   }
   for (int row = 0; row <= byteMap.GetUpperBound(0); row++) {
      for (int col = 0; col <= byteMap.GetUpperBound(1); col++) {
         if (byteMap[row, col] == 1) {
            result = SetBit(result, bitPos);
         }
         bitPos--;
      }
      bitPos = 63 - width * (row + 1);
   }
   return result;
}

 private static ulong? SetBit(ulong? value, int index)
 {
    if (index < 0 || index >= 64) {
       throw new ArgumentOutOfRangeException();
    }
    ulong? one = 1;

    return value | (one << index);
}

Laying the tiles

The puzzle is solved by the following recursive method.

public StatusFlag TilePlaced(ulong board, int level)
{
   // Increment to next level of recursion
   level++;
   if (level > _Tiles.Count) {
      return StatusFlag.Failed;
   }
   // Reset tiles placed at higher levels of recursion
   for (int tileX = 0; tileX < _Tiles.Count; tileX++) {
      if (_Tiles[tileX].Placed >= level) {
         _Tiles[tileX].Placed = -1;
      }
   }
   // Iterate through tiles
   for (int x = 0; x < _Tiles.Count; x++) {
      // Choose shuffled tile ordinal
      int tileX = _Order[x];
      // Skip placed tiles
      if (_Tiles[tileX].Placed != -1 && _Tiles[tileX].Placed < level) {
         continue;
      }
      _Tiles[tileX].Placed = -1;
      // Iterarate through rotation
      for (Rotation rotation = Rotation.zero; rotation <= Rotation.two70; rotation++) {
         // Get pice as ulong
         ulong? nullablePiece = _Tiles[tileX].BitMap[(int)rotation];
         if (nullablePiece != null) {
            ulong basePiece = nullablePiece.Value;
            ulong piece = basePiece;
            int tileWidth = _Tiles[tileX].TileWidth[(int)rotation];
            // Iterate through all possible board positions by shifting
            for (int shift = 0; shift < _Width * _Height; shift++) {
               // Break when last bit is going to be shifted away
               if ((piece >> 4) % 2 == 1) {
                  break;
               }
               // Move the piece by shiftind
               piece = basePiece >> shift;
               // Skip if shift position invalid (i.e overflows board)
               if (SkipShift(shift, tileWidth)) {
                  continue;
               }
               // OR the piece and board
               ulong b = board | piece;
               // Test if result matches XOR of piece and board
               if (b == (board ^ piece)) {
                  // Optimization - ensure Tile placement leaves no holes that can't be filled
                  if (b.NoHoles(_Width, _Height)) {
                     // Place tile
                     _Tiles[tileX].Placed = level;
                     _Tiles[tileX].Shift = shift;
                     _Tiles[tileX].Rotation = rotation;
                     _Counter++;
                     // Test for completion
                     if (level >= _Tiles.Count && b == _CompletedBoard) {
                        ReDrawAllCells(picBoard, level);
                        ReportSolved();
                        return StatusFlag.Finished;
                     }
                     // Recurse with new board
                     StatusFlag statusFlag = TilePlaced(b, level);
                     if (statusFlag != StatusFlag.Failed) {
                        return statusFlag;
                     }
                     else {
                        // Failed after recursion - continue iterations
                        _Tiles[tileX].Placed = -1;
                        continue;
                     }
                  }
               }
            }
         }
      }
   }
   return StatusFlag.Failed;
}

Optimization

While the puzzle could be solved by trying all possible combinations, it is better to try the way a human would solve the puzzle. That is to start at one corner and try to fit pieces together without leaving gaps that can't be filled. The extension method NoHoles does that. It basically ensures that a non-empty row can only start with a sequence of binary 1s. In effect, the program tries to fill the board from right to left

Display Considerations

The list of twelve tiles represented by the Tile object provides the information needed to display the board and tiles on the form. After a solution is found, the program displays the tiles in left to right order of final placement, with a small time interval between each tile display.

Using the Bit Array Class instead of 64-bit words

One alternative to using actual bit representations for the board and tiles would be to use the .Net frameworks's BitArray class. I started to create a version of the project to use this class. I stopped when I discovered that the bit array class had no native shift methods.