- Code that accompanies this article can be downloaded here.
Sometime in the last few weeks, while I was writing the explanations for the way in which neural networks learn and backpropagation algorithm, I realized how I never tried to implement these algorithms in one of the programming languages. Then it struck me that I’ve never tried to implement the whole Artificial Neural Network from scratch. I was always using some libraries that were hiding that implementation from me so I could focus on the mathematical model and the problem I was trying to solve. One thing led to another and the decision to implement my own Neural Network from scratch without using third-party libraries was made. Also, I decided to use the object-oriented programming language I prefer – C#.
This means that a more OO approach was taken and not the usual scripting point of view like we would have by using Python and R. One very good article did that implementation that kind of way and I strongly recommend you to skim through it. What I wanted to do is to separate every component and every operation. What was initially just a thought exercise grew into quite a cool mini side-project. So, I decided to share it with the world. Before we dive into the code, I would like to emphasize that this is not really the way you would generally implement the network. More math and forms of matrix multiplication should be used to optimize this entire process.
Apart from that, the implemented network represents a simplified, most basic form of Neural Network. Nevertheless, this way one can see all the components and elements of one Artificial Neural Network and get more familiar with the concepts from previous articles.
Artificial Neural Network Structure
Before we dive into the code, let’s run through the structure of ANN. In general, Artificial Neural Networks are biologically motivated, meaning that they are trying to mimic the behavior of the real nervous systems. Just like the smallest building unit in the real nervous system is the neuron, the same is with artificial neural networks – the smallest building unit is artificial neuron. In a real nervous system, these neurons are connected to each other by synapsis, which gives this entire system enormous processing power, ability to learn and huge flexibility. Artificial neural networks apply the same principle.
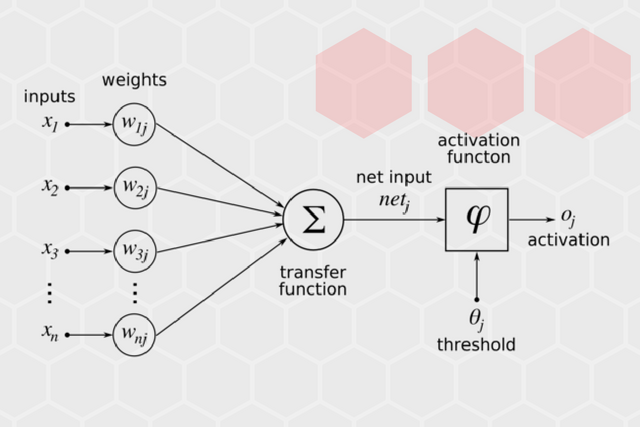
By connecting artificial neurons, they aim to create a similar system. They are grouping neurons into layers and then create connections among neurons from each layer. Also, by assigning weights to each connection, they are able to filter important from non-important connections. The structure of the artificial neuron is a mirroring structure of the real neuron, too. Since they can have multiple inputs, i.e., input connections, a special function that collects that data is used – input function. The function that is usually used as input function in neurons is the function that sums all weighted inputs that are active on input connections – weighted input function.
Another important part of each artificial neuron is activation function. This function defines whether this neuron will send any signal to its outputs and which value will be propagated to the outputs. Basically, this function receives value from the input function and according to this value it generates an output value and propagates them to the outputs.
Implementation
So, as you can see from the previous chapter, there are a few important entities that we need to pay attention to and that we can abstract. They are neurons, connections, layer, and functions. In this solution, a separate class will implement each of these entities. Then, by putting it all together and adding backpropagation algorithm on top of it, we will have our implementation of this simple neural network.
Input Functions
As mentioned before, crucial parts of the neuron are input function and activation function. Let’s examine the input function. First, I created an interface for this function so it can be easily changed in the neuron implementation later on:
public interface IInputFunction
{
double CalculateInput(List<ISynapse> inputs);
}
These functions have only one method – CalculateInput, which receives a list of connections which are described in ISynapse interface. We will cover this abstraction later; so far all we need to know is that this interface represents connections among neurons. CalculateInput method needs to return some sort of value based on the data contained in the list of connections. Then, I did the concrete implementation of input function – weighted sum function.
public class WeightedSumFunction : IInputFunction
{
public double CalculateInput(List<ISynapse> inputs)
{
return inputs.Select(x => x.Weight * x.GetOutput()).Sum();
}
}
This function sums weighted values on all connections that are passed in the list.
Activation Functions
Taking the same approach as in input function implementation, the interface for activation functions is implemented first:
public interface IActivationFunction
{
double CalculateOutput(double input);
}
After that, concrete implementations can be done. The CalculateOutput method should return the output value of the neuron based on input value that it got from input function. I like to have options, so I’ve done all functions mentioned in one of the previous blog posts. Here is how the step function looks:
public class StepActivationFunction : IActivationFunction
{
private double _treshold;
public StepActivationFunction(double treshold)
{
_treshold = treshold;
}
public double CalculateOutput(double input)
{
return Convert.ToDouble(input > _treshold);
}
}
Pretty straightforward, isn’t it? A threshold value is defined during the construction of the object, and then the CalculateOutput returns 1 if the input value exceeds the threshold value, otherwise, it returns 0.
Other functions are easy as well. Here is the Sigmoid activation function implementation:
public class SigmoidActivationFunction : IActivationFunction
{
private double _coeficient;
public SigmoidActivationFunction(double coeficient)
{
_coeficient = coeficient;
}
public double CalculateOutput(double input)
{
return (1 / (1 + Math.Exp(-input * _coeficient)));
}
}
And here is Rectifier activation function implementation:
public class RectifiedActivationFuncion : IActivationFunction
{
public double CalculateOutput(double input)
{
return Math.Max(0, input);
}
}
So far so good – we have implementations for input and activation function, and we can proceed to implement the trickier parts of the network – neurons and connections.
Neuron
The workflow that a neuron should follow goes like this: Receive input values from one or more weighted input connections. Collect those values, do some kind of processing, and pass them to the activation function, which calculates the output value of the neuron. Send those values to the outputs of the neuron. Based on that workflow abstraction of the neuron, this is created:
public interface INeuron
{
Guid Id { get; }
double PreviousPartialDerivate { get; set; }
List<ISynapse> Inputs { get; set; }
List<ISynapse> Outputs { get; set; }
void AddInputNeuron(INeuron inputNeuron);
void AddOutputNeuron(INeuron inputNeuron);
double CalculateOutput();
void AddInputSynapse(double inputValue);
void PushValueOnInput(double inputValue);
}
Before we explain each property and method, let’s see the concrete implementation of a neuron, since that will make the way it works far clearer:
public class Neuron : INeuron
{
private IActivationFunction _activationFunction;
private IInputFunction _inputFunction;
public List<ISynapse> Inputs { get; set; }
public List<ISynapse> Outputs { get; set; }
public Guid Id { get; private set; }
public double PreviousPartialDerivate { get; set; }
public Neuron(IActivationFunction activationFunction, IInputFunction inputFunction)
{
Id = Guid.NewGuid();
Inputs = new List<ISynapse>();
Outputs = new List<ISynapse>();
_activationFunction = activationFunction;
_inputFunction = inputFunction;
}
public void AddInputNeuron(INeuron inputNeuron)
{
var synapse = new Synapse(inputNeuron, this);
Inputs.Add(synapse);
inputNeuron.Outputs.Add(synapse);
}
public void AddOutputNeuron(INeuron outputNeuron)
{
var synapse = new Synapse(this, outputNeuron);
Outputs.Add(synapse);
outputNeuron.Inputs.Add(synapse);
}
public double CalculateOutput()
{
return _activationFunction.CalculateOutput(_inputFunction.CalculateInput(this.Inputs));
}
public void AddInputSynapse(double inputValue)
{
var inputSynapse = new InputSynapse(this, inputValue);
Inputs.Add(inputSynapse);
}
public void PushValueOnInput(double inputValue)
{
((InputSynapse)Inputs.First()).Output = inputValue;
}
}
Each neuron has its unique identifier – Id. This property is used in backpropagation algorithm later. Another property that is added for backpropagation purposes is the PreviousPartialDerivate, but this will be examined in detail further on. A neuron has two lists, one for input connections – Inputs, and another one for output connections – Outputs. Also, it has two fields, one for each of the functions described in previous chapters. They are initialized through the constructor. This way, neurons with different input and activation functions can be created.
This class has some interesting methods, too. AddInputNeuron and AddOutputNeuron are used to create a connection among neurons. The first one adds input connection to some neuron and the second one adds output connection to some neuron. AddInputSynapse adds InputSynapse to the neuron, which is a special type of connection. These are special connections that are used just for the input layer of the neuron, i.e., they are used only for adding input to the entirety of the system. This will be covered in more detail in the next chapter.
Last but not least, the CalculateOutput method is used to activate a chain reaction of output calculation. What will happen when this function is called? Well, this will call input function, which will request values from all input connections. In turn, these connections will request output values from input neurons of these connections, i.e., output values of neurons from the previous layer. This process will be done until input layer is reached and input values are propagated through the system.
Connections
Connections are abstracted through ISynapse interface:
public interface ISynapse
{
double Weight { get; set; }
double PreviousWeight { get; set; }
double GetOutput();
bool IsFromNeuron(Guid fromNeuronId);
void UpdateWeight(double learningRate, double delta);
}
Every connection has its weight represented through the property of the same name. Additional property PreviousWeight is added and it is used during backpropagation of the error through the system. Update of the current weight and storing of the previous one is done in helper function UpdateWeight. There is another helper function – IsFromNeuron, which detects if a certain neuron is an input neuron to the connection. Of course, there is a method that gets an output value of the connection – GetOutput.
Here is the implementation of the connection:
public class Synapse : ISynapse
{
internal INeuron _fromNeuron;
internal INeuron _toNeuron;
public double Weight { get; set; }
public double PreviousWeight { get; set; }
public Synapse(INeuron fromNeuraon, INeuron toNeuron, double weight)
{
_fromNeuron = fromNeuraon;
_toNeuron = toNeuron;
Weight = weight;
PreviousWeight = 0;
}
public Synapse(INeuron fromNeuraon, INeuron toNeuron)
{
_fromNeuron = fromNeuraon;
_toNeuron = toNeuron;
var tmpRandom = new Random();
Weight = tmpRandom.NextDouble();
PreviousWeight = 0;
}
public double GetOutput()
{
return _fromNeuron.CalculateOutput();
}
public bool IsFromNeuron(Guid fromNeuronId)
{
return _fromNeuron.Id.Equals(fromNeuronId);
}
public void UpdateWeight(double learningRate, double delta)
{
PreviousWeight = Weight;
Weight += learningRate * delta;
}
}
Notice the fields _fromNeuron and _toNeuron, which define neurons that this synapse connects.
Apart from this implementation of the connection, there is another one that I’ve mentioned in the previous chapter about neurons. It is InputSynapse and it is used as an input to the system. The weight of these connections is always 1 and it is not updated during the training process. Here is the implementation of it:
public class InputSynapse : ISynapse
{
internal INeuron _toNeuron;
public double Weight { get; set; }
public double Output { get; set; }
public double PreviousWeight { get; set; }
public InputSynapse(INeuron toNeuron)
{
_toNeuron = toNeuron;
Weight = 1;
}
public InputSynapse(INeuron toNeuron, double output)
{
_toNeuron = toNeuron;
Output = output;
Weight = 1;
PreviousWeight = 1;
}
public double GetOutput()
{
return Output;
}
public bool IsFromNeuron(Guid fromNeuronId)
{
return false;
}
public void UpdateWeight(double learningRate, double delta)
{
throw new InvalidOperationException
("It is not allowed to call this method on Input Connection");
}
}
Layer
Implementation of the neural layer is quite easy:
public class NeuralLayer
{
public List<INeuron> Neurons;
public NeuralLayer()
{
Neurons = new List<INeuron>();
}
public void ConnectLayers(NeuralLayer inputLayer)
{
var combos = Neurons.SelectMany(neuron => inputLayer.Neurons,
(neuron, input) => new { neuron, input });
combos.ToList().ForEach(x => x.neuron.AddInputNeuron(x.input));
}
}
It contains the list of neurons used in that layer and the ConnectLayers method, which is used to glue two layers together.
Simple Artificial Neural Network
Now, let’s put all that together and add backpropagation to it. Take a look at the implementation of the Network itself:
public class SimpleNeuralNetwork
{
private NeuralLayerFactory _layerFactory;
internal List<NeuralLayer> _layers;
internal double _learningRate;
internal double[][] _expectedResult;
public SimpleNeuralNetwork(int numberOfInputNeurons)
{
_layers = new List<NeuralLayer>();
_layerFactory = new NeuralLayerFactory();
CreateInputLayer(numberOfInputNeurons);
_learningRate = 2.95;
}
public void AddLayer(NeuralLayer newLayer)
{
if (_layers.Any())
{
var lastLayer = _layers.Last();
newLayer.ConnectLayers(lastLayer);
}
_layers.Add(newLayer);
}
public void PushInputValues(double[] inputs)
{
_layers.First().Neurons.ForEach(x => x.PushValueOnInput
(inputs[_layers.First().Neurons.IndexOf(x)]));
}
public void PushExpectedValues(double[][] expectedOutputs)
{
_expectedResult = expectedOutputs;
}
public List<double> GetOutput()
{
var returnValue = new List<double>();
_layers.Last().Neurons.ForEach(neuron =>
{
returnValue.Add(neuron.CalculateOutput());
});
return returnValue;
}
public void Train(double[][] inputs, int numberOfEpochs)
{
double totalError = 0;
for(int i = 0; i < numberOfEpochs; i++)
{
for(int j = 0; j < inputs.GetLength(0); j ++)
{
PushInputValues(inputs[j]);
var outputs = new List<double>();
_layers.Last().Neurons.ForEach(x =>
{
outputs.Add(x.CalculateOutput());
});
totalError = CalculateTotalError(outputs, j);
HandleOutputLayer(j);
HandleHiddenLayers();
}
}
}
private void CreateInputLayer(int numberOfInputNeurons)
{
var inputLayer = _layerFactory.CreateNeuralLayer(numberOfInputNeurons,
new RectifiedActivationFuncion(), new WeightedSumFunction());
inputLayer.Neurons.ForEach(x => x.AddInputSynapse(0));
this.AddLayer(inputLayer);
}
private double CalculateTotalError(List<double> outputs, int row)
{
double totalError = 0;
outputs.ForEach(output =>
{
var error = Math.Pow(output - _expectedResult[row][outputs.IndexOf(output)], 2);
totalError += error;
});
return totalError;
}
private void HandleOutputLayer(int row)
{
_layers.Last().Neurons.ForEach(neuron =>
{
neuron.Inputs.ForEach(connection =>
{
var output = neuron.CalculateOutput();
var netInput = connection.GetOutput();
var expectedOutput = _expectedResult[row][_layers.Last().Neurons.IndexOf(neuron)];
var nodeDelta = (expectedOutput - output) * output * (1 - output);
var delta = -1 * netInput * nodeDelta;
connection.UpdateWeight(_learningRate, delta);
neuron.PreviousPartialDerivate = nodeDelta;
});
});
}
private void HandleHiddenLayers()
{
for (int k = _layers.Count - 2; k > 0; k--)
{
_layers[k].Neurons.ForEach(neuron =>
{
neuron.Inputs.ForEach(connection =>
{
var output = neuron.CalculateOutput();
var netInput = connection.GetOutput();
double sumPartial = 0;
_layers[k + 1].Neurons
.ForEach(outputNeuron =>
{
outputNeuron.Inputs.Where(i => i.IsFromNeuron(neuron.Id))
.ToList()
.ForEach(outConnection =>
{
sumPartial += outConnection.PreviousWeight *
outputNeuron.PreviousPartialDerivate;
});
});
var delta = -1 * netInput * sumPartial * output * (1 - output);
connection.UpdateWeight(_learningRate, delta);
});
});
}
}
}
This class contains a list of neural layers and a layer factory, a class that is used to create new layers. During construction of the object, initial input layer is added to the network. Other layers are added through the function AddLayer, which adds a passed layer on top of the current layer list. The GetOutput method will activate the output layer of the network, thus initiating a chain reaction through the network. Also, this class has a few helper methods such as PushExpectedValues, which is used to set desired values for the training set that will be passed during training, as well as PushInputValues, which is used to set certain input to the network.
The most important method of this class is the Train method. It receives the training set and the number of epochs. For each epoch, it runs the whole training set through the network. Then, the output is compared with desired output and functions HandleOutputLayer and HandleHiddenLayer are called. These functions implement backpropagation algorithm.
Typical Workflow
Typical workflow can be seen in one of the tests implemented in the code on the repository – Train_RuningTraining_NetworkIsTrained. It goes something like this:
var network = new SimpleNeuralNetwork(3);
var layerFactory = new NeuralLayerFactory();
network.AddLayer(layerFactory.CreateNeuralLayer(3, new RectifiedActivationFuncion(),
new WeightedSumFunction()));
network.AddLayer(layerFactory.CreateNeuralLayer(1, new SigmoidActivationFunction(0.7),
new WeightedSumFunction()));
network.PushExpectedValues(
new double[][] {
new double[] { 0 },
new double[] { 1 },
new double[] { 1 },
new double[] { 0 },
new double[] { 1 },
new double[] { 0 },
new double[] { 0 },
});
network.Train(
new double[][] {
new double[] { 150, 2, 0 },
new double[] { 1002, 56, 1 },
new double[] { 1060, 59, 1 },
new double[] { 200, 3, 0 },
new double[] { 300, 3, 1 },
new double[] { 120, 1, 0 },
new double[] { 80, 1, 0 },
}, 10000);
network.PushInputValues(new double[] { 1054, 54, 1 });
var outputs = network.GetOutput();
Firstly, a neural network object is created. In the constructor, it is defined that there will be three neurons in the input layer. After that, two layers are added using function AddLayer and layer factory. For each layer, the number of neurons and functions for each neuron are defined. After this part is completed, the expected outputs are defined and the Train function with input training set and the number of epochs is called.
Conclusion
This implementation of the neural network is far from optimal. You will notice plenty of nested for loops which certainly have bad performance. Also, in order to simplify this solution, some of the components of the neural network were not introduced in this first iteration of implementation, momentum and bias, for example. Nevertheless, it was not a goal to implement a network with high performance, but to analyze and display important elements and abstractions that each Artificial Neural Network have.
Thanks for reading!
