Contents
Finding items of interest to user, based on those of other users of similar taste.
A collaborative filtering algorithm usually works by searching a large group of people and finding a smaller set with tastes similar to yours.
It looks at other things they like and combines them to create a ranked list of suggestions.
The underlying assumption is that if a person A has the same opinion as a person B on an issue, A is more likely to have B's opinion on a different issue than that of a randomly chosen person.
The dataset we are working with is a text file with the following headers
# Day, Action, UserID, UserName, ArticleID, ArticleName
We need to transform that into a matrix of users and their preferences.
@Override
public Map<Integer, Map<Integer, Double>> getUsersArticlesRatings(List<UserAction> userActions) {
Map<Integer, List<UserAction>> usersActions = userActions
.stream()
.collect(groupingBy(UserAction::getUserId));
Map<Integer, Map<Integer, Double>> usersArticlesRatings = new HashMap<>(usersActions.size());
for (Map.Entry<Integer, List<UserAction>> entry : usersActions.entrySet()) {
final Map<Integer, Double> articlesRatings = entry
.getValue()
.stream()
.collect(groupingBy(UserAction::getArticleId, ratingCalculator.getCollector()));
usersArticlesRatings.put(entry.getKey(), articlesRatings);
}
return usersArticlesRatings;
}
User actions can either be View, DownVote, UpVote or Download.
No matter how preferences are expressed, we need a way to map them onto numerical values.
public class RatingCalculatorImpl implements RatingCalculator {
private static Map<Action, Double> ACTION_WEIGHTS;
static {
ACTION_WEIGHTS = new HashMap<>();
ACTION_WEIGHTS.put(Action.View, 1d);
ACTION_WEIGHTS.put(Action.UpVote, 1d);
ACTION_WEIGHTS.put(Action.DownVote, -1d);
ACTION_WEIGHTS.put(Action.Download, 2d);
}
@Override
public Collector<UserAction, ?, Double> getCollector() {
return summingDouble(value -> ACTION_WEIGHTS.get(value.getAction()));
}
}
After collecting data about the things people like, we need a way to determine how similar people are in their tastes. We do this by comparing each person with every other person and calculating a similarity score.
We will use Pearson correlation coefficient, it is a measure of the linear correlation between two variables X and Y, or how well two sets of data fit on a straight line.
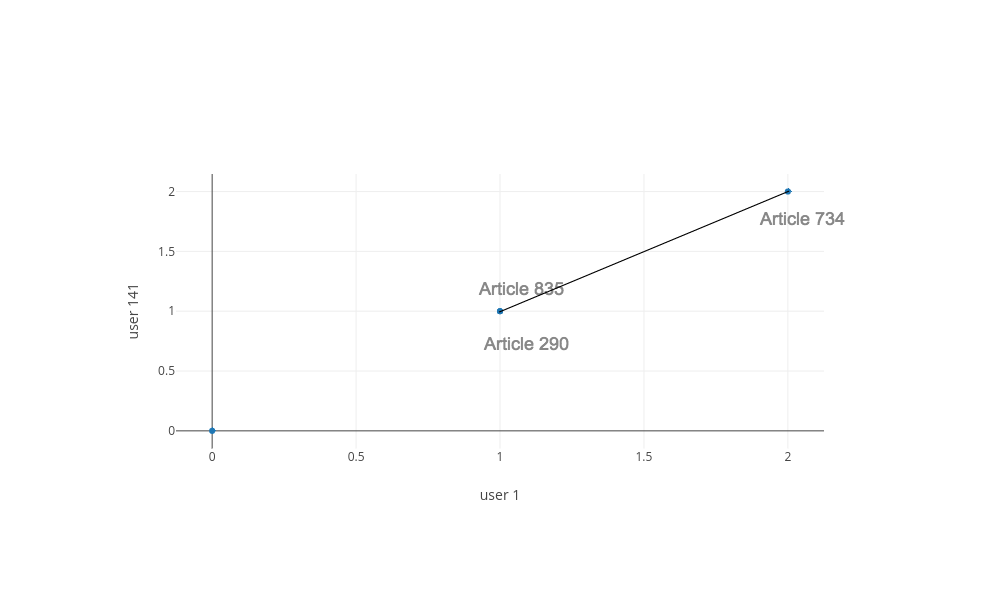
Visualization, the ratings of 3 articles read by both user 1 and user 141 make a straight line, correlation is 1.0
public class SimilarityCalculatorPearsonCorrelation implements SimilarityCalculator {
@Override
public double calculateScore(Map<Integer, Double> firstUserPreferences,
Map<Integer, Double> secondUserPreferences) {
List<Integer> commonArticles = getCommonArticles(firstUserPreferences.keySet(),
secondUserPreferences.keySet());
if (commonArticles.isEmpty()) {
return 0;
}
double sum1 = 0, sum2 = 0;
double sumSq1 = 0, sumSq2 = 0;
double sumProduct = 0;
for (Integer articleId : commonArticles) {
final Double user1Rating = firstUserPreferences.get(articleId);
final Double user2Rating = secondUserPreferences.get(articleId);
sum1 += user1Rating;
sum2 += user2Rating;
sumSq1 += Math.pow(user1Rating, 2);
sumSq2 += Math.pow(user2Rating, 2);
final double product = user1Rating * user2Rating;
sumProduct += product;
}
int n = commonArticles.size();
double num = sumProduct - (sum1 * sum2 / n);
double den = Math.sqrt((sumSq1 - Math.pow(sum1, 2) / n) * (sumSq2 - Math.pow(sum2, 2) / n));
if (den == 0) {
return 0;
}
return num / den;
}
private List<Integer> getCommonArticles(Set<Integer> firstUserPreferences,
Set<Integer> secondUserPreferences) {
List<Integer> commonArticles = new ArrayList<>();
for (Integer entry : firstUserPreferences) {
if (secondUserPreferences.contains(entry)) {
commonArticles.add(entry);
}
}
return commonArticles;
}
}
Now we can use the similarity score to caculate other users' taste compared to a given user.
private List<Recommendation> createScoreMatrix(int userId, Map<Integer, Map<Integer, Double>> matrix) {
Map<Integer, Double> userPreferences = matrix.get(userId) == null ?
new HashMap<>() : matrix.get(userId);
List<Recommendation> recommendations = new ArrayList<>(matrix.size());
for (Map.Entry<Integer, Map<Integer, Double>> entry : matrix.entrySet()) {
final Integer otherUserId = entry.getKey();
if (otherUserId == userId) {
continue;
}
final Map<Integer, Double> otherUserPreferences = matrix.get(otherUserId);
final double sim = similarityCalculator.calculateScore(userPreferences, otherUserPreferences);
if (sim > 0) {
final Map<Integer, Double> preferences = otherUserPreferences
.entrySet()
.stream()
.filter(e -> !userPreferences.containsKey(e.getKey()))
.collect(Collectors.toMap(p -> p.getKey(), p -> p.getValue()));
final Recommendation recommendation = new Recommendation(otherUserId, sim, preferences);
recommendations.add(recommendation);
}
}
return recommendations;
}
Using the similarity score, one might be tempted to rank top n users with similar taste and look for articles he hasn't viewed yet, but such an approach could accidentally turn up reviewers who haven’t reviewed some of the articles that he might like.
We need to score the articles by producing a weighted score that ranks the users. Take the votes of all the other users and multiply how similar they are to a given user by the score they gave each article.

This table shows correlation scores for each user and the ratings they gave the three articles (760, 9, and 514) that user 1 hasn't rated. The columns beginning with S.x give the similarity multiplied by the rating, so a person who is similar to user 1 will contribute more to the overall score than a person who is different. The Total row shows the sum of all these numbers.
We could just use the totals to calculate the rankings, but then an article reviewed by more users would have a big advantage. To correct for this, we need to divide by the sum of all the similarities for critics that reviewed that movie (the Sim. Sum row in the table).
private Map<Integer, WeightedScore> createWeightedScore(List<Recommendation> scoreMatrix) {
Map<Integer, WeightedScore> totalRatings = new HashMap<>();
scoreMatrix
.forEach(recommendation -> recommendation
.getOtherUserPreferences()
.forEach((articleId, rating) -> {
if (!totalRatings.containsKey(articleId)) {
totalRatings.put(articleId, new WeightedScore(0d, 0d));
}
final WeightedScore weightedScore = totalRatings.get(articleId);
final double total = weightedScore.getRatingSum() + rating;
weightedScore.setRatingSum(total);
if (recommendation.otherUserPreferences.containsKey(articleId)) {
weightedScore.setSimSum(weightedScore.getSimSum() +
recommendation.getSimilarity());
}
totalRatings.put(articleId, weightedScore);
}));
return totalRatings;
}
Now user 1 recommendations are:
Article Id, Rating
875:5.0
48:4.0
182:4.0
2427:4.0
483:4.0
We get a list of recommended articles & a predicted score of how user 1 will rate them.
