Subsurfer is a 3D modeling application written in JavaScript using the HTML5 Canvas control and WebGL. It implements the Catmull-Clark subdivision surface algorithm. A unique feature of the program is that the editing window implements 3D projection in a 2D canvas context using custom JavaScript code. The view window uses a 3D canvas context which is WebGL. Subsurfer was written in Notepad++ and debugged in Chrome.
Introduction
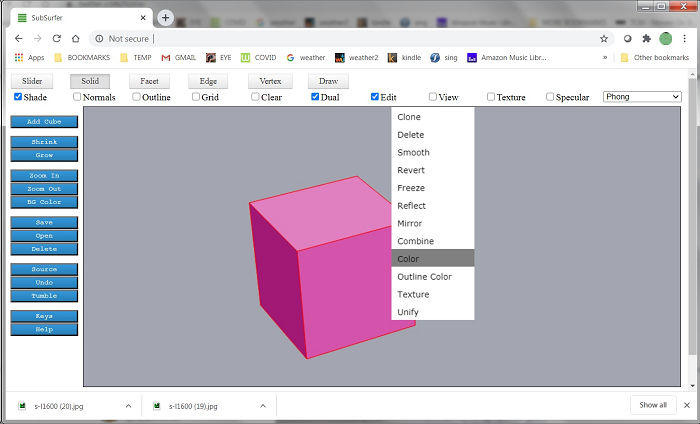
Modeling in Subsurfer is based on cubes, and every model starts as a cube. The buttons at the top select the current tool. Using the Solid tool, you can right-click on a solid and change some of its attributes, such as color. Panning, zooming and rotation of the model are done using the Slider tool. The context menus and color picker are implemented within the Canvas control. This 3D projection and all model editing are done in the 2D context.

Models are developed by applying successive subdivision surfaces to solids, combined with extrusion and splitting of facets. The interface is a combination of keystroke commands plus right-click menus using the Solid, Facet, Edge and Vertex tools. Here, we see successive applications of surface subdivision on a cube.

The check boxes control viewing options. Here, we see the same model with Clear and Outline options checked.

Here, we see a facet that has been extruded. Extrusion is a right-click menu item and a keystroke command. Facets are selected using the Facet tool. You can click a facet, click and roll to select several facets, or drag a box to net-select facets.
One important thing when extruding facets is to avoid having common internal walls. This can happen when extruding multiple adjacent facets whose normals are pointing in the same direction. Shared internal walls will confuse the Catmull-Clark algorithm and the results don't look right. To avoid this, when extruding adjacent facets, unless their normals are facing in different directions, it's better to use the Extrude Group command.

Edge loops affect how surface subdivision will shape a model. Edge loops can be added by using the Bevel command (Facet tool), or using the Split command (Edge tool). Edge loops can be selected with a right-click menu option of the Edge tool.
Every facet in Subsurfer is a quadrilateral. Quadrilaterals are handled well by the Catmull-Clark algorithm, and they make it easier to implement algorithms which can traverse the model to find edge loops and facet loops.

The vertex tool can be used to drag vertices, just as the Facet tool can drag facets and the Edge tool can drag edges. When dragging model elements, it is important to have the grid displayed (Grid check box option) so you will be aware of which 2 dimensions you are dragging in. Otherwise, the results may be unexpected and unwelcome.

Subsurfer has an Edit window (2D canvas context) and a View window (3D canvas context). They are controlled by the Edit and View check boxes. Here, we see a model in the Edit window alongside its WebGL equivalent in the View window.

Subdivision surface modeling produces shapes with smoothly rounded curves. With careful planning and patient editing, complex models can be produced by extrusion, splitting, scaling and tilting of facets, translation of edges and vertices, and successive applications of the smoothing algorithm.

Here is the mesh view of the spacepig model in the Edit window. Like all Subsurfer models, it started as a cube.

Subsurfer supports a handful of built-in textures, such as wood grain (shown below). An image file called textures.png contains all the textures.
If you want to run the program from your file system, browser security settings will not allow the web page to load the texture image. Both the HTML page and the PNG image have to be hosted on the same server. You can run the program from localhost if you have the proper software to set that up. Or you can run Chrome.exe with a special command line option to allow loading of the textures from the file system. The command you need to execute is "chrome.exe --allow-file-access-from-files". You will have to close all instances of Chrome before doing this.

A variety of textures are included, including the mod paisley seen below. There is an Extrude Series command that automates successive extrusion of facets, which lends itself to the creation of hallucinatory, Lovecraftian nightmares.



The Source command (left side buttons) opens a new tab that displays a text representation of the current model mesh.

The Save, Open and Delete buttons were implemented and tested using AJAX calls to store the models on a server and retrieve them by name. But since I don't want any hits on my server for the purposes of this article, I have changed the paths and names so the buttons don't do anything. You could still use the AJAX code provided, but you would have to implement your own SOAP web services and change the client side code to match.
However, you can still save your models in a local file by copying the text from the Source command as shown above. If you want to enter a model you've saved locally into Subsurfer, use the Input button. It's one of the commands on the left hand side, but it's not shown on these pictures. The Input command brings up a form and you just paste the mesh text into the field as shown below. This seems to work quite well even for large models. You may run into issues with browser security settings, but it worked fine for me.

A variety of WebGL shaders are included which can be chosen from the dropdown menu at the top right. Shaders in WebGL are implemented using GLSL. Flat shading and Phong (smooth) shading with optional specularity are the most useful. Flat shading should be used for sharp-edged objects. Cubes look funny with Phong shading. I have also implemented a few non-realistic custom shaders, including the festive rainbow shader pictured below (this is not a texture, it's a custom shader). This shader is sensitive to the object's location in space, so the colors will change in a very trippy way as the object rotates.

There is a help file and a list of keystrokes built into the program (last two buttons on left side), but the quickest way to get started playing with Subsurfer is to experiment by extruding facets and smoothing solids using keystroke commands, just to see what kinds of weird and interesting models you can make. The keystroke command to extrude a facet is 'e' and the keystroke command to smooth a solid is 's'. You will want to have the Facet tool chosen so you can select facets. You can rotate the model using the Facet tool (and most of the other tools) by doing right-click + dragging in the window. Plus and minus keys will zoom in or out. Click on a facet to select it. You can also net select facets and click+drag to select areas. It's possible to extrude multiple facets at the same time. But if doing multiple extrudes, make sure the facets are not facing in the exact same direction or you will end up with shared internal walls that throw off the subdivision algorithm. If extruding neighboring facets that face the same direction, better to use Extrude Group (keystroke 'g') instead.
Using the Code
You can just run the HTML file from your local file system. As mentioned above, if running locally, you will run into security issues and textures will not display in WebGL.
To get around this problem, close all instances of Chrome and start Chrome with this command: "chrome.exe --allow-file-access-from-files".
Also, the Save, Open and Delete buttons are effectively disabled. To save a model, copy the mesh specification using the Source command (left-hand buttons). To enter the saved model into Subsurfer, use the Input command and paste the mesh text into the form provided.
One important thing when extruding facets is to avoid having common internal walls. This can happen when extruding multiple adjacent facets whose normals are pointing in the same direction. Internal walls will mess up the results of the Catmull-Clark algorithm. To avoid this, when extruding adjacent facets, unless their normals are facing in different directions, it's better to use the Extrude Group command.
Building the Edit View
There are about 14000 lines of code in the application. The WebGL part makes use of the Sylvester matrix math library of James Coglan, which is used per the license agreement. In this article I will touch on a few of the basic elements that make the program work. I may cover some topics more in depth in future articles.
This section is about how the 3D projection for the edit view is produced in a 2D drawing context.
The program makes use of the HTML5 Canvas control, which has two contexts. Here is the function which initializes the program UI. It adds two Canvas controls and obtains the 2D context for one and the webgl (3D) context for the other one. If webgl is not available, it falls back to experimental-webgl. The WebGL features seem well supported on all major browsers. The rest of the code sets up listeners for user input and attends to other housekeeping such as adding the available shader options to a listbox.
function startModel()
{
alertUser("");
filename = "";
setInterval(timerEvent, 10);
makeCube();
canvas = document.createElement('canvas');
canvas2 = document.createElement('canvas');
document.body.appendChild(canvas);
document.body.appendChild(canvas2);
canvas.style.position = 'fixed';
canvas2.style.position = 'fixed';
ctx = canvas.getContext('2d');
gl = canvas2.getContext("webgl") || canvas2.getContext("experimental-webgl");
pos = new Point(0, 0);
lastClickPos = new Point(0, 0);
window.addEventListener('resize', resize);
window.addEventListener('keydown', keyDown);
window.addEventListener('keyup', keyRelease);
canvas.addEventListener('mousemove', mouseMove);
canvas.addEventListener('mousedown', mouseDown);
canvas.addEventListener('mouseup', mouseUp);
canvas.addEventListener('mouseenter', setPosition);
canvas.addEventListener('click', click);
canvas2.addEventListener('mousemove', mouseMoveGL);
canvas2.addEventListener('mousedown', mouseDownGL);
canvas2.addEventListener('mouseup', mouseUpGL);
canvas.style.backgroundColor = colorString(canvasBackgroundColor, false);
canvas.style.position = "absolute";
canvas.style.border = '1px solid black';
canvas2.style.position = "absolute";
canvas2.style.border = '1px solid black';
resize();
document.getElementById("checkboxoutlines").checked = false;
document.getElementById("checkboxsolid").checked = true;
document.getElementById("checkboxgrid").checked = false;
document.getElementById("toolslider").checked = true;
document.getElementById("checkboxtwosided").checked = true;
document.getElementById("checkboxwebgl").checked = false;
document.getElementById("checkbox2DWindow").checked = true;
document.getElementById("checkboxtransparent").checked = false;
if (gl != null)
{
gl.clearColor(canvasBackgroundColor.R / 255.0,
canvasBackgroundColor.G / 255.0, canvasBackgroundColor.B / 255.0, 1.0);
gl.enable(gl.DEPTH_TEST);
gl.depthFunc(gl.LEQUAL);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
}
addShaderToList("Phong");
addShaderToList("Rainbow 1");
addShaderToList("Rainbow 2");
addShaderToList("Stripes");
addShaderToList("Chrome");
addShaderToList("Smear");
addShaderToList("Flat");
addShaderToList("T-Map");
addShaderToList("Comic");
addShaderToList("Comic 2");
addShaderToList("Topo");
addShaderToList("Paint By Numbers");
var rect = canvas.getBoundingClientRect();
origin = new Point(-(rect.width / 2), -(rect.height / 2));
setEditViewOptions();
hideInputForm();
}
For various reasons, all the editing in the program is done in a 2D context because it seemed easier for me to solve problems related to hit detection and user interaction in the 2D context. Drawing in the 2D context is also a lot simpler than drawing in WebGL.
There are only a few things that need to happen in order to create a 3D projection in 2D. Here is the projection code that maps a 3D point into two dimensions. To accomplish this, it is only necessary to imagine an X/Y plane situated along the Z axis between the model and the eye of the viewer. Then calculate where a ray drawn from the eye to each 3D model vertex would intersect that plane.
function To2D(p3d)
{
var point3d = new Point3D(p3d.x, p3d.y, p3d.z);
RotateXYZ(point3d, myCenter, radiansX, radiansY, radiansZ);
var xRise = point3d.x - myCenter.x;
var yRise = point3d.y - myCenter.y;
var zRunEye = zEyePlane - point3d.z;
var zRunView = zViewingPlane - point3d.z;
var factor = (zRunEye - zRunView) / zRunEye;
var x = (myCenter.x + (factor * xRise));
var y = (myCenter.y + (factor * yRise));
x *= ctx.canvas.width;
x /= docSize;
y *= ctx.canvas.width;
y /= docSize;
var p = new Point(Math.floor(x), -Math.floor(y));
p.x -= origin.x;
p.y -= origin.y;
return p;
}
Note that the first thing the above function does is to rotate the point from its actual position to the current viewing position. This is to provide a way for the user to rotate the work and view it from all sides. This too is a trivial matter as seen below. Whenever the user enters mouse input to rotate the view, the variables radiansX, radiansY and radiansZ are updated and the projection is redrawn.
function RotateXYZ(p, rotation_point, radiansX, radiansY, radiansZ)
{
if (radiansZ != 0.0)
{
radiansZ = normalize_radians(radiansZ);
if (radiansZ != 0)
{
var ydiff = (p.y) - (rotation_point.y);
var xdiff = (p.x) - (rotation_point.x);
var xd = (xdiff * Math.cos(radiansZ)) - (ydiff * Math.sin(radiansZ));
xd = Math.round(xd, 0);
var yd = (xdiff * Math.sin(radiansZ)) + (ydiff * Math.cos(radiansZ));
yd = Math.round(yd, 0);
p.x = rotation_point.x + (xd);
p.y = rotation_point.y + (yd);
}
}
if (radiansY != 0.0)
{
radiansY = normalize_radians(radiansY);
if (radiansY != 0)
{
var zdiff = (p.z) - (rotation_point.z);
var xdiff = (p.x) - (rotation_point.x);
var xd = (xdiff * Math.cos(radiansY)) - (zdiff * Math.sin(radiansY));
xd = Math.round(xd, 0);
var zd = (xdiff * Math.sin(radiansY)) + (zdiff * Math.cos(radiansY));
zd = Math.round(zd, 0);
p.x = rotation_point.x + (xd);
p.z = rotation_point.z + (zd);
}
}
if (radiansX != 0.0)
{
radiansX = normalize_radians(radiansX);
if (radiansX != 0)
{
var ydiff = (p.y) - (rotation_point.y);
var zdiff = (p.z) - (rotation_point.z);
var zd = (zdiff * Math.cos(radiansX)) - (ydiff * Math.sin(radiansX));
zd = Math.round(zd, 0);
var yd = (zdiff * Math.sin(radiansX)) + (ydiff * Math.cos(radiansX));
yd = Math.round(yd, 0);
p.z = rotation_point.z + (zd);
p.y = rotation_point.y + (yd);
}
}
}
A model consists of facets. Facets consist of edges, and edges consist of points. Here are the basic data structures that hold a model. Please note that for the purposes of this program, a cube is still a cube no matter how many facets it has. Every model starts as a cube with 6 facets, but more facets will be added to the cube as extrusions, splits, and smoothing algorithms are applied.
function cube(left, right, top, bottom, front, back)
{
if (left == undefined)
{
left = 0;
}
if (right == undefined)
{
right = 0;
}
if (top == undefined)
{
top = 0;
}
if (bottom == undefined)
{
bottom = 0;
}
if (front == undefined)
{
front = 0;
}
if (back == undefined)
{
back = 0;
}
this.color = new Color(190, 180, 190);
this.outlineColor = new Color(0, 0, 0);
this.textureName = "";
this.nSubdivide = 0;
this.left = left;
this.right = right;
this.top = top;
this.bottom = bottom;
this.front = front;
this.back = back;
this.previousFacetLists = [];
this.facets = [];
var lefttopback = new Point3D(left, top, back);
var lefttopfront = new Point3D(left, top, front);
var righttopfront = new Point3D(right, top, front);
var righttopback = new Point3D(right, top, back);
var leftbottomback = new Point3D(left, bottom, back);
var leftbottomfront = new Point3D(left, bottom, front);
var rightbottomfront = new Point3D(right, bottom, front);
var rightbottomback = new Point3D(right, bottom, back);
var topPoints = [];
topPoints.push(clonePoint3D(lefttopback));
topPoints.push(clonePoint3D(righttopback));
topPoints.push(clonePoint3D(righttopfront));
topPoints.push(clonePoint3D(lefttopfront));
topPoints.reverse();
var bottomPoints = [];
bottomPoints.push(clonePoint3D(leftbottomfront));
bottomPoints.push(clonePoint3D(rightbottomfront));
bottomPoints.push(clonePoint3D(rightbottomback));
bottomPoints.push(clonePoint3D(leftbottomback));
bottomPoints.reverse();
var frontPoints = [];
frontPoints.push(clonePoint3D(lefttopfront));
frontPoints.push(clonePoint3D(righttopfront));
frontPoints.push(clonePoint3D(rightbottomfront));
frontPoints.push(clonePoint3D(leftbottomfront));
frontPoints.reverse();
var backPoints = [];
backPoints.push(clonePoint3D(righttopback));
backPoints.push(clonePoint3D(lefttopback));
backPoints.push(clonePoint3D(leftbottomback));
backPoints.push(clonePoint3D(rightbottomback));
backPoints.reverse();
var leftPoints = [];
leftPoints.push(clonePoint3D(lefttopback));
leftPoints.push(clonePoint3D(lefttopfront));
leftPoints.push(clonePoint3D(leftbottomfront));
leftPoints.push(clonePoint3D(leftbottomback));
leftPoints.reverse();
var rightPoints = [];
rightPoints.push(clonePoint3D(righttopfront));
rightPoints.push(clonePoint3D(righttopback));
rightPoints.push(clonePoint3D(rightbottomback));
rightPoints.push(clonePoint3D(rightbottomfront));
rightPoints.reverse();
var id = 1;
var s1 = new Facet();
s1.ID = id++;
s1.points = topPoints;
this.facets.push(s1);
var s2 = new Facet();
s2.ID = id++;
s2.points = bottomPoints;
this.facets.push(s2);
var s3 = new Facet();
s3.ID = id++;
s3.points = backPoints;
this.facets.push(s3);
var s4 = new Facet();
s4.ID = id++;
s4.points = frontPoints;
this.facets.push(s4);
var s5 = new Facet();
s5.ID = id++;
s5.points = leftPoints;
this.facets.push(s5);
var s6 = new Facet();
s6.ID = id++;
s6.points = rightPoints;
this.facets.push(s6);
for (var n = 0; n < this.facets.length; n++)
{
this.facets[n].cube = this;
}
}
function Facet()
{
this.cube = -1;
this.ID = -1;
this.points = [];
this.point1 = new Point(0, 0);
this.point2 = new Point(0, 0);
this.closed = false;
this.fill = false;
this.averagePoint3D = new Point3D(0, 0, 0);
this.normal = -1;
this.edges = [];
this.neighbors = [];
this.greatestRotatedZ = 0;
this.greatestLeastRotatedZ = 0;
this.averageRotatedZ = 0;
this.boundsMin = new Point3D(0, 0, 0);
this.boundsMax = new Point3D(0, 0, 0);
}
function Point3D(x, y, z)
{
this.x = x;
this.y = y;
this.z = z;
}
To draw the model in 2D, it is only necessary to map the polygons described by each facet from 3D to 2D, then fill the resulting 2D polygons. There are only two complications. The first is that each facet must be shaded according to its angle relative to a vector which represents a light source. The second is that the facets must be sorted from back to front according to their position along the Z axis, given the current view rotation. This way, the facets on the back get drawn first, and the ones on the front obscure them, which is what you want.
It should be noted that this method of portraying a solid object by sorting polygons along the Z axis is an approximation. It does not take into account intersections between facets. Also, when objects contain concavities, the Z sort can give results which look incorrect. However the method produces good enough results when the object has no concavities and no intersections between surfaces. The occurence of anomolies is greatly reduced when the facets are small relative to the size of the model, as when smoothing has been applied. Where irregularities exist, you can always work around them during editing by rotating the model and/or using the Clear and Outline viewing options and treating the model as a wireframe with transparent surfaces. Any aberrations of this kind will not appear in the View window, since WebGL handles all these cases correctly.
To shade a polygon, it is necessary to obtain its normal. This is a vector perpendicular to the facet surface (calculated using a cross product). The angle between this normal and the light source vector is calculated (using a dot product), and this is used to brighten or darken the facet color. If the angle is closer to 0, the facet color is lightened. If the angle is closer to 180, the facet color is darkened. Here is the code which calculates the facet normal and shades the facet.
function CalculateNormal(facet)
{
var normal = -1;
if (facet.points.length > 2)
{
var p0 = facet.points[0];
var p1 = facet.points[1];
var p2 = facet.points[2];
var a = timesPoint(minusPoints(p1, p0), 8);
var b = timesPoint(minusPoints(p2, p0), 8);
normal = new line(clonePoint3D(p0),
new Point3D((a.y * b.z) - (a.z * b.y),
-((a.x * b.z) - (a.z * b.x)),
(a.x * b.y) - (a.y * b.x))
);
normal.end = LengthPoint(normal, cubeSize * 2);
var avg = averageFacetPoint(facet.points);
normal.end.x += avg.x - normal.start.x;
normal.end.y += avg.y - normal.start.y;
normal.end.z += avg.z - normal.start.z;
normal.start = avg;
}
return normal;
}
function getLightSourceAngle(normal)
{
var angle = 0;
if (normal != -1)
{
angle = normalize_radians(vectorAngle
(lightSource, minusPoints(ToRotated(normal.end), ToRotated(normal.start))));
}
return angle;
}
function vectorAngle(vector1, vector2)
{
var angle = 0.0;
var length1 = Math.sqrt((vector1.x * vector1.x) + (vector1.y * vector1.y) +
(vector1.z * vector1.z));
var length2 = Math.sqrt((vector2.x * vector2.x) + (vector2.y * vector2.y) +
(vector2.z * vector2.z));
var dot_product = (vector1.x * vector2.x + vector1.y * vector2.y + vector1.z * vector2.z);
var cosine_of_angle = dot_product / (length1 * length2);
angle = Math.acos(cosine_of_angle);
return angle;
}
function ShadeFacet(color, angle)
{
var darken_range = 0.75;
var lighten_range = 0.75;
var result = new Color(color.R, color.G, color.B);
if (angle > 180)
{
angle = 360 - angle;
}
if (angle > 90)
{
var darken_amount = (angle - 90) / 90;
darken_amount *= darken_range;
var r = color.R - (color.R * darken_amount);
var g = color.G - (color.G * darken_amount);
var b = color.B - (color.B * darken_amount);
r = Math.min(255, Math.max(0, r));
g = Math.min(255, Math.max(0, g));
b = Math.min(255, Math.max(0, b));
result = new Color(r, g, b);
}
else
{
var lighten_amount = (90 - angle) / 90;
lighten_amount *= lighten_range;
var r = color.R + ((255 - color.R) * lighten_amount);
var g = color.G + ((255 - color.G) * lighten_amount);
var b = color.B + ((255 - color.B) * lighten_amount);
r = Math.max(0, Math.min(255, r));
g = Math.max(0, Math.min(255, g));
b = Math.max(0, Math.min(255, b));
result = new Color(r, g, b);
}
return result;
}
Once the facets are shaded, it is necessary to sort them back to front, so that when you draw them in order the nearest ones will cover up the ones that are behind them.
function sortFacets()
{
allFacets = [];
for (var w = 0; w < cubes.length; w++)
{
var cube = cubes[w];
for (var i = 0; i < cube.facets.length; i++)
{
allFacets.push(cube.facets[i]);
}
}
sortFacetsOnZ(allFacets);
}
function sortFacetsOnZ(facets)
{
for (var i = 0; i < facets.length; i++)
{
setAverageAndGreatestRotatedZ(facets[i]);
}
facets.sort(
function(a, b)
{
if (a.greatestRotatedZ == b.greatestRotatedZ)
{
if (a.leastRotatedZ == b.leastRotatedZ)
{
return a.averageRotatedZ - b.averageRotatedZ;
}
else
{
return a.leastRotatedZ - b.leastRotatedZ;
}
}
else
{
return a.greatestRotatedZ - b.greatestRotatedZ
}
}
);
}
Here then is some of the code that draws the editing display with a 3D projection in a 2D context. The fundamental things going on here are sortFacets() and drawCubes(). This is what produces the 3D projection that gives the illusion of a solid shape. The other code here has to do with updating the WebGL view and drawing elements of the editing UI. The editing UI elements consist of the rectangular orientation grid and context menus, plus model elements (facets, edges, vertices) which are subject to rollover behavior and highlight behavior and must be redrawn in different colors according to the current tool and the position of the mouse.
function updateModel()
{
for (var c = 0; c < cubes.length; c++)
{
updateCube(cubes[c]);
}
sortFacets();
reloadSceneGL();
draw();
}
function draw()
{
if (isGL && gl != null)
{
drawSceneGL();
}
if (is2dWindow || !isGL)
{
ctx.clearRect(0, 0, canvas.width, canvas.height);
findGridOrientation();
if (gridChosen())
{
drawGridXY();
}
lineColor = lineColorShape;
drawCubes();
if (mouseIsDown && draggingShape)
{
draw3DRectangleFrom2DPoints(mouseDownPos, pos, false, "white");
}
if (hitLine != -1)
{
var pts = [];
pts.push(To2D(hitLine.start));
pts.push(To2D(hitLine.end));
drawPolygonHighlighted(pts);
}
if (hitFacet != -1 && toolChosen() == "facet")
{
drawPolygon3d(hitFacet.points, true, true, "yellow", true);
}
for (var g = 0; g < selectedLines.length; g++)
{
var pts = [];
pts.push(To2D(selectedLines[g].start));
pts.push(To2D(selectedLines[g].end));
drawPolygonSelected(pts);
}
if (hitVertex != -1)
{
drawVertex(hitVertex, false);
}
for (var qq = 0; qq < selectedVertexes.length; qq++)
{
drawVertex(selectedVertexes[qq], true);
}
if (lineDiv != -1 &&
lineDiv2 != -1)
{
drawLine2D(lineDiv, "blue");
drawLine2D(lineDiv2, "blue");
}
if (draggingRect)
{
draw2DRectangleFrom2DPoints(mouseDownPos, pos, "black");
}
if (colorPickMode.length > 0)
{
drawColors(0, 0, colorPickHeight);
}
drawMenu();
}
}
function drawCubes()
{
var drawlines = isOutline || !isShade;
var drawNormals = isNormals;
var shadeSolids = isShade;
var dual = isDualSided;
for (var i = 0; i < allFacets.length; i++)
{
var facet = allFacets[i];
if (facet.normal == -1)
{
facet.normal = CalculateNormal(facet);
}
var c = facet.cube.color;
if (colorPickMode.length == 0)
{
if (facet.cube == hitSolid)
{
c = new Color(23, 100, 123);
}
if (listHas(selectedSolids, facet.cube))
{
c = new Color(200, 30, 144);
}
if (listHas(selectedFacets, facet))
{
c = new Color(0, 255, 255);
}
}
c = ShadeFacet(c, degrees_from_radians(getLightSourceAngle(facet.normal)));
var show = true;
if (!dual)
{
show = ShowFacet(degrees_from_radians(getFrontSourceAngle(facet.normal)));
}
var colorFillStyle = colorString(c, isTransparent);
var colorOutlineStyle = colorString(facet.cube.outlineColor, isTransparent);
if (listHas(selectedSolids, facet.cube))
{
drawlines = true;
colorOutlineStyle = "red";
}
if (show)
{
drawPolygon3d(facet.points, true, shadeSolids || listHas(selectedFacets, facet),
colorFillStyle, drawlines, colorOutlineStyle);
if (drawNormals)
{
drawLine3D(facet.normal, "magenta");
}
}
}
}
function drawPolygon3d(points, isClosed, isFill, fillColor, isOutline, outlineColor)
{
var result = [];
if (points.length > 0)
{
for (var i = 0; i < points.length; i++)
{
result.push(To2D(points[i]));
}
drawPolygon(result, isClosed, isFill, fillColor, isOutline, outlineColor);
}
}
function drawPolygon
(points, isClosed, isFill, fillColor, isOutline, outlineColor, lineThickness)
{
if (points.length > 0)
{
isClosed = isClosed ? isClosed : false;
isFill = isFill ? isFill : false;
if (isOutline === undefined)
{
isOutline = true;
}
if (lineThickness === undefined)
{
lineThickness = 1;
}
if (outlineColor === undefined)
{
outlineColor = lineColor;
}
ctx.beginPath();
ctx.lineWidth = lineThickness;
ctx.lineCap = 'round';
ctx.strokeStyle = outlineColor;
if (isFill)
{
ctx.fillStyle = fillColor;
}
ctx.moveTo(points[0].x, points[0].y);
for (var i = 1; i < points.length; i++)
{
ctx.lineTo(points[i].x, points[i].y);
}
if (isClosed)
{
ctx.lineTo(points[0].x, points[0].y);
}
if (isFill)
{
ctx.fill();
}
if (isOutline)
{
ctx.stroke();
}
}
}
Building the WebGL Model
So the production of the 2D editing view is fairly straightforward. The production of the WebGL view is a little harder and will be discussed more in depth in a future article. I will only show some of the code which binds our JavaScript data structures to the WebGL representation of our model. There are five basic elements which must be buffered and bound to WebGL. Here is the main function that does that work.
function bindModelGL()
{
bindVerticesGL();
bindColorsGL();
bindVertexIndicesGL();
bindTextureCoordinatesGL();
bindNormalsGL();
}
Binding the colors to our model. Each cube can only be a single color. Every facet has a pointer back to its parent cube. Please note that for our purposes a cube is just a list of facets, which may or may not be an actual cube. The list of all facets will give us the correct color for every vertex. We need 4 elements for every vertex: R, G, B, and A (alpha channel which indicates transparency). We use 1.0 for A, so our WebGL models will always be opaque.
function bindColorsGL()
{
if (isGL && gl != null)
{
var generatedColors = [];
for (var i = 0; i < allFacets.length; i++)
{
var f = allFacets[i];
var c = color2FromColor(f.cube.color);
var b = [];
b.push(c.R);
b.push(c.G);
b.push(c.B);
b.push(1.0);
for (var s = 0; s < 4; s++)
{
generatedColors.push(b[0]);
generatedColors.push(b[1]);
generatedColors.push(b[2]);
generatedColors.push(b[3]);
}
}
cubeVerticesColorBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, cubeVerticesColorBuffer);
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(generatedColors), gl.STATIC_DRAW);
}
}
We have to bind the facet normals so WebGL can shade the model. Note that for each facet normal, we only need 3 numbers. This is because WebGL only cares about the direction of the normal, not its location in space.
A specific wrinkle here is that Subsurfer supports Phong shading, which needs vertex normals. If you think of each facet normal as being perpendicular to the facet surface, then the vertex normal is the average of the normals of all the facets which contain that vertex. So when Phong shading is in effect, the vertex normals must be calculated. We don't use these in the 2D projection because we only do flat shading, so we just need the facet normals. But vertex normals are needed for Phong shading in WebGL. If we are doing flat shading in WebGL, then we don't have to calculate the vertex normals. In the case of flat shading, we just use the facet normal as the normal for each vertex.
function bindNormalsGL()
{
if (isGL && gl != null)
{
cubeVerticesNormalBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, cubeVerticesNormalBuffer);
var vertexNormals = [];
for (q = 0; q < allFacets.length; q++)
{
var f = allFacets[q];
if (f.normal == -1)
{
f.normal = CalculateNormal(f);
}
}
if (fastVertexNormalMethod)
{
if (isSmoothShading())
{
allSortedPoints = getFacetPointsAndSetUpBackPointers(allFacets);
sortPointsByXYZ(allSortedPoints);
stageVertexNeighborFacets(allSortedPoints);
}
}
if (isSmoothShading())
{
for (q = 0; q < allFacets.length; q++)
{
var f = allFacets[q];
for (var j = 0; j < f.points.length; j++)
{
var p = f.points[j];
var vn = p.vertexNormal;
if (vn == undefined)
{
vn = calculateVertexNormal(p, allFacets);
p.vertexNormal = vn;
}
vertexNormals.push((vn.end.x / reductionFactor) -
(vn.start.x / reductionFactor));
vertexNormals.push((vn.end.y / reductionFactor) -
(vn.start.y / reductionFactor));
vertexNormals.push((vn.end.z / reductionFactor) -
(vn.start.z / reductionFactor));
}
}
}
else
{
for (q = 0; q < allFacets.length; q++)
{
var f = allFacets[q];
for (var i = 0; i < 4; i++)
{
vertexNormals.push((f.normal.end.x / reductionFactor) -
(f.normal.start.x / reductionFactor));
vertexNormals.push((f.normal.end.y / reductionFactor) -
(f.normal.start.y / reductionFactor));
vertexNormals.push((f.normal.end.z / reductionFactor) -
(f.normal.start.z / reductionFactor));
}
}
}
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertexNormals), gl.STATIC_DRAW);
}
}
We must bind each vertex in the model. Even though WebGL needs triangles instead of quadrilaterals to work properly, the vertices don't have to be duplicated because we will supply a list of indices into the vertex buffer. Some of the indices will be repeated, which gives us our triangles.
function bindVerticesGL()
{
cubeVerticesBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, cubeVerticesBuffer);
var vertices = [];
for (var i = 0; i < allFacets.length; i++)
{
var f = allFacets[i];
for (var j = 0; j < f.points.length; j++)
{
var point3d = f.points[j];
vertices.push(point3d.x / reductionFactor);
vertices.push(point3d.y / reductionFactor);
vertices.push((point3d.z / reductionFactor));
}
}
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);
}
Here, we build the vertex indices buffer and bind it to WebGL. The index pattern 0, 1, 2 followed by 0, 2, 3 is what divides our four facet vertices into two triangles.
function bindVertexIndicesGL()
{
cubeVerticesIndexBuffer = gl.createBuffer();
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, cubeVerticesIndexBuffer);
var cubeVertexIndices = [];
var t = 0;
for (var i = 0; i < allFacets.length; i++)
{
cubeVertexIndices.push(t + 0);
cubeVertexIndices.push(t + 1);
cubeVertexIndices.push(t + 2);
cubeVertexIndices.push(t + 0);
cubeVertexIndices.push(t + 2);
cubeVertexIndices.push(t + 3);
t += 4;
}
gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, new Uint16Array(cubeVertexIndices), gl.STATIC_DRAW);
}
Each vertex in our model has X, Y, Z for position in space, plus two other coordinates U and V which are offsets into a texture image. The U and V values range between 0 and 1. For complex shapes, we assign U and V coordinates automatically as if the texture were wrapped around the image. This is done by the function assignPolarUV_2().
function bindTextureCoordinatesGL()
{
for (var i = 0; i < cubes.length; i++)
{
assignPolarUV_2(cubes[i], i);
}
cubeVerticesTextureCoordBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, cubeVerticesTextureCoordBuffer);
var textureCoordinates = [];
for (var i = 0; i < allFacets.length; i++)
{
if (isPolarUV)
{
var f = allFacets[i];
textureCoordinates.push(f.points[0].u);
textureCoordinates.push(f.points[0].v);
textureCoordinates.push(f.points[1].u);
textureCoordinates.push(f.points[1].v);
textureCoordinates.push(f.points[2].u);
textureCoordinates.push(f.points[2].v);
textureCoordinates.push(f.points[3].u);
textureCoordinates.push(f.points[3].v);
}
else
{
textureCoordinates.push(0.0);
textureCoordinates.push(0.0);
textureCoordinates.push(1.0);
textureCoordinates.push(0.0);
textureCoordinates.push(1.0);
textureCoordinates.push(1.0);
textureCoordinates.push(0.0);
textureCoordinates.push(1.0);
}
}
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(textureCoordinates),
gl.STATIC_DRAW);
}
Flat Shaders
When addressing WebGL directly, it is necessary to write your own shaders. These are written in a language called GLSL. Each shader must have a main() procedure. A shader is a little program that is compiled and loaded on your computer's graphics chip.
Shaders are contained in script tags in your HTML file and can be addressed by name. You need different shaders if you are using a texture for your model as opposed to just a solid color. Subsurfer has flat shaders for both color and texture, and Phong (smooth) shaders for both color and texture. There are several wacky custom shaders included as well. Here, I will just mention the flat shaders and Phong shaders for the case of a solid color.
Here are the flat shaders for a solid color. You must provide a vertex shader and a fragment shader. This is true for every type of shading you implement. The vertex shader gives you the color for each vertex. The fragment shader can interpolate between vertices to create a smoother appearance. It basically shades each individual pixel.
The flat shader below gives an appearance very similar to the 3D projection we built in JavaScript which displays in the edit window. If you look at what this vertex shader is doing, it's actually the same calculations as we saw previously in JavaScript in the function shadeFacet(). It's taking the angle (dot product) between the vertex normal (in this case, the same as the facet normal) and the light source directional vector, and using that to lighten or darken the facet color. But the shader can do it much faster because it's running on a massively parallel device. Also, it takes into account the color of the light, as well as factoring in both a directional light and an ambient light. Note that in this shader, the light colors and direction are hard coded in.
The fragment shader here doesn't do much, it's just a pass-through. That's because there is no interpolation or smoothing for a flat shader, so all the pixels on the facet can be shaded the same color.
<script id="vertex-shader-color-flat" type="x-shader/x-vertex">
// VERTEX SHADER COLOR (FLAT)
attribute highp vec3 aVertexNormal;
attribute highp vec3 aVertexPosition;
attribute vec4 aVertexColor;
uniform highp mat4 uNormalMatrix;
uniform highp mat4 uMVMatrix;
uniform highp mat4 uPMatrix;
varying highp vec3 vLighting;
varying lowp vec4 vColor;
void main(void) {
gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition, 1.0);
highp vec3 ambientLight = vec3(0.5, 0.5, 0.5);
highp vec3 directionalLightColor = vec3(0.5, 0.5, 0.5);
highp vec3 directionalVector = vec3(0.85, 0.8, 0.75);
highp vec4 transformedNormal = uNormalMatrix * vec4(aVertexNormal, 1.0);
highp float directional = max(dot(transformedNormal.xyz, directionalVector), 0.0);
vLighting = ambientLight + (directionalLightColor * directional);
vColor = aVertexColor;
}
</script>
<script id="fragment-shader-color-flat" type="x-shader/x-fragment">
// FRAGMENT SHADER COLOR (FLAT)
varying lowp vec4 vColor;
varying highp vec3 vLighting;
uniform sampler2D uSampler;
void main(void) {
gl_FragColor = vec4(vColor.rgb * vLighting, 1.0);
}
</script>
Phong Shaders
Phong shading gives a smoother appearance because it interpolates between vertices to individually shade each pixel. The color Phong shaders are shown below.
Notice that not much is going on here with the vertex shader. Most of the action is happening in the fragment shader, because we are going to calculate each individual pixel. The most interesting thing to note about the vertex shader is that the transformed vertex normal is declared as "varying". This will cause it to be smoothly interpolated for each pixel in the fragment shader.
So this fragment shader is actually using a different normal for each pixel. You don't see any explicit code to do that because it's built into the GLSL language and the "varying" type. As in the flat shader, the colors of the ambient and directional lights are hard coded in, and so is the direction of the light. Also, the calculation of the color by using the angle between the light direction vector and the vertex normal is very similar to the flat shaders. The difference here is that calculation is happening in the fragment shader, using a different interpolated normal value for each pixel. That's what gives the smooth appearance. The Phong shader is a slower shader than the flat shader, because it has to do far more calculations.
One last thing to note about the Phong shader is that I have implemented specularity. If the "Specular" check box on the UI is checked, the uniform value specularUniform will be set to 1. If this happens, wherever the angle between the light source and the vertex normal is sufficiently small, the color of that pixel will be automatically set to white. This produces specular highlights that make the model look shiny.
<script id="shader-vs-normals-notexture-phong" type="x-shader/x-vertex">
attribute highp vec3 aVertexNormal;
attribute highp vec3 aVertexPosition;
attribute vec4 aVertexColor;
uniform highp mat4 uNormalMatrix;
uniform highp mat4 uMVMatrix;
uniform highp mat4 uPMatrix;
varying vec3 vTransformedNormal;
varying vec4 vPosition;
varying lowp vec4 vColor;
void main(void)
{
vPosition = uMVMatrix * vec4(aVertexPosition, 1.0);
gl_Position = uPMatrix * vPosition;
vTransformedNormal = vec3(uNormalMatrix * vec4(aVertexNormal, 1.0));
vColor = aVertexColor;
}
</script>
<script id="shader-fs-normals-notexture-phong" type="x-shader/x-fragment">
precision mediump float;
uniform int specularUniform;
varying vec3 vTransformedNormal;
varying vec4 vPosition;
varying lowp vec4 vColor;
void main(void) {
vec3 pointLightingLocation;
pointLightingLocation = vec3(0, 13.5, 13.5);
vec3 ambientColor;
ambientColor = vec3(0.5, 0.5, 0.5);
vec3 pointLightingColor;
pointLightingColor = vec3(0.5, 0.5, 0.5);
vec3 lightWeighting;
vec3 lightDirection = normalize(pointLightingLocation - vPosition.xyz);
float directionalLightWeighting = max(dot(normalize(vTransformedNormal),
lightDirection), 0.0);
lightWeighting = ambientColor + pointLightingColor * directionalLightWeighting;
vec4 fragmentColor;
fragmentColor = vColor;
gl_FragColor = vec4(fragmentColor.rgb * lightWeighting, fragmentColor.a);
if (specularUniform == 1)
{
if (dot(normalize(vTransformedNormal), lightDirection) > 0.99)
{
gl_FragColor = vec4(1.0, 1.0, 1.0, 1.0);
}
}
}
</script>
Subdivision Surface Algorithm
I was going to say something more about the Catmull-Clark subdivision surface algorithm and my implementation of that in JavaScript, but this article has gotten too long so I will leave that for a future article. But if you look into the code, you can see what's going on. I will just say that most of the action happens in a function called subdivisionSurfaceProcessFacet(), which does the work of subdividing a single facet by calculating a weighted average called a barycenter. The reason the algorithm is implemented in three functions, using timers, is so that I could draw a progress thermometer at the bottom of the screen. I had to do this since there isn't really threading in JavaScript. The algorithm takes a list of facets and replaces it with a list in which every facet has been replaced by four new facets. Note that care must be taken when the model has holes in it. Facets which lie on a border of such holes are treated as a special case.
function startSubdivision(solid)
{
informUser("Subdividing, please wait...");
subdivSurfaceLoopCounter = 0;
var facets = solid.facets;
solidToSubdivide = solid;
isSubdividing = true;
if (solid.nSubdivide == 0)
{
solid.previousFacetLists.push(solid.facets);
}
for (var i = 0; i < facets.length; i++)
{
facets[i].edges = getFacetLines(facets[i]);
facets[i].averagePoint3D = averageFacetPoint(facets[i].points);
}
findFacetNeighborsAndAdjacents(facets);
for (var i = 0; i < facets.length; i++)
{
var facet = facets[i];
for (var j = 0; j < facet.edges.length; j++)
{
var edge = facet.edges[j];
var list = [];
list.push(edge.start);
list.push(edge.end);
if (edge.parentFacet != -1 && edge.adjacentFacet != -1)
{
list.push(edge.parentFacet.averagePoint3D);
list.push(edge.adjacentFacet.averagePoint3D);
}
edge.edgePoint = averageFacetPoint(list);
}
}
subdivTimerId = setTimeout(subdivisionSurfaceProcessFacet, 0);
newSubdivFacets = [];
}
function subdivisionSurfaceProcessFacet()
{
var facet = solidToSubdivide.facets[subdivSurfaceLoopCounter];
var nEdge = 0;
var neighborsAndCorners = facetNeighborsPlusFacet(facet);
for (var j = 0; j < facet.points.length; j++)
{
var p = facet.points[j];
var facepoints = [];
var edgepoints = [];
var facetsTouchingPoint = findFacetsTouchingPoint(p, neighborsAndCorners);
for (var n = 0; n < facetsTouchingPoint.length; n++)
{
var f = facetsTouchingPoint[n];
facepoints.push(averageFacetPoint(f.points));
}
var edgesTouchingPoint = findEdgesTouchingPoint(p, facetsTouchingPoint);
for (var m = 0; m < edgesTouchingPoint.length; m++)
{
var l = edgesTouchingPoint[m];
edgepoints.push(midPoint3D(l.start, l.end));
}
var onBorder = false;
if (facepoints.length != edgepoints.length)
{
onBorder = true;
}
var F = averageFacetPoint(facepoints);
var R = averageFacetPoint(edgepoints);
var n = facepoints.length;
var barycenter = roundPoint(divPoint(plusPoints
(plusPoints(F, timesPoint(R, 2)), timesPoint(p, n - 3)), n));
var n1 = nEdge;
if (n1 > facet.edges.length - 1)
{
n1 = 0;
}
var n2 = n1 - 1;
if (n2 < 0)
{
n2 = facet.edges.length - 1;
}
if (onBorder)
{
var borderAverage = [];
var etp = edgesTouchingPoint;
for (var q = 0; q < etp.length; q++)
{
var l = etp[q];
if (lineIsOnBorder(l))
{
borderAverage.push(midPoint3D(l.start, l.end));
}
}
borderAverage.push(clonePoint3D(p));
barycenter = averageFacetPoint(borderAverage);
}
var newFacet = new Facet();
newFacet.points.push(clonePoint3D(facet.edges[n2].edgePoint));
newFacet.points.push(clonePoint3D(barycenter));
newFacet.points.push(clonePoint3D(facet.edges[n1].edgePoint));
newFacet.points.push(clonePoint3D(facet.averagePoint3D));
newSubdivFacets.push(newFacet);
newFacet.cube = solidToSubdivide;
nEdge++;
}
drawThermometer(solidToSubdivide.facets.length, subdivSurfaceLoopCounter);
subdivSurfaceLoopCounter++;
if (subdivSurfaceLoopCounter >= solidToSubdivide.facets.length)
{
clearInterval(subdivTimerId);
finishSubdivision(solidToSubdivide);
}
else
{
subdivTimerId = setTimeout(subdivisionSurfaceProcessFacet, 0);
}
}
function finishSubdivision(parentShape)
{
parentShape.nSubdivide++;
parentShape.facets = newSubdivFacets;
fuseFaster(parentShape);
selectedFacets = [];
selectedLines = [];
selectedVertexes = [];
sortFacets();
setFacetCount(parentShape);
isSubdividing = false;
alertUser("");
reloadSceneGL();
draw();
}
History
- 29th June, 2020: Initial version
