Math Function Tutor: Part 3

• Download project - 51.5 KB

Introduction

In Math Function Tutor Part 2, a Recursive Descent Parser (RDP) was introduced to evaluate expressions. An email I received about Part 2 pointed out that the RDP can be a bit difficult to understand. And as Herb Schildt himself says in C++ The Complete Reference on p. 967:

If you are a little confused at this point, don't feel bad.

In order to clarify the workings of the RDP, in this Part 3, I developed a small program that allows you to step through the RDP one method call at a time, helping you understand what is going on. Although it is not a substitute for studying the RDP code, I feel it will prove useful as it demonstrates how the RDP works.

A Console Program

For simplicity, this is a Windows Console project. I'm currently using an ASUS 24" monitor and have set the Console window width and height to 150 and 60. I've also run it on an HP laptop successfully. Depending on your color preferences and monitor, you can change the following in TestParserProgram.cs:

private const int ScreenWidth = 150;
private const int ScreenHeight = 60;
...
Console.SetBufferSize(ScreenWidth, ScreenHeight);
Console.ForegroundColor = ConsoleColor.Cyan;
Console.BackgroundColor = ConsoleColor.Black;

Using the Code

Download and extract the project, and open RDPInst.sln with Visual Studio. It consists of two projects:

1. RDPInstLib - the Recursive Descent Parser (RDP). This is the same RDP as in Part 2, with modifications that will be described below. The "Inst" is short for "Instrumented".
2. RDPInst - the main Console program for exercising the Instrumented Parser, TestParserProgram.cs.

Build the solution by pressing F6.

Stack Frame

The main modification to the RDP is the addition of a List<MyStackFrame> MyStackFrameList. The MyStackFrame class (I've given it this name so as not to confuse it with System.Diagnostics.StackFrame) consists of the items of interest while the RDP is evaluating an expression:

public class MyStackFrame
{
	public DateTime Timestamp { get; set; }
	public int StackLevel { get; set; }
	public String Op { get; set; }
	public String Method { get; set; }
	public String Token { get; set; }
	public RecursiveDescentParserInstrumented.TokenType TokenType { get; set; }
	public Double SaveResult { get; set; }
	public Double PartialResult { get; set; }
	public Double Result { get; set; }
	public int ExprNdx { get; set; }
}

As the name implies, a Recursive Descent Parser utilizes recursion, pushing values on the stack. As it does, a MyStackFrame object is created and added to the myStackFrameList. When the RDP has finished evaluating the expression, the TestParserProgram iterates over the list, in effect "playing back" the methods and values.

Introduction to Parsing

At the heart of a parser is its grammar, shown here in a notation known as EBNF:

1       <Expression> := [ "-" ]  <Term> { ("+" | "-")  <Term> }
2       <Term>       :=  <Factor> { ( "*" | "/" | "%" )  <Factor> }
3       <Factor>     :=  <RealNumber> | "("  <Expression> ")"
4       <RealNumber> := <Digit>{<Digit>} | {<Digit>} "." {<Digit>}
5       <Digit>      := "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9"

While this grammar definition can appear daunting if you are not familiar with EBNF, let's consider, the expression 1 + 2 * 3 and break it down into the grammar's symbols. Let's take a look at line 5 of the grammar. Keeping in mind the ":=" means "defined as", and the vertical bar, "|", means "or", line 5 is read as "A Digit is defined as a 0 or a 1 or a 2 - and so on - or a 9". In the language of EBNF grammars, the 0, 1, 2 ... 9 are known as a Terminal Symbols, and the <Digit> and other items within the < and > are Non-Terminal Symbols. Knowing that the curly braces in EBNF signify any number of items, line 4 could be read as "A <RealNumber> is defined as any number of <Digits>", or "A <RealNumber> is defined any number of <Digits>, a decimal point, followed by any number of <Digits>." Thus the 1, 2 and 3 in our expression are recognized as Non-Terminal Symbols called <RealNumbers>.

A <Factor> (line 3) is defined as either a <RealNumber> or a parenthesized expression; for our example a <Factor> will simply be a <RealNumber>. A <Term> (line 2) is defined as a <Factor> and optionally multiplied (or divided by, or modulo) another <Factor>, and in our case 2 * 3 is the first <Term>, and has a value of 6. The 1 is also a <RealNumber>, and will be our second <Term> (without the optional *, / or %). On the first line of the grammar, the <Expression> is defined as a <Term> plus (or minus) another <Term>. So our <Expression> is now simplified to the first <Term>, 6, plus the second <Term> 1, for the result of 7. Fortunately, Mr. Schildt has done the work of developing the code that recognizes this grammar!

In the code, the expression is evaluated from left to right, the parser breaking it into tokens by the method GetToken. In this example, there are 5 tokens, three of TokenType Number: 1, 2, 3, and two operands of TokenType Delimiter, the + and the *. Since the grammar specifies that the 2 and three must be multiplied before any addition, the 1 and + are placed on the stack, and after the 2 and 3 are multiplied (giving 6), the 1 is added for a final value of 7. Let's see this in action.

Running the Program

After building the program, press CTRL+F5 to "Start Without Debugging." A console window should appear with the prompt "Enter Expression For Instrumented Parser (Enter to quit)>" (be sure to set the height and width of the Console to the appropriate size.) Enter an expression to be parsed, and press the Enter key continuously until the expression is completed. As you press Enter, the program is iterating over the myStackFrameList. On the left-hand side, you can watch the method calls along with the result of the operation (addition, subtraction, exponentiation, and so on.) On the right-hand side is the stack; you can observe the numbers as they are pushed on the stack, then popped off when an operand, such as +, ^ or * is encountered, showing the current result. Note how the expression is shown in the lower-left with the caret pointing to the token that is currently being processed.

As an example, let's use the expression we looked at above. At the prompt in the lower left-hand corner of the screen, type 1 + 2 * 3 and press the Enter key 3 times. The screen shot below shows the result:

Note how the 1 is placed on the stack on the right-hand side. The caret in the lower-left hand side is pointing to the + in the expression. Now press Enter 3 more times and note how the 2 and 3 have been pushed on the stack. Press Enter once and see the result, 6, is placed on the top of the stack, replacing the 2 and 3. Recall from the grammar that the multiplication is performed before the addition. Press Enter twice and note how the 1 and 6 have been added to give 7, as illustrated in the screen shot below:

Pressing Enter again shows this is our final result, and at this point, you can enter another expression, or press Enter with no expression to quit.

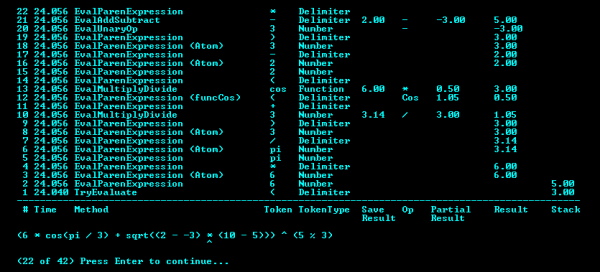
From left to right, the items displayed are:

1. The Stack Frame number
2. The Time Stamp in seconds and milliseconds when the method was executed
3. The Name of the method being executed
4. The Token being evaluated
5. The Token Type (see enum TokenType)
6. Save Result - the first result of previous EvalMultiplyDivide, EvalExponent or EvalUnaryOp
7. The arithmetic operator (+, -, *, /, %, ^)
8. Partial Result - the second result of previous EvalMultiplyDivide, EvalExponent or EvalUnaryOp
9. The Result of the arithmetic operation
10. The values on the stack

The screen shot at the top of this article shows a more complex expression, (6 * cos(pi / 3) + sqrt((2 - -3) * (10 - 5))) ^ (5 % 3), after pressing the Enter key 22 times. At this point, the 6 * cos(pi / 3) has been evaluated to 3 and is at the bottom of the stack. The 2 - -3 has been evaluated to 5 and is on top of the stack. Note that the minus sign before the 3 is the unary minus. If you continue to press the Enter key, you can see how the rest of the expression is evaluated, including the exponentiation and parenthesized expressions.

Conclusion

The grammar is the key to defining a language or expression parser. A hand-written Recursive Descent Parser like the one described in this article is one way to implement code to recognize the grammar. Alternatively, there are tools available, like ANTLR which can generate the code.

History

• Version 3.0.0.0