Descriptive Statistics and Data Normalization with CNTK and C#

Introduction

As you probably know, CNTK is Microsoft Cognitive Toolkit for deep learning. It is an open source library which is used by various Microsoft products. Also, the CNTK is a powerful library for developing custom ML solutions from various fields with different platforms and languages. What is also so powerful in the CNTK is the way of the implementation. In fact, the library is implemented as a series of computation graphs, which is fully elaborated into the sequence of steps performed in a deep neural network training.

Each CNTK compute graph is created with set of nodes where each node represents numerical (mathematical) operation. The edges between nodes in the graph represent data flow between operations. Such a representation allows CNTK to schedule computation on the underlying hardware GPU or CPU. The CNTK can dynamically analyze the graphs in order to optimize both latency and efficient use of resources. The most powerful part of this is the fact that the CNTK can calculate derivation of any constructed set of operations, which can be used for efficient learning process of the network parameters. The following image shows the core architecture of the CNTK.

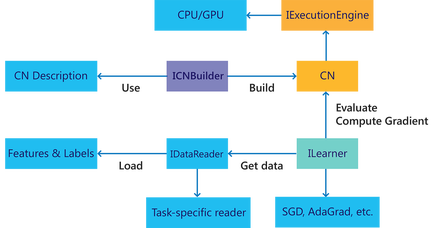
On the other hand, any operation can be executed on CPU or GPU with minimal code changes. In fact, we can implement a method which can automatically takes GPU computation if available. The CNTK is the first .NET library which provides .NET developers to develop GPU aware .NET applications.

What this exactly means is that with this powerful library, you can develop complex math computation directly to GPU in .NET using C#, which currently is not possible when using standard .NET library.

For this blog post, I will show how to calculate some of basic statistics operations on data set.

Say we have data set with 4 columns (features) and 20 rows (samples). The C# implementation of this 2D array is shown in the following code snippet:

static float[][] mData = new float[][] {
new float[] { 5.1f, 3.5f, 1.4f, 0.2f},
new float[] { 4.9f, 3.0f, 1.4f, 0.2f},
new float[] { 4.7f, 3.2f, 1.3f, 0.2f},
new float[] { 4.6f, 3.1f, 1.5f, 0.2f},
new float[] { 6.9f, 3.1f, 4.9f, 1.5f},
new float[] { 5.5f, 2.3f, 4.0f, 1.3f},
new float[] { 6.5f, 2.8f, 4.6f, 1.5f},
new float[] { 5.0f, 3.4f, 1.5f, 0.2f},
new float[] { 4.4f, 2.9f, 1.4f, 0.2f},
new float[] { 4.9f, 3.1f, 1.5f, 0.1f},
new float[] { 5.4f, 3.7f, 1.5f, 0.2f},
new float[] { 4.8f, 3.4f, 1.6f, 0.2f},
new float[] { 4.8f, 3.0f, 1.4f, 0.1f},
new float[] { 4.3f, 3.0f, 1.1f, 0.1f},
new float[] { 6.5f, 3.0f, 5.8f, 2.2f},
new float[] { 7.6f, 3.0f, 6.6f, 2.1f},
new float[] { 4.9f, 2.5f, 4.5f, 1.7f},
new float[] { 7.3f, 2.9f, 6.3f, 1.8f},
new float[] { 5.7f, 3.8f, 1.7f, 0.3f},
new float[] { 5.1f, 3.8f, 1.5f, 0.3f},};

If you want to play with CNTK and math calculation, you need some knowledge from Calculus, as well as vectors, matrix and tensors. Also in CNTK, any operation is performed as matrix operation, which may simplify for you the calculation process. In a standard way, you have to deal with multidimensional arrays during calculations. As per my knowledge, currently there is no .NET library which can perform math operation on GPU, which constrains the .NET platform for implementation of high performance applications.

If we want to compute average value, and standard deviation for each column, we can do that with CNTK in a very easy way. Once we compute those values, we can use them for normalizing the data set by computing standard score (Gauss Standardization).

The Gauss standardization is calculated by the flowing term:

,
where X- is column values, – column mean, and – standard deviation of the column.

For this example, we are going to perform three statistic operations,and the CNTK automatically provides us with ability to compute those values on GPU. This is very important in case you have data set with millions of rows, and computation can be performed in few milliseconds.

Any computation process in CNTK can be achieved in several steps:

1. Read data from external source or in-memory data
2. Define Value and Variable objects
3. Define Function for the calculation
4. Perform Evaluation of the function by passing the Variable and Value objects
5. Retrieve the result of the calculation and show the result

All the above steps are implemented in the following implementation:

using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using CNTK;
namespace DataNormalizationWithCNTK
{
    class Program
    {
       static float[][] mData = new float[][] {
        new float[] { 5.1f, 3.5f, 1.4f, 0.2f},
        new float[] { 4.9f, 3.0f, 1.4f, 0.2f},
        new float[] { 4.7f, 3.2f, 1.3f, 0.2f},
        new float[] { 4.6f, 3.1f, 1.5f, 0.2f},
        new float[] { 6.9f, 3.1f, 4.9f, 1.5f},
        new float[] { 5.5f, 2.3f, 4.0f, 1.3f},
        new float[] { 6.5f, 2.8f, 4.6f, 1.5f},
        new float[] { 5.0f, 3.4f, 1.5f, 0.2f},
        new float[] { 4.4f, 2.9f, 1.4f, 0.2f},
        new float[] { 4.9f, 3.1f, 1.5f, 0.1f},
        new float[] { 5.4f, 3.7f, 1.5f, 0.2f},
        new float[] { 4.8f, 3.4f, 1.6f, 0.2f},
        new float[] { 4.8f, 3.0f, 1.4f, 0.1f},
        new float[] { 4.3f, 3.0f, 1.1f, 0.1f},
        new float[] { 6.5f, 3.0f, 5.8f, 2.2f},
        new float[] { 7.6f, 3.0f, 6.6f, 2.1f},
        new float[] { 4.9f, 2.5f, 4.5f, 1.7f},
        new float[] { 7.3f, 2.9f, 6.3f, 1.8f},
        new float[] { 5.7f, 3.8f, 1.7f, 0.3f},
        new float[] { 5.1f, 3.8f, 1.5f, 0.3f},};
        static void Main(string[] args)
        {
            //define device where the calculation will executes
            var device = DeviceDescriptor.UseDefaultDevice();
 
            //print data to console
            Console.WriteLine($"X1,\tX2,\tX3,\tX4");
            Console.WriteLine($"-----,\t-----,\t-----,\t-----");
            foreach (var row in mData)
            {
                Console.WriteLine($"{row[0]},\t{row[1]},\t{row[2]},\t{row[3]}");
            }
            Console.WriteLine($"-----,\t-----,\t-----,\t-----");
 
            //convert data into enumerable list
            var data = mData.ToEnumerable<ienumerable<float>>(); 
             
            //assign the values 
            var vData = Value.CreateBatchOfSequences<float>(new int[] {4},data, device);
            //create variable to describe the data
            var features = Variable.InputVariable(vData.Shape, DataType.Float);
 
            //define mean function for the variable
            var mean =  CNTKLib.ReduceMean(features, new Axis(2));//Axis(2)- means calculate 
                                      //mean along the third axes which represent 4 features
             
            //map variables and data
            var inputDataMap = new Dictionary<variable, value="">() { { features, vData } };
            var meanDataMap = new Dictionary<variable, value="">() { { mean, null } };
 
            //mean calculation
            mean.Evaluate(inputDataMap,meanDataMap,device);
            //get result
            var meanValues = meanDataMap[mean].GetDenseData<float>(mean);
 
            Console.WriteLine($"");
            Console.WriteLine($"Average values for each features 
            x1={meanValues[0][0]},x2={meanValues[0][1]},x3={meanValues[0][2]},
            x4={meanValues[0][3]}");
 
            //Calculation of standard deviation
            var std = calculateStd(features);
            var stdDataMap = new Dictionary<variable, value="">() { { std, null } };
            //mean calculation
            std.Evaluate(inputDataMap, stdDataMap, device);
            //get result
            var stdValues = stdDataMap[std].GetDenseData<float>(std);
             
            Console.WriteLine($"");
            Console.WriteLine($"STD of features x1={stdValues[0][0]},
            x2={stdValues[0][1]},x3={stdValues[0][2]},x4={stdValues[0][3]}");
 
            //Once we have mean and std, we can calculate Standardized values for the data
            var gaussNormalization = 
                CNTKLib.ElementDivide(CNTKLib.Minus(features, mean), std);
            var gaussDataMap = new Dictionary<variable, value="">() 
                               { { gaussNormalization, null } };
            //mean calculation
            gaussNormalization.Evaluate(inputDataMap, gaussDataMap, device);
 
            //get result
            var normValues = 
                gaussDataMap[gaussNormalization].GetDenseData<float>(gaussNormalization);
            //print data to console
            Console.WriteLine($"-------------------------------------------");
            Console.WriteLine($"Normalized values for the above data set");
            Console.WriteLine($"");
            Console.WriteLine($"X1,\tX2,\tX3,\tX4");
            Console.WriteLine($"-----,\t-----,\t-----,\t-----");
            var row2 = normValues[0];
            for (int j = 0; j < 80; j += 4)
            {
                Console.WriteLine($"{row2[j]},
                                  \t{row2[j + 1]},\t{row2[j + 2]},\t{row2[j + 3]}");
            }
            Console.WriteLine($"-----,\t-----,\t-----,\t-----");
        }
 
        private static Function calculateStd(Variable features)
        {
            var mean = CNTKLib.ReduceMean(features,new Axis(2));
            var remainder = CNTKLib.Minus(features, mean);
            var squared = CNTKLib.Square(remainder);
            //the last dimension indicate the number of samples
            var n = new Constant(new NDShape(0), 
                    DataType.Float, features.Shape.Dimensions.Last()-1);
            var elm = CNTKLib.ElementDivide(squared, n);
            var sum = CNTKLib.ReduceSum(elm, new Axis(2));
            var stdVal = CNTKLib.Sqrt(sum);
            return stdVal;
        }
    }
 
    public static class ArrayExtensions
    {
        public static IEnumerable<t> ToEnumerable<t>(this Array target)
        {
            foreach (var item in target)
                yield return (T)item;
        }
    }
}

The output for the source code above should look like:

History

• 2^nd July, 2018: Initial version