Introduction
Perceptron is the simplest type of feed forward neural network. It was designed by Frank Rosenblatt as dichotomic classifier of two classes which are linearly separable. This means that the type of problems the network can solve must be linearly separable. Basic perceptron consists of 3 layers:
- Sensor layer
- Associative layer
- Output neuron
There are a number of inputs (xn) in sensor layer, weights (wn) and an output. Sometimes w0 is called bias and x0 = +1/-1 (In this case is x0=-1).
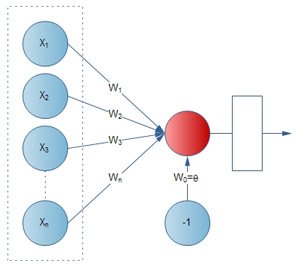
For every input on the perceptron (including bias), there is a corresponding weight. To calculate the output of the perceptron, every input is multiplied by its corresponding weight. Then weighted sum is computed of all inputs and fed through a limiter function that evaluates the final output of the perceptron.
The output of neuron is formed by activation of the output neuron, which is function of input:
| (1) | 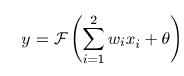 |
The activation function F can be linear so that we have a linear network, or nonlinear. In this example, I decided to use threshold (signum) function:
| (2) | 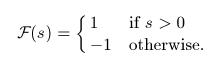 |
Output of network in this case is either +1 or -1 depending on the input. If the total input (weighted sum of all inputs) is positive, then the pattern belongs to class +1, otherwise to class -1. Because of this behavior, we can use perceptron for classification tasks.
Let's consider we have a perceptron with 2 inputs and we want to separate input patterns into 2 classes. In this case, the separation between the classes is straight line, given by equation:
| (3) | 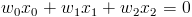 |
When we set x0=-1 and mark w0=?, then we can rewrite equation (3) into form:
| (4) | 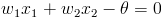 |
Here I will describe the learning method for perceptron. Learning method of perceptron is an iterative procedure that adjust the weights. A learning sample is presented to the network. For each weight, the new value is computed by adding a correction to the old value. The threshold is updated in the same way:
| (5) | 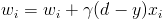
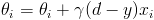
|
where y is output of perceptron, d is desired output and ? is the learning parameter.
Using the Program
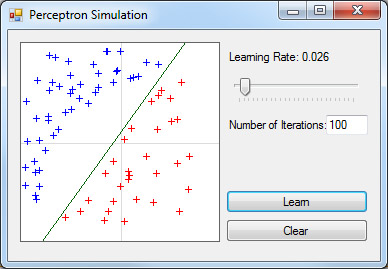
When you run the program, you see area where you can input samples. Clicking by left button on this area, you will add first class sample (blue cross). Clicking by right button on this area, you will add first class sample (red cross). Samples are added to the samples list. You can also set learning rate and number of iterations. When you have set all these values, you can click on Learn button to start learning.
Using the Code
All samples are stored in generic list samples which holds only Sample class objects.
public class Sample
{
double x1;
double x2;
double cls;
public Sample(double x1, double x2, int cls)
{
this.x1 = x1;
this.x2 = x2;
this.cls = cls;
}
public double X1
{
get { return x1; }
set { this.x1 = value; }
}
public double X2
{
get { return x2; }
set { this.x2 = value; }
}
public double Class
{
get { return cls; }
set { this.cls = value; }
}
}
Before running a learning of perceptron is important to set learning rate and number of iterations. Perceptron has one great property. If solution exists, perceptron always find it but problem occurs, when solution does not exist. In this case, perceptron will try to find the solution in infinity loop and to avoid this, it is better to set maximum number of iterations.
The next step is to assign random values for weights (w0, w1 and w2).
Random rnd = new Random();
w0 = rnd.NextDouble();
w1 = rnd.NextDouble();
w2 = rnd.NextDouble();
When random values are assigned to weights, we can loop through samples and compute output for every sample and compare it with desired output.
double x1 = samples[i].X1;
double x2 = samples[i].X2;
int y;
if (((w1 * x1) + (w2 * x2) - w0) < 0)
{
y = -1;
}
else
{
y = 1;
}
I decided to set x0=-1 and for this reason, the output of perceptron is given by equation: y=w1*w1+w2*w2-w0. When perceptron output and desired output doesn’t match, we must compute new weights:
if (y != samples[i].Class)
{
error = true;
w0 = w0 + alpha * (samples[i].Class - y) * x0 / 2;
w1 = w1 + alpha * (samples[i].Class - y) * x1 / 2;
w2 = w2 + alpha * (samples[i].Class - y) * x2 / 2;
}
Y is output of perceptron and samples[i].Class is desired output. The last 2 steps (looping through samples and computing new weights), we must repeat while the error variable is <> 0 and current number of iterations (iterations) is less than maxIterations.
int i;
int iterations = 0;
bool error = true;
maxIterations = int.Parse(txtIterations.Text);
Random rnd = new Random();
w0 = rnd.NextDouble();
w1 = rnd.NextDouble();
w2 = rnd.NextDouble();
alpha = (double)trackLearningRate.Value / 1000;
while (error && iterations < maxIterations)
{
error = false;
for (i = 0; i <= samples.Count - 1; i++)
{
double x1 = samples[i].X1;
double x2 = samples[i].X2;
int y;
if (((w1 * x1) + (w2 * x2) - w0) < 0)
{
y = -1;
}
else
{
y = 1;
}
if (y != samples[i].Class)
{
error = true;
w0 = w0 + alpha * (samples[i].Class - y) * x0 / 2;
w1 = w1 + alpha * (samples[i].Class - y) * x1 / 2;
w2 = w2 + alpha * (samples[i].Class - y) * x2 / 2;
}
}
objGraphics.Clear(Color.White);
DrawSeparationLine();
iterations++;
}
Function DrawSeparationLine draws separation line of 2 classes.
History
- 07 Nov 2010 - Original version posted
