I created this library because I needed to handle units of measure, mainly the ones from the SI (International System of Units) ones (but also possibly more esoteric ones) and quantities in a system where the quantities and their units must be persisted in a database and where different contexts of units can coexist (think multi-tenancy). In the article I go over: a bit about the metric system and dimensional equation, standard and binary prefixes, handling aliases, normalizing units, and parsing.
Introduction
This is my first article on Code Project. Too often, I work on too big, too specific or too useless projects, but this one is small and interesting enough to be here. I spent 9 days on it and took the time, for each of them, to log my activity. I'd like this article to be read as a kind of "travel diary in software development". Each day led to an implementation and its unit tests, some days were about refactoring (and sometimes rolling back previous code): a typical developer's life.
Enough about the form. What about the content?
I needed to handle units of measure, mainly the ones from the SI (International System of Units) ones (but also possibly more esoteric ones) and quantities in a system where the quantities and their units must be persisted in a database and where different "contexts of units" can coexist (think multi-tenancy).
Background
The existing solutions I found for C# were all interesting but didn't satisfy me. Some words about two of them:
If you look a little bit farther, you'll find F# and its standard units of measure: http://docs.microsoft.com/en-us/dotnet/fsharp/language-reference/units-of-measure. Functional shines! However...
Quote:
Units at Runtime
Units of measure are used for static type checking. When floating point values are compiled, the units of measure are eliminated, so the units are lost at run time. Therefore, any attempt to implement functionality that depends on checking the units at run time is not possible. For example, implementing a ToString function to print out the units is not possible.
(http://docs.microsoft.com/en-us/dotnet/fsharp/language-reference/units-of-measure#units-at-runtime)
My need is more "dynamic", more data-driven (a totally new unit of measure can be created during the import of a CSV or from a JSON returned by a Web API) and somehow lighter than what I found (the end result is a netstandard 2.0 DLL of... 32KB).
Limitations
A lot of existing libraries support multi-lingual, culture dependent textual representation of units. This one doesn't. Rendering of units and quantities is a UI concern and should be done there (just like date and time). Similarly, non linear conversions like the classical °C to °F are out of the scope. For temperature, the SI unit is the Kelvin and displaying or entering Centigrades or Farenheits must be handled as a UI preference (just like the culture).
Last but not least, money: converting $ in € is out of scope. Currencies can be defined as Units that are independent of each other. You can manipulate quantities in "$/m²" and "€/m²" (in a real-estate management application), but the actual change rate (and conversion) must be done elsewhere.
Summary
To understand this, one needs to know a bit about the metric system and dimensional equation. Please read https://en.wikipedia.org/wiki/Metric_system and https://en.wikipedia.org/wiki/Dimensional_analysis.
We use the 7 base units of the SI (https://en.wikipedia.org/wiki/International_System_of_Units) as a starting point: these are the FundamentalMeasureUnit. A fundamental unit is semantically equivalent (for us) to a dimension. We define 3 fundamental units (dimensions) and new ones can be dynamically added to the system as required (for instance “$” and/or “€”, “£”, etc.). Note that each currency would be a dimension. Converting a quantity of “$” to “€” is not in the scope of this library, it must be done externally.
The three fundamental units we define by default are:
public static readonly FundamentalMeasureUnit None;
public static readonly FundamentalMeasureUnit Unit;
public static readonly FundamentalMeasureUnit Bit;
These fundamental units actually are BasicMeasureUnit with their Exponent set to 1. The BasicMeasureUnit is bound to a FundamentalMeasureUnit with an exponent: they handle the basic items of a dimensional equation m^2, s^-1, etc.
NormalizedMeasureUnit captures a list of one or more BasicMeasureUnit. The list is normalized by decreasing exponents and then by fundamental unit’s name lexicographic order.
For the moment, a simple hierarchy is enough with the MeasureUnit abstract class at its root:
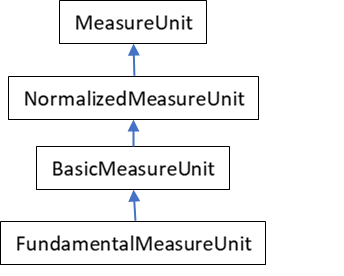
Figure: Initial model
With this simple model and the help of C# operators overload (*, / and ^), one can achieve this kind of funny dimensional game (from https://en.wikipedia.org/wiki/SI_derived_unit):
var metre = MeasureUnit.Metre;
var second = MeasureUnit.Second;
var kilogram = MeasureUnit.Kilogram;
var ampere = MeasureUnit.Ampere;
var candela = MeasureUnit.Candela;
var squaredMeter = metre^2;
var hertz = MeasureUnit.None / second;
hertz.Abbreviation.Should().Be( "s-1" );
var rad = metre * (metre ^ -1);
rad.Should().BeSameAs( MeasureUnit.None );
var steradian = squaredMeter / squaredMeter;
steradian.Should().BeSameAs( MeasureUnit.None );
var newton = kilogram * metre * (second ^ -2);
newton.Abbreviation.Should().Be( "kg.m.s-2" );
var pascal = newton / squaredMeter;
pascal.Abbreviation.Should().Be( "kg.m-1.s-2" );
var joule = newton * metre;
var watt = joule / second;
var coulomb = ampere * second;
var volt = watt / ampere;
var volt2 = joule / coulomb;
volt.Should().BeSameAs( volt2 );
volt.Abbreviation.Should().Be( "m2.kg.A-1.s-3" );
var farad = coulomb / volt;
farad.Abbreviation.Should().Be( "s4.A2.kg-1.m-2" );
var ohm = volt / ampere;
ohm.Abbreviation.Should().Be( "m2.kg.A-2.s-3" );
var farad2 = second / ohm;
farad2.Should().BeSameAs( farad );
var siemens = MeasureUnit.None / ohm;
var siemens2 = ampere / volt;
siemens.Should().BeSameAs( siemens2 );
siemens.Abbreviation.Should().Be( "s3.A2.kg-1.m-2" );
var weber = joule / ampere;
var tesla = volt * second / squaredMeter;
var tesla2 = weber / squaredMeter;
var tesla3 = newton / (ampere * metre);
tesla2.Should().BeSameAs( tesla );
tesla3.Should().BeSameAs( tesla );
tesla.Abbreviation.Should().Be( "kg.A-1.s-2" );
var henry = ohm * second;
var henry2 = volt * second / ampere;
var henry3 = weber / ampere;
henry2.Should().BeSameAs( henry );
henry3.Should().BeSameAs( henry );
henry.Abbreviation.Should().Be( "m2.kg.A-2.s-2" );
var lumen = candela * steradian;
var lux = lumen / squaredMeter;
lux.Abbreviation.Should().Be( "cd.m-2" );
Important note: The code above shows that the objects are actually the same object (reference equality) when they define the same unit of measure. This is one of the goals of this library: units must be fully normalized and cached even if new unit of measure can be dynamically created at any time. This is achieved thanks to a ConcurrentDictionary, the “Abbreviation” property of the measures being the key.
Even if it works like a charm and is funny, this is not enough. We must handle:
- Prefixes: Standard ones like
“d”/”Deci” like in “dm”/”Decimeter” or “m”/”Milli” like in “mm”/”Millimeter”. See https://en.wikipedia.org/wiki/Metric_prefix and since we added bit, we should also handle binary prefixes (see https://en.wikipedia.org/wiki/Binary_prefix): “Ki”/”Kibbi” like “Kib”/”KibiBit”.
Introducing this is not as easy as it seems. We must be able to transparently handle equivalence like, for instance, the fact that m.s-2 (metre per squared second, i.e., an acceleration) is the same as μm.ms-2 (micrometer per squared milliseconds).
- Derived units: A Derived Unit is like an alias, for instance
“l”/”Liter” is the same as “dm3”, i.e., 10-3 m3.
Some of the actually used units introduce a factor (that does not fit into a simple exponentiation like the liter).
For instance:
- A newton (N): its definition directly uses fundamental units: 1 N = 1 kg.m.s-2
- A dyne (dyn) is defined with the newton: 1 dyn = 10-5 N
- A kilopond (kp) is: 1 kp = 9.80665 N
This definitely requires a more complex model.
Let’s start with standard and binary prefixes. These prefixes (“G”/”Giga”, “k”/”Kilo”, “K”/”Kibi”, “m”/”Milli”, etc.) apply only to non-exponentiated units like the fundamental units and can be used wherever a fundamental unit is used.
A deci(squared metre) is NOT Valid, however a squared(decimetre) is.
To properly model this, we refine a little bit our model by introducing a PrefixedMeasureUnit at the same (lowest) level as the FundamentalMeasureUnit.
To unify these two types, we introduce a new AtomicMeasureUnit class that is the base class of FundamentalMeasureUnit and PrefixedMeasureUnit.
The NormalizedMeasureUnit now handles one or more (possibly exponentiated) fundamental units as well as PrefixedMeasureUnit that are not “fundamentals”. Its name (“normalized”) is no more accurate: we change it to just be a CombinedMeasureUnit that better reflects what it is.
Since we are dealing with (bad) names, the “Basic measure unit” does not convey a clear idea of what it is. We rename the BasicMeasureUnit to be ExponentMeasureUnit.
The new class diagram is:

Figure: Introducing prefixes and better naming
The standard S.I. prefixes (all of them) are captured and exposed by the MeasureStandardPrefix class through a set of singletons. This set is not extensible (you can’t define your own prefix).
These prefixes can be applied to any AtomicMeasureUnit to obtain another AtomicMeasureUnit since the result of the prefix application may actually be a prefixed unit or a fundamental unit.
var centimetre = MeasureStandardPrefix.Centi.On( MeasureUnit.Metre );
centimetre.Abbreviation.Should().Be( "cm" );
centimetre.Name.Should().Be( "Centimetre" );
If we apply the Hecto prefix to this centimetre, we obtain the (fundamental) metre.
var hectocentimetre = MeasureStandardPrefix.Hecto.On( centimetre );
hectocentimetre.Should().BeSameAs( MeasureUnit.Metre );
Below is the whole test for this new game:
[Test]
public void playing_with_decimetre_and_centimeter()
{
var decimetre = MeasureStandardPrefix.Deci.On( MeasureUnit.Metre );
decimetre.Abbreviation.Should().Be( "dm" );
decimetre.Name.Should().Be( "Decimetre" );
var decimetreCube = decimetre ^ 3;
decimetreCube.Abbreviation.Should().Be( "dm3" );
decimetreCube.Name.Should().Be( "Decimetre^3" );
var centimetre = MeasureStandardPrefix.Centi.On( MeasureUnit.Metre );
centimetre.Abbreviation.Should().Be( "cm" );
centimetre.Name.Should().Be( "Centimetre" );
var decidecimetre = MeasureStandardPrefix.Deci.On( decimetre );
decidecimetre.Should().BeSameAs( centimetre );
var hectocentimetre = MeasureStandardPrefix.Hecto.On( centimetre );
hectocentimetre.Should().BeSameAs( MeasureUnit.Metre );
var kilocentimeter = MeasureStandardPrefix.Kilo.On( centimetre );
kilocentimeter.Abbreviation.Should().Be( "dam" );
var decametre = MeasureStandardPrefix.Deca.On( MeasureUnit.Metre );
decametre.Should().BeSameAs( decametre );
}
To conclude this second day, one needs to consider a not-so-edge-case: standard prefixes are not “complete” enough to be safely used. What happens if you want the “Deci” (10-1) of a “Giga” (109)? There is no prefix available for 108. Similar question: what is a Kilo Yotta (Yotta is the biggest prefix: 1024).
Note that you may not ask it directly, but this may happen indirectly in a complex system. We must be able to cope with these cases, even if we’ll always try to eventually avoid such “intermediate” prefixes.
The idea is to introduce an “adjustment factor” to our PrefixedMeasureUnit. This adjustment is a ExpFactor that enables us to handle exponents without relying on floating point types (and their intrinsic limitations).
public struct ExpFactor : IComparable<ExpFactor>, IEquatable<ExpFactor>
{
public static readonly ExpFactor Neutral;
public readonly int Exp2;
public readonly int Exp10;
public ExpFactor Power( int p ) => new ExpFactor( Exp2 * p, Exp10 * p );
public ExpFactor Multiply( ExpFactor x ) => new ExpFactor( Exp2 + x.Exp2, Exp10 + x.Exp10 );
public ExpFactor DivideBy( ExpFactor x ) => new ExpFactor( Exp2 - x.Exp2, Exp10 - x.Exp10 );
}
Note: There is a little bit more code in the struct above, we only show here the most relevant aspects.
There are two exponents: one in base 2 (since we support binary prefixes) and the other in base 10 for metric prefixes.
This allows us to generate “intermediate prefixes” or “out-of-bound” prefixes as required and keep the whole system safe and coherent as long as we find a way to express/show/recognize these beasts.
If an adjustment factor is not the neutral one, it appears in the abbreviation and name of the unit of measure: “(10^-1)Gm”/”(10^-1)Gigameter” will be the “Decigigametre” that do not exist. Of course, you will never meet the “(10^-1)cm” since this is a “mm”/”Millimetre”!
Note the syntax: We have deliberately chosen a syntax that differs from the standard exponent (with the base and the caret ^) so that these beasts can easily been spotted.
Here are the tests that conclude this Day 2:
[Test]
public void playing_with_adjustment_factors()
{
var gigametre = MeasureStandardPrefix.Giga[MeasureUnit.Metre];
gigametre.Abbreviation.Should().Be( "Gm" );
gigametre.Name.Should().Be( "Gigametre" );
var decigigametre = MeasureStandardPrefix.Deci[gigametre];
decigigametre.Abbreviation.Should().Be( "(10^-1)Gm" );
decigigametre.Name.Should().Be( "(10^-1)Gigametre" );
var decidecigigametre = MeasureStandardPrefix.Deci[decigigametre];
decidecigigametre.Abbreviation.Should().Be( "(10^1)Mm" );
decidecigigametre.Name.Should().Be( "(10^1)Megametre" );
var decidecidecigigametre = MeasureStandardPrefix.Deci[decidecigigametre];
decidecidecigigametre.Abbreviation.Should().Be( "Mm" );
decidecidecigigametre.Name.Should().Be( "Megametre" );
}
[Test]
public void out_of_bounds_adjustment_factors()
{
var yottametre = MeasureStandardPrefix.Yotta[MeasureUnit.Metre];
var lotOfMetre = MeasureStandardPrefix.Hecto[yottametre];
lotOfMetre.Abbreviation.Should().Be( "(10^2)Ym" );
var evenMore = MeasureStandardPrefix.Deca[lotOfMetre];
evenMore.Abbreviation.Should().Be( "(10^3)Ym" );
var backToReality = MeasureStandardPrefix.Yocto[evenMore];
backToReality.Abbreviation.Should().Be( "km" );
var belowTheAtom = MeasureStandardPrefix.Yocto[backToReality];
belowTheAtom.Abbreviation.Should().Be( "zm" );
belowTheAtom.Name.Should().Be( "Zeptometre", "The Zeptometre is 10^-21 metre." );
var decizettametre = MeasureStandardPrefix.Deci[belowTheAtom];
decizettametre.Abbreviation.Should().Be( "(10^-1)zm" );
var decidecizettametre = MeasureStandardPrefix.Deci[decizettametre];
decidecizettametre.Abbreviation.Should().Be( "(10^1)ym" );
var yoctometre = MeasureStandardPrefix.Deci[decidecizettametre];
yoctometre.Abbreviation.Should().Be( "ym" );
var below1 = MeasureStandardPrefix.Deci[yoctometre];
below1.Abbreviation.Should().Be( "(10^-1)ym" );
var below2 = MeasureStandardPrefix.Deci[below1];
below2.Abbreviation.Should().Be( "(10^-2)ym" );
}
It is time now to handle aliases and eventually find a way to normalize units so that we can actually use them to compute quantities.
The Kilogram Exception and the Byte
Currently, there is no way to manipulate grams since for the moment a gram is a Milli Kilogram: Kilogram is the official standard unit of weight. You don’t want so see the “mkg” unit!
Introducing an alias for the “mkg” (as a “g”/”Gram”) would imply to cope with this exception in too much code location. It is definitely easier to “cheat” and define the Gram as being the fundamental unit instead of the Kilogram. The Kilogram is now defined in the MeasureUnit type initializer as a PrefixedMeasureUnit (and still exposed as a static property):
public static readonly PrefixedMeasureUnit Kilogram;
public static readonly FundamentalMeasureUnit Gram;
In the Type initializer (static private constructor):
Kilogram = RegisterPrefixed( ExpFactor.Neutral, MeasureStandardPrefix.Kilo, Gram );
Byte is also exposed as a static field on the MeasureUnit class. It uses the new AliasMeasureUnit class that now enables us to create new named units from other ones:
public static readonly AliasMeasureUnit Byte;
and:
Byte = new AliasMeasureUnit( "B", "Byte", new FullFactor( new ExpFactor(3,0) ), Bit );
Defining New Units
The new alias and the original fundamental units are the only two ways to explicitly define new unit of measure:
public static AliasMeasureUnit DefineAlias(
string abbreviation,
string name,
FullFactor definitionFactor,
CombinedMeasureUnit definition ) { … }
public static FundamentalMeasureUnit DefineFundamental( string abbreviation, string name ) { … }
The FullFactor that appears in the DefineAlias is a simple extension to the ExpFactor previously described that adds a simple Factor field to it. We use a double for the moment but what we should use here is a rational such as the one provided by https://www.nuget.org/packages/Rationals/ (that seems a nice project).
A FullFactor describes a simple linear adjustment of the definition units. Thanks to it, we can now define the newton, the dyne and the kilopound (from https://en.wikipedia.org/wiki/Newton_(unit)):
- A newton (N): its definition directly uses fundamental units: 1 N = 1 kg.m.s-2
- A dyne (dyn) is defined with the newton: 1 dyn = 10-5 N
- A kilopond (kp) is: 1 kp = 9.80665 N
using static CK.Core.MeasureUnit;
…
var kg = Kilogram;
var m = Metre;
var s = Second;
var newton = DefineAlias( "N", "Newton", FullFactor.Neutral, kg * m * (s ^ -2) );
var dyne = DefineAlias( "dyn", "Dyne", new ExpFactor( 0, -5 ), newton );
var kilopound = DefineAlias( "kp", "Kilopound", 9.80665, newton );
var newtonPerDyne = newton / dyne;
newtonPerDyne.Abbreviation.Should().Be( "N.dyn-1" );
Note
- To shorten the code above, we have used the using
static CK.Core.MeasureUnit FullFactor defines implicit conversion operators from double and ExpFactor. We could have defined the newton in an even more simple way:
var newton = DefineAlias( "N", "Newton", 1.0, kg * m * (s ^ -2) );
So far so good… but… what is the actual unit of “N.dyn-1”?
You may be surprised but it could be “radian” (or “steradian“) since this has actually no unit: it is Measure.None (just like radian and steradian that are not actual units).
We are now ready to use these units to calculate quantities!
A Quantity is simply a numerical value (int, float, double, rational, big integer, etc.) associated to its unit of measure.
One of the goals of this library is to help computing such quantities like:

The value of r above is 2.105. That is 2.105 MeasureUnit.None for us: the N.dyn-1 must resolve to the dimensionless unit and to the factor that links them.
Before manipulating quantities, they must be first promoted/aligned to the same measure of units. You can always multiply/divide quantities (whatever their dimensions are) by simply creating the resulting dimension: 10 m x 40 min = 400 m.min.
However, to add or subtract 2 quantities, they must have exactly the same unit: 2 m2 + 3 m2 = 5m2 or 2 m2 + 3 cm2 that is perfectly valid and equals to 20003 cm2 (or 2.0003 m2 as you prefer).
Before tackling this aspect, we need a little bit of refactoring. Current model has the MeasureUnit as a base abstract class of all units. However, the only actual specialization is the CombinedMeasureUnit and it appears that this is all what is needed (this was not obvious on day 1, this indirection seemed useful at this time). We can now simplify the model by acting that a MeasureUnit is always a CombinedMeasureUnit. The latter is gone, merged into the MeasureUnit (that is getting bigger) and to keep code clean, it is split in partial files.
The final class diagram is:

Figure: Final model
We could have merged Exponent and Atomic, but we didn't and don’t want to. For two reasons:
1 - This (see Day 1) is currently not possible and we want to keep this:
var decimetreCube = decimetre ^ 3;
decimetreCube.Abbreviation.Should().Be( "dm3" );
decimetreCube.Name.Should().Be( "Decimetre^3" );
2 - This would make the code less “type safe” and hence a little bit more “complex” to write and to understand.
Refactor done. Let’s go back to the task of the day: the normalization.
There is here an obvious choice: the FundamentalMeasureUnit is by design the canonical form of each and every mono-dimensional unit of measure. When multiple dimensions are involved, there is one composite MeasureUnit that contains only atomic (or power of) FundamentalMeasureUnit (i.e., no more aliases or prefixed units).
From any MeasureUnit to its Canonical form, we can calculate (once for all) the FullFactor that maps the unit to it.
Introducing a new class is useless for this. It is easier to introduce this into our model by adding 3 properties to the MeasureUnit base class:
public bool IsNormalized { get; }
public FullFactor NormalizationFactor { get; }
public MeasureUnit Normalization { get; }
And it works!
Tests below show the conversion of dm^2 and cm^2 to m2, demonstrates the fact that m.s-2 (metre per squared second, i.e., an acceleration) is the same as μm.ms-2 (micrometer per squared milliseconds) and that 1 m/s is around 0.277778 km/h!
[Test]
public void basic_normalization_with_prefix()
{
var metre = MeasureUnit.Metre;
var squaredMeter = metre ^ 2;
squaredMeter.Normalization.Should().Be( squaredMeter );
var decimeter = MeasureStandardPrefix.Deci[metre];
var squaredDecimeter = decimeter ^ 2;
squaredDecimeter.Normalization.Should().Be( squaredMeter );
squaredDecimeter.NormalizationFactor
.Should().Be( new FullFactor( new ExpFactor( 0, -2 ) ), "1 dm2 = 10-2 m2" );
var centimeter = MeasureStandardPrefix.Centi[metre];
var squaredCentimeter = centimeter ^ 2;
squaredCentimeter.Normalization.Should().Be( squaredMeter );
squaredCentimeter.NormalizationFactor
.Should().Be( new FullFactor( new ExpFactor( 0, -4 ) ), "1 cm2 = 10-4 m2" );
}
[Test]
public void equivalent_combined_units()
{
var metre = MeasureUnit.Metre;
var second = MeasureUnit.Second;
var acceleration = metre / (second ^ 2);
acceleration.IsNormalized.Should().BeTrue();
var micrometre = MeasureStandardPrefix.Micro[metre];
var millisecond = MeasureStandardPrefix.Milli[second];
var acceleration2 = micrometre / (millisecond ^ 2);
acceleration2.IsNormalized.Should().BeFalse();
acceleration2.Normalization.Should().BeSameAs( acceleration );
acceleration2.NormalizationFactor.Should().Be( FullFactor.Neutral );
}
[Test]
public void combined_units_with_factor()
{
var metre = MeasureUnit.Metre;
var second = MeasureUnit.Second;
var speed = metre / second;
speed.IsNormalized.Should().BeTrue();
var kilometre = MeasureStandardPrefix.Kilo[metre];
var hour = MeasureUnit.DefineAlias( "h", "Hour", 60*60, second );
var speed2 = kilometre / hour;
speed2.IsNormalized.Should().BeFalse();
speed2.Normalization.Should().BeSameAs( speed );
speed2.NormalizationFactor.ToDouble()
.Should().BeApproximately( 0.2777777778, 1e-10, "1 m/s = 0.277778 km/h" );
}
We have no more time today to detail the (minimalist) code that does this “magic” (what is actually magic is how minimal it is 😊). We’ll talk about this tomorrow.
Yesterday, while implementing the normalization, I realized that it was quite easy to separate the two notions of Canonical/Normalized unit of measure and FundamentalMeasureUnit that I initially considered as being the same thing. Thanks to this, the “kilogram exception” is no more an exception, and the cherry on the cake is that this feature is now available when you define a fundamental unit:
normalizedPrefix"
Optional prefix to be used for units where the normalized unit should not be the
FundamentalMeasureUnit but one of its PrefixedMeasureUnit.
This is the case for the "g"/"Gram" and the "kg"/"Kilogram".
Defaults to MeasureStandardPrefix.None: by default a fundamental unit is the
normalized one.
public static FundamentalMeasureUnit DefineFundamental(
string abbreviation,
string name,
MeasureStandardPrefix normalizedPrefix = null )
This new normalization behavior is now compliant with the S.I:
var metre = MeasureUnit.Metre;
var second = MeasureUnit.Second;
var kilogram = MeasureUnit.Kilogram;
var newton = kilogram * metre * (second ^ -2);
newton.Abbreviation.Should().Be( "kg.m.s-2" );
newton.Normalization.Abbreviation.Should().Be( "kg.m.s-2" );
newton.NormalizationFactor.Should().Be( FullFactor.Neutral );
It’s time to explain the normalization code. The actual normalized form is computed on-demand if, and only if, the unit is not (by construction) defined as THE normalized form and if it has not been already computed:
public bool IsNormalized => _normalization == this;
public FullFactor NormalizationFactor
{
get
{
if( _normalization == null )
{
(_normalization, _normalizationFactor) = GetNormalization();
}
return _normalizationFactor;
}
}
public MeasureUnit Normalization
{
get
{
if( _normalization == null )
{
(_normalization, _normalizationFactor) = GetNormalization();
}
return _normalization;
}
}
We are using value tuple here to return both the factor and the normalized unit from the actual computation. At the top level of the MeasureUnit, the potentially multiple units’ normalized forms are combined into one list of deduplicated units AND, at the same time, the final normalization factor is computed by multiplying all the normalization factors with an initial neutral one.
The Combinator is a small private struct that encapsulates deduplication. It has been developed on Day 1 (with some refactoring since its creation) and is quite simple (its code can be found here: https://github.com/Invenietis/CK-UnitsOfMeasure/blob/master/CK.UnitsOfMeasure/MeasureUnit.Combinator.cs).
private protected virtual (MeasureUnit, FullFactor) GetNormalization()
{
Combinator measures = new Combinator( null );
var f = _units.Aggregate( FullFactor.Neutral, ( acc, m ) =>
{
measures.Add( m.Normalization.MeasureUnits );
return acc.Multiply( m.NormalizationFactor );
} );
return (measures.GetResult(), f);
}
This is the general implementation, for the combined unit of measure. Exponent and Atomic units override this behavior and this is, up to me, a demonstration of the beauty of the good old standard object paradigm.
The normalized form of an ExponentMeasureUnit is the normalized form of its atomic measure elevated to its own power. And its normalization factor is one of its atomic measures also elevated to its own power.
private protected override (MeasureUnit, FullFactor) GetNormalization()
{
return (
AtomicMeasureUnit.Normalization.Power( Exponent ),
AtomicMeasureUnit.NormalizationFactor.Power( Exponent )
);
}
For the AliasMeasureUnit, it is even simpler: its normalized form is one of its definitions and its normalization factor is multiplied by its own DefinitionFactor.
private protected override (MeasureUnit, FullFactor) GetNormalization()
{
return (
Definition.Normalization,
Definition.NormalizationFactor.Multiply( DefinitionFactor )
);
}
And finally, the PrefixedMeasureUnit computes its normalization factor by applying its prefix’ factor and its adjustment factor (the adjustment factor kindly handles silly prefixes like “DeciGiga” – see Day 2).
private protected override (MeasureUnit, FullFactor) GetNormalization()
{
return (
AtomicMeasureUnit.Normalization,
AtomicMeasureUnit.NormalizationFactor
.Multiply( Prefix.Factor )
.Multiply( AdjustmentFactor )
);
}
And this is it!
You may wonder “what about thread safety? This seems absolutely not thread safe!”.
This is totally thread-safe (the whole library is totally thread-safe). But since it could be quite a long discussion, I’ll talk about this later. I’m thrilled to start implementing quantities…
Quantity is a simple immutable value type that simply combines a double value and a unit. Operations on quantities are straightforward to implement. Below is the core of the Quantity type:
public struct Quantity
{
public readonly double Value;
public readonly MeasureUnit Unit;
public Quantity( double v, MeasureUnit u )
{
Value = v;
Unit = u;
}
public Quantity Multiply( Quantity q ) => new Quantity( Value * q.Value, Unit * q.Unit );
public Quantity DivideBy( Quantity q ) => new Quantity( Value / q.Value, Unit / q.Unit );
public Quantity Invert() => new Quantity( 1.0 / Value, Unit.Invert() );
public Quantity Power( int exp ) =>
new Quantity( Math.Pow( Value, exp ), Unit.Power( exp ) );
public bool CanConvertTo( MeasureUnit u ) => Unit.Normalization == u.Normalization;
public Quantity ConvertTo( MeasureUnit u )
{
if( !CanConvertTo( u ) )
{
throw new ArgumentException( $"Can not convert from '{Unit}' to '{u}'." );
}
FullFactor ratio = Unit.NormalizationFactor.DivideBy( u.NormalizationFactor );
return new Quantity( Value * ratio.ToDouble(), u );
}
public static Quantity operator /( Quantity o1, Quantity o2 ) => o1.DivideBy( o2 );
public static Quantity operator *( Quantity o1, Quantity o2 ) => o1.Multiply( o2 );
public static Quantity operator ^( Quantity o, int exp ) => o.Power( exp );
public string ToString( IFormatProvider formatProvider ) =>
Value.ToString( formatProvider )
+ " " + Unit.ToString();
public override string ToString() => $"{Value} {Unit}";
}
With the help of a WithUnit extension methods on int and double (I generally avoid polluting basic types with extension methods, but here I think it makes sense), it works:
[Test]
public void simple_operations()
{
var metre = MeasureUnit.Metre;
var second = MeasureUnit.Second;
var kilometre = MeasureStandardPrefix.Kilo[metre];
var minute = MeasureUnit.DefineAlias( "min", "Minute", 60, second );
var hour = MeasureUnit.DefineAlias( "h", "Hour", 60, minute );
var speed = kilometre / hour;
var myDistance = 3.WithUnit( kilometre );
var mySpeed = 6.WithUnit( speed );
var myTime = myDistance / mySpeed;
myTime.ToString( CultureInfo.InvariantCulture ).Should().Be( "0.5 h" );
myTime.CanConvertTo( minute ).Should().BeTrue();
myTime.ConvertTo( minute ).ToString().Should().Be( "30 min" );
myTime.CanConvertTo( second ).Should().BeTrue();
myTime.ConvertTo( second ).ToString().Should().Be( "1800 s" );
}
And for fun (and more test), let’s check this against “poetic units”. The Google unit converter states that:

I choose the US measures because it is defined by inches (the US gallon is defined as 231 cubic inches) and hence is funnier for us than the imperial gallon that is directly related to meters.
An inch is (for sure) 2.54 centimetre. A US mile is now the International Mile that is 1.609344 km. But be careful, there are tons of different miles in US, UK and other countries (see https://en.wikipedia.org/wiki/Mile).
For us, French people (who inspired the modern S.I by the way), this is pure poetry.
public void poetic_units()
{
var metre = MeasureUnit.Metre;
var decimetre = MeasureStandardPrefix.Deci[metre];
var centimetre = MeasureStandardPrefix.Centi[metre];
var kilometre = MeasureStandardPrefix.Kilo[metre];
var hundredKilometre = MeasureStandardPrefix.Hecto[kilometre];
var litre = decimetre ^ 3;
var inch = MeasureUnit.DefineAlias( "in", "Inch", 2.54, centimetre );
var gallon = MeasureUnit.DefineAlias( "gal", "US Gallon", 231, inch ^ 3 );
var mile = MeasureUnit.DefineAlias( "mile", "Mile", 1.609344, kilometre );
var milesPerGalon = mile / gallon;
var litrePerHundredKilometre = litre / hundredKilometre;
var oneMilesPerGallon = 1.WithUnit( milesPerGalon );
oneMilesPerGallon.CanConvertTo( litrePerHundredKilometre ).Should().BeTrue();
var result = oneMilesPerGallon.ConvertTo( litrePerHundredKilometre );
result.Value.Should().BeApproximately( 235.215, 1e-3 );
}
THIS FAILS!
oneMilesPerGallon.CanConvertTo( litrePerHundredKilometre) is false… simply because these two units are inverted:
- Miles/Gallon ≡ distance / distance ^3 ≡ distance^2
- Litre/Kilometre ≡ distance ^ 3 / distance ≡ distance^-2.
We can handle this (and make our library a little bit smarter):
public bool CanConvertTo( MeasureUnit u ) => Unit.Normalization == u.Normalization
|| Unit.Normalization == u.Normalization.Invert();
public Quantity ConvertTo( MeasureUnit u )
{
if( !CanConvertTo( u ) )
{
throw new ArgumentException( $"Can not convert from '{Unit}' to '{u}'." );
}
if( Unit.Normalization == u.Normalization )
{
FullFactor ratio = Unit.NormalizationFactor.DivideBy( u.NormalizationFactor );
return new Quantity( Value * ratio.ToDouble(), u );
}
else
{
FullFactor ratio = Unit.NormalizationFactor.Multiply( u.NormalizationFactor );
return new Quantity( 1/(Value * ratio.ToDouble()), u );
}
}
And this works!
While implementing the first test for quantity, I used (to complicate a little bit the test) the following definition of the hour:
var minute = MeasureUnit.DefineAlias( "min", "Minute", 60, second );
var hour = MeasureUnit.DefineAlias( "h", "Hour", 60, minute );
A test from yesterday uses:
var hour = MeasureUnit.DefineAlias( "h", "Hour", 60 * 60, second );
And tests are now broken: the first to execute registers its definition of the hour, the second redefinition is (rightly) detected as not being the same. The “culprit” is here (internal code):
static AliasMeasureUnit RegisterAlias(string a, string n, FullFactor f, MeasureUnit d)
{
return Register( abbreviation: a,
name: n,
creator: () => new AliasMeasureUnit( a, n, f, d ),
checker: m => m.DefinitionFactor == f && m.Definition == d
);
}
The last parameter is the “checker”: a function that the Register core function calls to check that the actually registered measure is the “same” (so that you cannot define different units of measure with the same abbreviation – abbreviation is the key).
Are the two “hours” defined above the same or not?
Unfortunately, it depends on your business needs. However, it is easy to relax the check here by challenging instead of the exact definition, its normalization:
checker: m => m.Definition.Normalization == d.Normalization
&& m.NormalizationFactor == d.NormalizationFactor.Multiply( f ) );
Should we implement the strict or the relaxed check? Again, it depends on your business needs.
When developing a library that aims to be used in different contexts, my recommendation is to be very cautious about taking such abrupt decisions, I always try to NOT anchor such behaviors/choices deep inside the code (and a difficult part of library development is to identify those choices).
Before tackling this, I’d like to refactor the code. It works well but, up to me, there is a huge issue with current architecture: there is one and only one, global, context for the unit of measures. If you took the time to read this https://en.wikipedia.org/wiki/Gallon or this https://en.wikipedia.org/wiki/Ounce or https://en.wikipedia.org/wiki/Ton-force, can you imagine that an awful singleton will be able to work in a web application that can be used by different customers or manipulates units of measure from different fields?
“Yes… but a singleton is so easy to use!”
Right. The refactoring will preserve the current API: it will be the Default measure context. But you’ll be able to create as many independent MeasureContext as you need (some of them not having the Metre/Gram, etc. default units of measure).
...Refactoring done. The static “easy to use” standard units exposed by the MeasureUnit are now simple relays to the StandardMeasureContext.Default singleton:
public static FundamentalMeasureUnit Unit => StandardMeasureContext.Default.Unit;
Whenever measures are mixed from different contexts, an exception is raised:
[Test]
public void measures_from_different_contexts_must_not_interfere()
{
var kilogram = MeasureUnit.Kilogram;
kilogram.Should().BeSameAs( StandardMeasureContext.Default.Kilogram );
var another = new StandardMeasureContext();
var anotherKilogram = another.Kilogram;
anotherKilogram.Should().NotBeSameAs( kilogram );
another.Invoking( c => c.DefineAlias( "derived", "Derived", 2, kilogram)).Should()
.Throw<Exception>()
.Where( ex => ex.Message.Contains( "Context mismatch" ) );
StandardMeasureContext.Default
.Invoking( c => c.DefineAlias( "derived", "Derived", 2, anotherKilogram ).Should()
.Throw<Exception>()
.Where( ex => ex.Message.Contains( "Context mismatch" ) );
Action a = () => Console.WriteLine( kilogram / anotherKilogram );
a.Should().Throw<Exception>()
.Where( ex => ex.Message.Contains( "Context mismatch" ) );
}
The previous API has not changed but now you can create independent MeasureContext with no unit inside except its “None”, or use the StandardMeasureContext that exposes and already define the Unit, Bit, Byte, and the 7 S.I units.
Enough for today.
I started the day by enhancing the Quantity with operators so that this is now supported:
[Test]
public void Quantity_operators_override()
{
var d1 = 1.WithUnit( MeasureUnit.Metre );
var d2 = 2.WithUnit( MeasureUnit.Metre );
var d3 = d1 + d2;
d3.Value.Should().Be( 3.0 );
var d6 = d3 * 2;
d6.Value.Should().Be( 6.0 );
var s36 = d6 ^ 2;
s36.Value.Should().Be( 36.0 );
s36.Unit.Should().Be( MeasureUnit.Metre * MeasureUnit.Metre );
var sM36 = -s36;
sM36.Value.Should().Be( -36.0 );
sM36.Unit.Should().Be( MeasureUnit.Metre * MeasureUnit.Metre );
(s36 - sM36).Value.Should().Be( 72.0 );
(s36 + sM36).Value.Should().Be( 0.0 );
var s9 = d3 * d3;
s9.Value.Should().Be( 9.0 );
s9.Unit.Should().Be( MeasureUnit.Metre * MeasureUnit.Metre );
var r4 = s36 / s9;
r4.Value.Should().Be( 4 );
r4.Unit.Should().Be( MeasureUnit.None );
var s144 = r4 * s36;
s144.Value.Should().Be( 144.0 );
s144.Unit.Should().Be( MeasureUnit.Metre * MeasureUnit.Metre );
var v27 = d3 ^ 3;
v27.Value.Should().Be( 27.0 );
v27.Unit.Should().Be( MeasureUnit.Metre ^ 3 );
(v27 / s9).Should().Be( d3 );
((v27 / s9) == d3).Should().BeTrue();
((v27 / s9) != d3).Should().BeFalse();
}
And then I had an… issue. Any C#/Java/… developer knows that whenever you define Equals (here implementing the IEquatable<Quantity> interface) on an object, it is expected that you also override the Equals(object) and the GetHashCode() methods.
First, we need to define the equality of quantities:
- They must be convertible to each other units.
- Their values must be the same when converted into one (or the other) units.
Thanks to this, “10 dm” (decimeter) will be equal to “1 m”, “0.1 hm” (hectometer), “0.001 km”, etc.
So far so good, implementing equality implies to convert the other quantity into the unit of this quantity and check the resulting value. Of course, if the other quantity cannot be converted, the two quantities are not equal:
public bool Equals( Quantity other ) => other.CanConvertTo( Unit )
&& other.ConvertTo( Unit ).Value == Value;
And at the object level:
public override bool Equals( object obj ) => obj is Quantity q && Equals( q );
Then comes the GetHashCode… We do not have any “other” here. We must compute a hash code that must match the Equal rule but for any Quantity in “isolation”. The solution is to use the Unit.Normalization and NormalizationFactor as the “target” quantity:
public override int GetHashCode() => ConvertTo( Unit.Normalization ).Value.GetHashCode();
This should work… but actually not. This test is awfully red:
[Test]
public void Quantity_with_alias_and_prefixed_units()
{
var metre = MeasureUnit.Metre;
var decametre = MeasureStandardPrefix.Deca[metre];
var decimetre = MeasureStandardPrefix.Deci[metre];
var dm1 = 1.WithUnit( decimetre );
var dam1 = 1.WithUnit( decametre );
var dm101 = dm1 + dam1;
var dam1Dot01 = dam1 + dm1;
dm101.ToString( CultureInfo.InvariantCulture ).Should().Be( "101 dm" );
dam1Dot01.ToString( CultureInfo.InvariantCulture ).Should().Be( "1.01 dam" );
dm101.Equals( dam1Dot01 ).Should().BeTrue();
dm101.GetHashCode().Should().Be( dam1Dot01.GetHashCode() );
}
What? How? Any idea?
Welcome to the floating point hell!

The two double’s hash codes are slightly different. And so are their actual values:

This happens. But the fun here is that:
- The conversions between the two give exact values (both directions).
- The conversion to their common normalized unit (the metre), when expressed as
strings, are also the same:
dm101.ConvertTo( metre ).ToString().Should().Be( "10.1 m" );
dam1Dot01.ConvertTo( metre ).ToString().Should().Be( "10.1 m" );
The latter is due to the double.ToString() implementation that “cleverly” optimizes its output by rounding/cleaning the value.
For more information about floating point issues, don't hesitate to refer to this excellent paper: https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html.
What are our options here?
- ► Forget the hash code
- And keeping the
Equals
- ► Any dictionary that will use a
Quantity as a key will fail miserably.
- And forgetting also the
Equals
- ► This is weird. One expects a value type named “
Quantity” to support equality.
- ► Keeping the current
Equals implementation and provide a hash code:
- As it is currently implemented.
- ► Any dictionary that will use a
Quantity as a key will fail miserably.
- By returning
0
- ► This is perfectly valid (will not introduce any bug) but using such an object as a key in a dictionary will heavily degrade performances (O(1) to O(n)).
- By calling
Math.Round (https://docs.microsoft.com/en-us/dotnet/api/system.math.round) on the converted result.
- ► What kind of rounding? What precision? I have no idea.
GetHashCode() is a method that must run fast. Conversion alone costs, adding a subsequent rounding may not be a great idea.
- ► Finding another
Equals and GetHashCode
Object equality has to be “coherent”, to follow the “Principle of least astonishment”, not necessarily be “exact” (what does “exact” mean with doubles anyway?).
And the idea is simply to use the string representation of the normalized quantity. Two quantities will be equal if and only if their normalized representations are the same. This NormalizedString is now exposed on the Quantity because it is a very practical and useful property.
I choose to store the string representation to avoid recomputing it each time we need it and it is lazily initialized. The Quantity struct is now a little bit heavier (one double – 8 bytes, and 2 object references – 2 x 4 or 8 bytes), this is the price to pay.
The lazy initialization does not protect concurrent access (with a costly lock or even a Compare-And-Swap - Interlocked instruction): the worst thing that may happen is that we may compute the _normalized field twice.
public string ToNormalizedString()
{
if( _normalized == null )
{
_normalized = ConvertTo( Unit.Normalization ).ToString( CultureInfo.InvariantCulture );
}
return _normalized;
}
public override int GetHashCode() => ToNormalizedString().GetHashCode();
public bool Equals( Quantity other ) => ToNormalizedString() == other.ToNormalizedString();
Equality issue solved. But there are two more things that bother me:
- The default
struct Quantity - new Quantity() - has a 0.0 value and a null Unit. This null quantity Unit is currently not handled and this is a time bomb. - Comparable: should
Quantity be comparable? Unfortunately, yes, as much as being equatable.
The null Unit in the default struct new Quantity() has been handled. Even if this default quantity (0,null) is the only case where a null MeasureUnit may pop, I took this opportunity to handle null unit in the whole API.
A null unit is now logically equivalent to the MeasureUnit.None unit (the dimensionless unit). This special unit is now a unique, contextless unit (a true singleton), shared by all MeasureContext. This has had absolutely no impact on the current code, except that now, using a null unit is accepted:
[Test]
public void handling_null_MeasureUnit_as_None()
{
MeasureUnit theNull = null;
var kiloM1 = theNull / MeasureUnit.Kilogram;
kiloM1.Abbreviation.Should().Be( "kg-1" );
var kiloM1Bis = kiloM1 / theNull;
kiloM1Bis.Should().BeSameAs( kiloM1 );
(theNull * kiloM1).Should().BeSameAs( kiloM1 );
(kiloM1 * theNull * theNull * theNull).Should().BeSameAs( kiloM1 );
var none = theNull / theNull;
none.Should().BeSameAs( MeasureUnit.None );
var none2 = theNull * theNull;
none2.Should().BeSameAs( MeasureUnit.None );
}
And the default new Quantity() has now the exact same behavior as if it was bound to the None unit.
[Test]
public void Quantity_kindly_handle_the_default_quantity_with_null_Unit()
{
var qDef = new Quantity();
qDef.ToNormalizedString().Should().Be( "0" );
qDef.CanConvertTo( MeasureUnit.None ).Should().BeTrue();
var kilo = 1.WithUnit( MeasureUnit.Kilogram );
qDef.CanConvertTo( kilo.Unit ).Should().BeFalse();
qDef.CanAdd( kilo ).Should().BeFalse();
kilo.CanAdd( qDef ).Should().BeFalse();
var zeroKilo = qDef.Multiply( kilo );
zeroKilo.ToNormalizedString().Should().Be( "0 kg" );
(qDef * kilo).ToNormalizedString().Should().Be( "0 kg" );
(kilo * qDef).ToNormalizedString().Should().Be( "0 kg" );
(kilo.Multiply( qDef)).ToNormalizedString().Should().Be( "0 kg" );
(qDef / kilo).ToNormalizedString().Should().Be( "0 kg-1" );
var qDef2 = qDef.ConvertTo( MeasureUnit.None );
qDef2.ToNormalizedString().Should().Be( "0" );
}
This was yesterday, end of the afternoon.
And this morning, I’m a little bit scared by this null handling. To protect ONE case, null units are now transparently accepted as a valid synonym of None… however null is not None!
theNull.Abbreviation,theNull.Name,theNull.Divide(), etc.
will throw null reference exceptions. Unless we use extension methods (that would guard and relay to internal implementations) for each and every aspects, this is just a bug factory…
Rollback!
Keeping only the None unit singleton, we now only protect/guard the Quantity.Unit property:
public MeasureUnit Unit => _unit ?? MeasureUnit.None;
The first handling_null_MeasureUnit_as_None test above has been removed, leaving only the second one.
That being done, let’s now sort quantities. First, we must fix the Quantity equality support to introduce the fact that quantities’ units must belong to the same context:
public override int GetHashCode() => Unit.Normalization.GetHashCode()
^ ToNormalizedString().GetHashCode();
public bool Equals( Quantity other ) => Unit.Context == other.Unit.Context
&& ToNormalizedString() == other.ToNormalizedString();
Then we must decide how two unrelated quantities (that do not share the same normalized unit and hence are not actually comparable) compare to each other. This can’t be realistic, this just need to be determinist and stable:
- Inside the same context, two unrelated quantities will use their respective unit’s normalized abbreviation. Thanks to this, when a set of quantities is sorted, all quantities that are bound to the same dimension will be grouped together.
- Cross contexts, we need a way to order contexts and by now, there is none. We add a
Name to a context. The default context has an empty string name, and all other contexts have to be constructed with a name. Thanks to this, quantities that are bound to units in different contexts can be compared.
Mixing units from different contexts should not actually happen. This notion of context is an optional capacity of this library that are relevant in some scenarios typically involving multi-tenancy and/or persisted data. This library does not include a registry of context names or any other central dictionary: contexts, when used, are useful to isolate units and hence should be used in isolation.
Quantity’s CompareTo and comparison operators are available. By the way, an awful bug has been fixed on Prefixed normalized unit (for the “kg/”g” exception). The last step is to rename the library and its namespace to be “CK.UnitsOfMeasure” and setup a build chain in it.
Parsing units was not a big deal since the underlying grammar has already been settled as a consequence of the naming rules previously adopted.
The implemented parsing uses a regular expression after a removal of all white spaces. The input grammar is not strict and we “normalize” the result:
However, supporting parsing raises one issue that was not obvious before: unit names have to follow some rules to avoid ambiguities.
With the current code base, you can define silly units like “m2”… Obviously, a new unit name (i.e., a fundamental or alias) must not contain digits. The first rule will be more strict than this: a unit’s abbreviation must contain only Letters (Char.IsLetter), Symbols (Char.IsSymbol) or our ‘#’ for the “unit”.
Since we support all the standard SI prefixes (metric and binary) and apply them transparently, as soon as a unit “Sv” for instance is defined, all of its prefixed versions should be de facto (or virtually) defined:
ySv (Yocto, 10-24), zSv (Zepto, 10-21), aSv (Atto, 10-18), fSv (Femto, 10-15), pSv (Pico, 10-12), nSv (Nano, 10-9), µSv (Micro, 10-6), mSv (Milli, 10-3), cSv (Centi, 10-2), dSv (Deci, 10-1), daSv (Deca, 101), hSv (Hecto, 102), kSv (Kilo, 103), MSv (Mega, 106), GSv (Giga, 109), TSv (Tera, 1012), PSv (Peta, 1015), ESv (Exa, 1018), ZSv (Zetta, 1021), YSv (Yotta, 1024), KiSv (Kibi, 210), MiSv (Mebi, 220), GiSv (Gibi, 230), TiSv (Tebi, 240), PiSv (Pebi, 250), EiSv (Exbi, 260), ZiSv (Zebi, 270), YiSv (Yobi, 280)
Note: We don’t make any distinction between units that are traditionally used with metric prefixes (like metre) and the one who use (or also use) binary prefixes like “B”/“Byte”.
The second rule would be that before defining a new unit in a context (thanks to DefineAlias or DefineFundamental):
- Any of its own prefixed versions must not conflict with an existing abbreviation:
foreach( var withPrefix in MeasureStandardPrefix.All.Select( p => p.Abbreviation + a ) )
{
if( _allUnits.ContainsKey( withPrefix ) ) return false;
}
- The new abbreviation must not clash with any existing abbreviation or potentially prefixed ones:
var prefix = MeasureStandardPrefix.FindPrefix( a );
if( prefix != MeasureStandardPrefix.None )
{
return !_allUnits.Values
.Where( u => u is FundamentalMeasureUnit || u is AliasMeasureUnit )
.SelectMany( u => MeasureStandardPrefix.All
.Where( p => p != MeasureStandardPrefix.None )
.Select( p => p.Abbreviation + u.Abbreviation ) )
.Any( exists => exists == a );
}
return true;
This works and actually prevents clashes:
[Test]
public void when_minute_is_defined_inch_can_no_more_exist()
{
var c = new StandardMeasureContext( "Empty" );
var minute = c.DefineAlias( "min", "Minute", new FullFactor( 60 ), c.Second );
c.IsValidNewAbbreviation( "in" ).Should().BeFalse();
}
Do you feel comfortable with this? I’m not.
What we have considered so far is that any standard prefix can always been applied to any unit, however this leads to this behavior: defining “in”/”Inch” prevents to define “min”/”Minute”…
All standard prefixes should not apply to all units. KiloHour or MilliMinute are (usually) stupid units. They can always be explicitly defined as an AliasMeasureUnit if needed but should not be automatically considered.
Today, France got its 2nd stars, but more importantly, we can now control whether standard prefixes apply to a unit and dimensionless units are first-class unit’s world citizens.
public enum AutoStandardPrefix
{
None = 0,
Metric = 1,
Binary = 2,
Both = 3
}
DefineAlias and DefineFundamnetal now accept the enum above (with None default). Thanks to this, minutes and inches can now peacefully coexist:
[Test]
public void minute_and_inch_can_coexist_unless_inch_supports_metric_prefixes()
{
var cM = new StandardMeasureContext( "WithMinute" );
var minute = cM.DefineAlias( "min", "Minute", new FullFactor( 60 ), cM.Second );
cM.IsValidNewAbbreviation( "in", AutoStandardPrefix.None ).Should().BeTrue();
cM.IsValidNewAbbreviation( "in", AutoStandardPrefix.Binary ).Should().BeTrue();
cM.IsValidNewAbbreviation( "in", AutoStandardPrefix.Metric ).Should().BeFalse();
var cI = new StandardMeasureContext( "WithInchMetric" );
var inch = cI.DefineAlias( "in",
"Inch",
2.54,
MeasureStandardPrefix.Centi[cI.Metre],
AutoStandardPrefix.Metric );
cI.IsValidNewAbbreviation( "min", AutoStandardPrefix.None ).Should().BeFalse();
}
When a MeasureStandardPrefix is applied to a unit that doesn’t support the prefix, the adjustment factor handles the exponent.
[Test]
public void prefix_applied_to_non_prefixable_units_use_the_adjusment_factor()
{
var c = new MeasureContext( "NoPrefix" );
var tUnit = c.DefineFundamental( "T", "Thing", AutoStandardPrefix.Binary );
var kiloT = MeasureStandardPrefix.Kilo[tUnit];
var kibiT = MeasureStandardPrefix.Kibi[tUnit];
kiloT.Abbreviation.Should().Be( "(10^3)T" );
kibiT.Abbreviation.Should().Be( "KiT" );
}
We now use PrefixedMeasureUnit internally to define dimensionless units as an alias to the MeasureUnit.None singleton: 10^5.2^6 is now a valid (dimensionless) unit and parsing has been updated to handle such dimensionless units:
[TestCase( "10^-1", "10^-1" )]
[TestCase( "2^7.10^-1*10^3.2^3", "10^2.2^10" )]
[TestCase( "10^-1*2^7.10^3.2^3", "10^2.2^10" )]
[TestCase( "%", "%" )]
[TestCase( "10^2.%", "" )]
[TestCase( "%.10^2", "" )]
[TestCase( "%.‱", "10^-6" )]
public void parsing_dimensionless_units( string text, string rewrite )
{
var ctx = new StandardMeasureContext( "Empty" );
var percent = ctx.DefineAlias( "%", "Percent", new ExpFactor( 0, -2 ), MeasureUnit.None );
var permille = ctx.DefineAlias( "‰", "Permille", new ExpFactor( 0, -3 ), MeasureUnit.None );
var pertenthousand = ctx.DefineAlias( "‱", "Pertenthousand",
new ExpFactor( 0, -4 ), MeasureUnit.None );
ctx.TryParse( text, out var u ).Should().BeTrue();
u.ToString().Should().Be( rewrite );
}
And here it is: percent and other linear (exponential base 10 or 2) factor can now be used just like other units:
[Test]
public void dimensionless_quantity_like_percent_or_permille_works()
{
var percent = MeasureUnit.DefineAlias
( "%", "Percent", new ExpFactor( 0, -2 ), MeasureUnit.None );
var permille = MeasureUnit.DefineAlias
( "‰", "Permille", new ExpFactor( 0, -3 ), MeasureUnit.None );
var pertenthousand = MeasureUnit.DefineAlias
( "‱", "Pertenthousand", new ExpFactor( 0, -4 ), MeasureUnit.None );
var pc10 = 10.WithUnit( percent );
pc10.ToString().Should().Be( "10 %" );
var pm20 = 20.WithUnit( permille );
pm20.ToString().Should().Be( "20 ‰" );
var pt30 = 30.WithUnit( pertenthousand );
pt30.ToString().Should().Be( "30 ‱" );
(pc10 * pm20 * pt30).ToString().Should().Be("6000 10^-9");
(pc10 + pm20 + pt30).ToString( CultureInfo.InvariantCulture ).Should().Be( "12.3 %" );
(pt30 + pc10 + pm20).ToString( CultureInfo.InvariantCulture ).Should().Be( "1230 ‱" );
var km = MeasureStandardPrefix.Kilo[MeasureUnit.Metre];
var km100 = 100.WithUnit( km );
var pc10OfKm100 = pc10 * km100;
pc10OfKm100.ToString().Should().Be( "1000 10^-2.km" );
pc10OfKm100.ConvertTo( km ).ToString().Should().Be( "10 km" );
}
This ends Day 9. The functional surface and the coherency of the whole library justify to release a 0.1.0 version of CK.UnitsOfMeasure.
There is still room for improvements:
The source code under GNU Lesser General Public License v3.0 is available here:
The NuGet package is available from nuget.org:
It has absolutely no dependencies and targets netstandard 2.0.
Safety
"Safety" is a complex concept. I tried in this library to think of all the edge cases that may happen and made choices that I considered the safest possible ones. For instance:
- There is no risk of falling out of the bound of the unit system. If an intermediate computation applies crazy prefixes or combines quantities in a way that lead a unit to be insanely tiny or huge, it is transparently handled by the unit factor.
MeasureContexts isolate groups of units from each other. Any attempt to mix units from different contexts are detected, however some operations such as comparing 2 units or quantities is possible: this is crucial when you need to work with units or quantities regardless of their contexts, typically in infrastructure code (persistence layer for instance).- Naming unicity and prefix handling is a third example of not so trivial stuff (recall the "milli inch" that is abbreviated in "min"). The way the aliases/prefix naming is managed guaranties as much as possible that the unit system will do things correctly as decided by the developer without bad surprise.
Floating Point Hell
Day 6 was fun. If you have skipped it, read it. It's also related to "safety" and in this domain, floating points are not good citizens. The discussion about what equality (and its GetHashCode companion) means, should interest any developer. And I'm curious to have any alternate solution to this issue.
A Singleton... or Not
This library shows a simple way to offer singletons that actually are not. The benefits are obvious: you have the simplicity of the Singleton without any of its caveats except one: as soon as you use the Default instance, your code base is relying on an implicit dependency and you will have to pay the price if your program gets big.
In terms of library, this is perfect since the library does not impose you any architecture. Small project can use the singleton, large projects should instantiate, manage, injects the "no-more-singleton" as any other services.
I have used this pattern a number of times but haven't seen it clearly exposed elsewhere.
Conclusion: The Beauty of Our Job
This project is a very good example of my day-to-day job. Consider a problem, a question ("How should we manage quantities?"), search for existing answers, read about it (it was like going back to school, my physics courses were so long ago), model it in the simplest way you can imagine but with provisions for future expansion, challenge it, refactor, remodel, rechallenge... and enjoy.
Success is a journey, not a destination. The doing is often more important than the outcome. - Arthur Ashe
Updates
2019-05-21
2020-01-21
- NetCore 3 changed the output of Double.ToString()... This is for the best: ToString() method is now "roundtrippable" by default. (Please have a look at this excellent post https://devblogs.microsoft.com/dotnet/floating-point-parsing-and-formatting-improvements-in-net-core-3-0/.)
However, this caused a serious issue to this library since we are using the string representation as an efficient "rounded equality implementation".
To accomodate this change, a new Quantity.ToRoundedString() method explicitly uses the "G15" format when calling Double.ToString(string, IFormatProvider) (with the CultureInfo.InvariantCulture) to obtain a string where small rounding adjustments are erased. This worked perfectly well for our "equality" need. - Thanks to Dave Hary (see questions and answers below), we can now convert dimensionless units into each others.
- Before: even if kg.g-1 was normalized as the dimensionless Measure.None, it was not possible to convert it into Measure.None or other derived dimensionless units (like % or permille).
- Now: Thanks to the removal of one line (see the answer below), we can convert such dimensionless quantity into pure ratio (Measure.None) or % or any other such units.
2020-02-11
- Concerning the implicit conversion/simplification asked by Dave Hary in its first question, this would oblige to implicitly choose a simplified unit but this impacts the multiplication factor.
For example: multiplying "5 kg" by "7 g" gives us "35 g.kg" (units are ordered by descending power and then by lexicographic order). These 2 units share the same normalized unit (the kg): one may simplify them by kg2... However this has an obvious impact on the value itself as the following test shows it.
[Test]
public void automatic_unit_simplification_impacts_the_value()
{
var q = 5.WithUnit( MeasureUnit.Kilogram ) * 7.WithUnit( MeasureUnit.Gram );
q.ToString().Should().Be( "35 g.kg" );
q.Unit.Normalization.Should().Be( MeasureUnit.Kilogram * MeasureUnit.Kilogram );
q.Unit.NormalizationFactor.Should().Be( new ExpFactor( 0, -3 ) );
var qkg = q.ConvertTo( MeasureUnit.Kilogram * MeasureUnit.Kilogram );
qkg.Value.Should().Be( 35.0 / 1000 );
var qg = q.ConvertTo( MeasureUnit.Gram * MeasureUnit.Gram );
qg.Value.Should().Be( 35.0 * 1000 );
}
Question: Should the value be 0.035 (in kg²) or 35000 (in g²)?
Answer: We consider that we should not decide this: it is up to the user/developer to decide to use the "normalized" unit (that is always available) or any variation of it through conversion.
A new version has been released with these changes today: https://www.nuget.org/packages/CK.UnitsOfMeasure/0.2.0.
