Introduction
In this series, I am going to rewrite the Turing machine I wrote in Creating a Turing machine in Python. I am re-writing this to become more familiar with the Rust programming language and to improve my proficiency with it.
You can find the entire project on https://github.com/phillikus/rust_tm.
Let’s first revisit the fundamental theory behind Turing machines and set up the project based on that.
Requirements
- Basic knowledge of the Rust programming language
- Fundamentals of theoretical computer science
What Is a Turing Machine?
A Turing machine is a mathematical model of computation that reads and writes symbols of a tape based on a table rules. Each Turing machine can be defined by a list of states and a list of transitions. Based on a start state (s0), the Turing machine works its way through all the states until it reaches a final state (sf). If no transition leads to the final state, the Turing machine will run ‘forever’ and eventually run into errors.
A transition is defined by the current state, the read symbol at the current position on the tape, the next state and the next symbol that must be written to the tape. Additionally, it contains a direction to determine whether the head of the tape should move the left, right or not at all. To visualize this process, let’s take a look at a very simple Turing machine that increments the value from the initial tape by one.
Unary Increment
To keep it simple, we will start with a unary Turing machine. A one is represented by a ‘|’. So, a Turing machine that contains the number 3 would look like this:
$|||#
The $ represents the starting point of our Turing machine and # represents the end. After the Increment is complete, we expect the final tape to look like this:
$||||#
To reach that final state, our Turing machine simply has to read through all the ‘|’ and append a single ‘|’.
This can be represented by three states s0, s1 and sf with the following transitions:
(s0, ‘$’, s1, ‘$’, Right)
(s1, ‘|’, s1, ‘|’, Right)
(s1, ‘#’, sf, ‘|’, Neutral)
which can also be represented with the following state transition diagram:
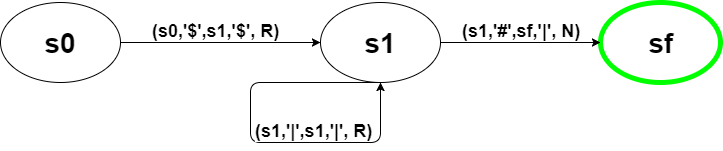
We start in state s0 where we expect to read a ‘$’. Then we switch to state s1 and write back that ‘$’. Then, we move the head one character to the right.
In state s1, as long as we read a ‘|’, we stay in state s1 and write back that ‘|’. This way, we will move all the way to the right end of the tape.
Finally, when we encounter an “#”, we write a ‘|’ and go to the final state sf. Since we are done, there is no reason to move the head at this point.
Project Structure
While this is a very simple Turing machine, we can use the same model to create machines of any complexity. With that knowledge, we are now ready to lay out the basic structure of our project. To represent the entire Turing machine, we will need one struct for the states, the transitions and the tape.
Additionally, we need an enumeration to represent the three directions in which we can move the head of the Turing machine: Left, Right and None (no movement).
Finally, we need one component that combines all these components and uses them to process the Turing machine. To set up the project, open a command line and type:
cargo new rust_tm
This should create a Cargo.toml file as well as a src/ directory with a lib.rs file. Deleting this file and adding a file for each of the structs we will need, I ended up with the following structure:

We are now ready to dive right into the code, so let’s go!
direction.rs
This file contains the enum that will be used to determine in which direction the head of the tape should move. Its implementation is very straightforward:
#[derive(Copy)]
pub enum Direction {
Right,
Left,
None
}
impl Clone for Direction {
fn clone(&self) -> Direction { *self }
}
As you can see, I added an implementation for the Clone trait. You will see later why that is needed.
tape.rs
We will use this enum in the tape struct, defined in tape.rs:
use direction;
pub struct Tape {
pub alphabet: Vec<char>,
pub head_position: i32,
pub tape: Vec<char>
}
As you can see, a tape consists of an alphabet which consists of all valid characters of the Turing Machine, its head position to know where it should read/write the next character and the tape itself, which is just a list of characters.
Since we can’t define methods in the struct itself, we will add those in its implementation:
impl Tape {
pub fn new(alphabet: &str, tape: &str) -> Tape {
Tape { alphabet: alphabet.chars().collect(), head_position: 0, tape: tape.chars().collect() }
}
pub fn write(&mut self, character: char) {
if !(self.head_position >= 1 && self.alphabet.contains(&character)) {
return
}
self.tape[self.head_position as usize] = character;
}
pub fn read(&mut self) -> char {
if self.head_position as usize > self.tape.len() {
panic!("Trying to read character at invalid position: {}.",
self.head_position.to_string());
}
self.tape[self.head_position as usize]
}
pub fn move_head(&mut self, direction: direction::Direction) {
match direction {
direction::Direction::Right => { self.head_position += 1; },
direction::Direction::Left => { self.head_position -= 1; },
direction::Direction::None => {}
}
if self.head_position < 0 {
self.head_position = 0;
}
if self.head_position >= self.tape.len() as i32 {
self.tape.push('#');
}
}
pub fn to_string(&self) -> String {
self.tape.iter().collect()
}
}
Let’s walk through it step by step:
Since Rust itself doesn’t provide any form of constructors, we will initialize the Tape in the new method, which takes a word and an alphabet as parameters. To make calling this method straightforward, both parameters take a &str which is then converted into a Vec<char>.
Additionally, we initialize the head_position to 0, representing the start of the tape.
The write and read methods simply read or write a character from/to the tape. If we try to write at position 0 (the start of the tape), or we try to write an invalid character, the code will simply return to prevent corrupt states.
When we try to read past the length of the tape, our code will panic and display an exception message.
The move_head method takes in a Direction and moves the head of the tape in that direction. Again, I added some bounds checks to prevent the head from exiting the bounds of the tape.
state.rs
This component contains another enum, which represents the type of the state as well as the State struct + implementation themselves:
#[derive(PartialEq)]
#[derive(Copy)]
pub enum StateType {
Start,
Empty,
Final
}
#[derive(Copy)]
pub struct State {
pub id: char,
pub state_type: StateType
}
impl State {
pub fn new(id: char, state_type: StateType) -> State {
State { id, state_type }
}
}
impl Clone for StateType {
fn clone(&self) -> StateType { *self }
}
impl Clone for State {
fn clone(&self) -> State { *self }
}
The struct itself contains only an id and a state-type, which will later be evaluated by the Turing Machine. The only states we will need are: Start, Final and Empty. The Turing machine starts at the Start-state and ends when it reaches the Final state. All Empty states lie in between.
Notice again how I had to implement the Clone trait for both the enum and the class (more on that in a minute).
transition.rs
In the same manner, we can now define the Transition struct which represents the flow from one state of the Turing Machine to the next. It contains the current and next state as well as the current and next char to write to the tape:
use state;
use direction;
#[derive(Copy)]
pub struct Transition {
pub current_state: char,
pub current_char: char,
pub new_state: char,
pub new_char: char,
pub direction: direction::Direction
}
impl Transition {
pub fn new(current_state: char, current_char: char,
new_state: char, new_char: char, direction: direction::Direction) -> Transition {
Transition { current_state, current_char, new_state, new_char, direction }
}
}
impl Clone for Transition {
fn clone(&self) -> Transition { *self }
}
The only method we provide is new to allow us to create new transitions quickly. Beside that, this module doesn’t contain any logic.
tm.rs
With everything set in place, it’s time to take a look at the TM.rs file. This is where all the heavy lifting is done:
use tape;
use direction;
use transition;
use state;
use std;
pub struct TM {
states: Vec<state::State>,
transitions: Vec<transition::Transition>,
pub tape: tape::Tape
}
impl TM {
pub fn new(states: Vec<state::State>, transitions: Vec<transition::Transition>,
tape: tape::Tape) -> TM {
TM { states, transitions, tape }
}
pub fn process(&mut self, verbose: bool) { ... }
}
As you can see, our TM struct consists of a list of states, a list of transitions and a tape. All of them will be used by the process method to produce the final output of the Turing Machine, so let’s take a closer look into that:
pub fn process(&mut self) {
let mut current_state: state::State = self.get_first_state();
let mut step: i32 = 0;
self.log_step(step);
while current_state.state_type != state::StateType::Final {
let current_char = self.tape.read();
let state_id = current_state.id;
let transition = *self.transitions.iter().clone()
.find(|transition| transition.current_state == state_id &&
transition.current_char == current_char).unwrap();
current_state = *self.states.iter().clone().find(|state|
state.id == transition.new_state).unwrap();
step += 1;
self.tape.write(transition.new_char);
self.tape.move_head(transition.direction);
self.log_step(step);
}
}
First, we initialize a current_state variable and set it to the start state of the Turing Machine. To get this first state, I created the following helper method:
fn get_first_state(&self) -> state::State {
let mut iter = self.states.iter().cloned();
let first_state: Option<state::State> =
iter.find(|state| state.state_type == state::StateType::Start);
match first_state {
None => panic!("No start state found."),
Some(state) => state
}
}
First, we get a mutable iterator and clone it so we can use it without running into borrowing errors. This is also why we had to implement the Clone trait earlier. Then we try to find the first state where the state_type == Start.
If we found a state, it will be returned, otherwise, our code will panic and crash again.
Back in our process method, we initialize a step variable to count the number of steps our Turing machine has taken so far. Then, we log this number as well as the current tape with the log_step method:
fn log_step(&mut self, step: i32) {
println!("Tape after step {0}: {1} -> Head position: {2}", step,
self.tape.to_string(), self.tape.head_position);
}
Here, we simply print the tape and its head position in a nicely formatted matter.
All the magic, however, happens inside the while loop of the process method:
while current_state.state_type != state::StateType::Final {
let current_char = self.tape.read();
let state_id = current_state.id;
let transition = *self.transitions.iter().clone()
.find(|transition| transition.current_state == state_id &&
transition.current_char == current_char).unwrap();
current_state = *self.states.iter().clone().find
(|state| state.id == transition.new_state).unwrap();
step += 1;
self.tape.write(transition.new_char);
self.tape.move_head(transition.direction);
self.log_step(step);
}
Based on current_char and state_id, we try to find the first matching transition.
Once we have a transition, we will try to find the next state based on the state of that transition. Once this is done, we simply increment the number of steps our Turing Machine has run through, write the new character to the tape and move the head in the according direction.
We also write call our log_step to print the result of the previous step to the console.
This is all we have to do to push the Turing machine to the next state. This step will be repeated until the Turing machine reaches the Final state.
Testing the Turing Machine
Let’s go ahead and visualize this process by testing our machine. To keep it simple, let’s start with the Increment Turing machine I showed you in the beginning. To create such a machine, simply initialize and run it from main.rs:
mod state;
mod tape;
mod direction;
mod transition;
mod tm;
fn main() {
let mut tm : tm::TM = increment("$||#");
tm.process(true);
}
fn increment(word: &str) -> tm::TM {
let mut tape = tape::Tape::new("$|#", word);
let states = vec![
state::State::new('0', state::StateType::Start),
state::State::new('1', state::StateType::Empty),
state::State::new('f', state::StateType::Final)
];
let transitions = vec![
transition::Transition::new('0', '$', '1', '$', direction::Direction::Right),
transition::Transition::new('1', '|', '1', '|', direction::Direction::Right),
transition::Transition::new('1', '#', 'f', '|', direction::Direction::None)
];
tm::TM::new(states, transitions, tape)
}
I initialized the tape with the value ‘||’ and added ‘|’ as only valid character (beside $ and #). Then, I defined the states and transitions and used them to instantiate the TuringMachine. Calling its process method should then go through all these states and transitions and write a final ‘|’ at the end of the tape.
If we have done everything correctly thus far, we should see the following output on our console:
philipp@psrv1 ~/P/r/rust_tm> cargo run
Finished dev [unoptimized + debuginfo] target(s) in 0.0 secs
Running `target/debug/rust_tm`
Tape after step 0: $||
Tape after step 1: $||
Tape after step 2: $||
Tape after step 3: $||
Tape after step 4: $||| -> Head position: 3
Advanced Turing Machines
Now that our Turing machine is up and running, it’s time to add some more interesting machines. We will stick with unary Turing machines and implement one for Decrement, Addition and Subtraction each:
Decrement Machine
The Decrement Machine works very similar to the Increment Machine. However, instead of adding a |, we have to remove the last one after we reach the end of the tape. This means we have to move to the right until we reach the first # character. Then we can simply go one character to the left and remove that |:

In Rust, we can represent this Turing machine with the following code:
...
fn main() {
let mut tm : tm::TM = decrement("$|||#");
tm.process(true);
}
fn decrement(word: &str) -> tm::TM {
let tape = tape::Tape::new("$|#", word);
let states = vec![
state::State::new('0', state::StateType::Start),
state::State::new('1', state::StateType::Empty),
state::State::new('2', state::StateType::Empty),
state::State::new('f', state::StateType::Final)
];
let transitions = vec![
transition::Transition::new('0', '$', '1', '$', direction::Direction::Right),
transition::Transition::new('1', '|', '1', '|', direction::Direction::Right),
transition::Transition::new('1', '#', '2', '#', direction::Direction::Left),
transition::Transition::new('2', '$', 'f', '$', direction::Direction::None),
transition::Transition::new('2', '|', 'f', '#', direction::Direction::None)
];
tm::TM::new(states, transitions, tape)
}
Running the code now will yield the following result instead:
cargo run
Finished dev [unoptimized + debuginfo] target(s) in 0.0 secs
Running `target/debug/rust_tm`
Tape after step 0: $|||
Tape after step 1: $|||
Tape after step 2: $|||
Tape after step 3: $|||
Tape after step 4: $|||
Tape after step 5: $|||
Tape after step 6: $||
Addition Machine
Another simple Turing machine we can create is one that adds two numbers. We will represent the addition operation by two unary numbers separated by an &. For example, to calculate the sum of the numbers two and three, we would initialize the tape like this: $||%|||.
To add these numbers, all we have to do is to replace the & with a | and then remove the last |. For the tape above, this would result in $|||||. To realize this, the Turing machine has to go to the right until it reaches the %, replace it with | and then move further to the right until it reaches the end of the tape, marked by a #. Finally, it has to go one character to the left and remove the final |:

This translates into the following Rust code:
...
fn main() {
let mut tm : tm::TM = add("$|||#");
tm.process(true);
}
fn add(word: &str) -> tm::TM {
let tape = tape::Tape::new("$|&#", word);
let states = vec![
state::State::new('0', state::StateType::Start),
state::State::new('1', state::StateType::Empty),
state::State::new('2', state::StateType::Empty),
state::State::new('3', state::StateType::Empty),
state::State::new('4', state::StateType::Empty),
state::State::new('f', state::StateType::Final)
];
let transitions = vec![
transition::Transition::new('0', '$', '1', '$', direction::Direction::Right),
transition::Transition::new('1', '#', 'f', '#', direction::Direction::None),
transition::Transition::new('1', '|', '1', '|', direction::Direction::Right),
transition::Transition::new('1', '&', '2', '|', direction::Direction::Right),
transition::Transition::new('2', '|', '2', '|', direction::Direction::Right),
transition::Transition::new('2', '#', '3', '#', direction::Direction::Left),
transition::Transition::new('3', '|', '4', '#', direction::Direction::Left),
transition::Transition::new('4', '|', '4', '|', direction::Direction::Left),
transition::Transition::new('4', '$', 'f', '$', direction::Direction::None)
];
tm::TM::new(states, transitions, tape)
}
Running the machine will yield the following result:
cargo run
Finished dev [unoptimized + debuginfo] target(s) in 0.0 secs
Running `target/debug/rust_tm`
Tape after step 0: $|||&||
Tape after step 1: $|||&||
Tape after step 2: $|||&||
Tape after step 3: $|||&||
Tape after step 4: $|||&||
Tape after step 5: $||||||
Tape after step 6: $||||||
Tape after step 7: $||||||
Tape after step 8: $||||||
Tape after step 9: $|||||
Tape after step 10: $|||||
Tape after step 11: $|||||
Tape after step 12: $|||||
Tape after step 13: $|||||
Tape after step 14: $|||||
Tape after step 15: $|||||
Subtraction Machine
So far, our Turing machines have been fairly trivial. Now let’s tackle a more complicated problem: Subtraction. One way to solve this problem is to move through the tape until we reach the first # (which we will use as Minus operator). Then we have to remove the next | on its right and left side and replace them with #.
For example, given the tape $|||#||#, after these first steps, the tape would look like this: $||###|#. If we repeat this process until there are no more | on the right side of the initial #, the subtraction will be complete. In the case above, we will end up with a tape like: $|#####.
This process will work for tapes of any length. However, since we have to move through an increasing number of # with every step, the Turing machine will take a very long time for large inputs.
As you can see in the image below, the diagram for this Turing machine is much more complicated than the previous ones and it takes some time to fully understand it.

In Rust, this is represented by the following code:
fn main() {
let mut tm : tm::TM = subtract("$|||#||");
tm.process(true);
}
fn subtract(word: &str) -> tm::TM {
let tape = tape::Tape::new("$|#", word);
let states = vec![
state::State::new('0', state::StateType::Start),
state::State::new('1', state::StateType::Empty),
state::State::new('2', state::StateType::Empty),
state::State::new('3', state::StateType::Empty),
state::State::new('4', state::StateType::Empty),
state::State::new('5', state::StateType::Empty),
state::State::new('6', state::StateType::Empty),
state::State::new('7', state::StateType::Empty),
state::State::new('8', state::StateType::Empty),
state::State::new('f', state::StateType::Final)
];
let transitions = vec![
transition::Transition::new('0', '$', '0', '$', direction::Direction::Right),
transition::Transition::new('0', '#', 'f', '#', direction::Direction::None),
transition::Transition::new('0', '|', '1', '|', direction::Direction::Right),
transition::Transition::new('1', '|', '1', '|', direction::Direction::Right),
transition::Transition::new('1', '#', '2', '#', direction::Direction::Right),
transition::Transition::new('2', '#', '2', '#', direction::Direction::Right),
transition::Transition::new('2', '|', '3', '|', direction::Direction::Right),
transition::Transition::new('3', '|', '4', '|', direction::Direction::Left),
transition::Transition::new('3', '#', '6', '#', direction::Direction::Left),
transition::Transition::new('4', '|', '5', '#', direction::Direction::Left),
transition::Transition::new('5', '#', '5', '#', direction::Direction::Left),
transition::Transition::new('5', '|', '2', '#', direction::Direction::Right),
transition::Transition::new('5', '$', '2', '$', direction::Direction::Right),
transition::Transition::new('6', '|', '7', '#', direction::Direction::Left),
transition::Transition::new('7', '#', '7', '#', direction::Direction::Left),
transition::Transition::new('7', '$', 'f', '$', direction::Direction::None),
transition::Transition::new('7', '|', '8', '#', direction::Direction::Left),
transition::Transition::new('8', '|', '8', '|', direction::Direction::Left),
transition::Transition::new('8', '$', 'f', '$', direction::Direction::None)
];
tm::TM::new(states, transitions, tape)
}
Again, running our code yields correct results:
cargo run
Finished dev [unoptimized + debuginfo] target(s) in 0.0 secs
Running `target/debug/rust_tm`
Tape after step 0: $|||
Tape after step 1: $|||
Tape after step 2: $|||
Tape after step 3: $|||
Tape after step 4: $|||
Tape after step 5: $|||
Tape after step 6: $|||
Tape after step 7: $|||
Tape after step 8: $|||
Tape after step 9: $|||
Tape after step 10: $||
Tape after step 11: $||
Tape after step 12: $||
Tape after step 13: $||
Tape after step 14: $||
Tape after step 15: $||
Tape after step 16: $||
Tape after step 17: $||
Tape after step 18: $||
Tape after step 19: $|
Tape after step 20: $|
Tape after step 21: $|
This concludes our collection of Turing machines. I encourage you to play around with them and create new ones. For example, you can try to implement Turing machines for Multiplication and Division.
I hope you enjoyed this article. If you have any questions, problems or feedback, please let me know in the comments.
