Introduction
This assignment demonstrates the basics of scripting using RenderMan scene description (rib) protocol. Addressed are the fundamentals of xyz coordinate system through the creation of basic geometry that is transformed in 3D space. The preliminary renders have been done using basic shading so that the geometry can be more easily seen.
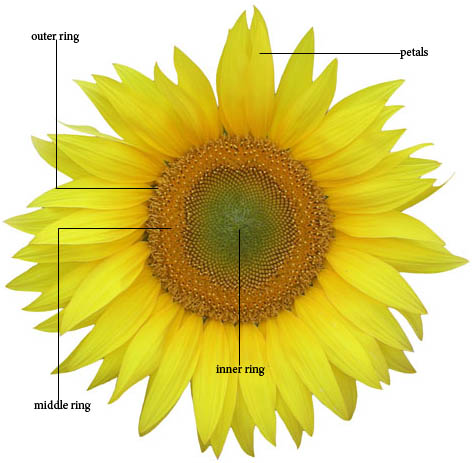
Figure 1
Figure 1 is the sample picture which I took as a reference for the assignment and tried to match the picture in RenderMan. In order to do this assignment, I used the following languages and tools:
- Cutter (a handy text editor for use with various scripting languages and is tightly integrated with a lot of
RenderMan compliant renderers (e.g., PRMan, 3Delight, etc.) as well as modeling packages such as Maya, etc. The author Malcom Kesson, an awesome guy from SCAD is the author of this tool and he’s the one behind the format of these assignments that I’m following as well. Here is his link: www.fundza.com & http://www.sfdm.scad.edu/faculty/mkesson/. - Python (an extremely powerful language that is fast becoming the preferred scripting language for most of the CG applications for its neatness, portability and higher-level functionalities). Download it from here: http://www.python.org/
- 3Delight (an amazing
RenderMan compliant renderer that is the best you can get for playing around with RenderMan for no cost at all!). Get it from here: http://www.3delight.com/en/
For this assignment, I divided my task in different phases. Following are the phases and their details with code snippets.
Step 1 - Internal Pattern of Sunflower
Upon close inspection of the sunflower as seen in the reference image (there are many variants of a sunflower so I just stuck to the one in the reference image), one can see that this sunflower exhibits a very peculiar pattern in the way seeds are arranged internally. Google provided me with more information immediately.

Matlab sample
So, the first task was to determine the internal pattern of a Sunflower which follows the specific pattern shown in the matlab sample, downloaded from Wikipedia entry for a sunflower. It uses the following mathematical formula to form this shape:
// n=1:500;
// r=sqrt(n);
// t=137.5*pi/180*n;
// plot(r.*cos(t),r.*sin(t),'o')
Using cutter to prototype the ribs and then using Python in order to run a loop, I used the Cone primitive (instead of plotting an ‘o’ in the matlab sample code above) to make this seed pattern of the sunflower. Following is the code snippet and rendered view:
// While(n < div):
// p=0.1
// r=0.25*sqrt(n)
// a=137.5*pi/180*n
// X=r*cos(a)
// Y=r*sin(a)
// Z=6-(N/div)*6
// Riattributebegin()
// Riscale(a/div,a/div,a/div)
// Ritranslate(x,y,z)
// RiColor((0.63921568627450980392156862745098,
// 0.50980392156862745098039215686275,
// 0.13725490196078431372549019607843))
// RiCone(0.2,0.2,360)
// Riattributeend()
// n=n+1
| 
|
The matlab code above would only draw a seed pattern in 2D (XY plane) but in reality, the seeds are arranged on a sphere and not plane. One could use the true spherical coordinates in order to find the distribution of cones on top of a sphere but instead, I cheated and simply used a linear interpolation between the radius of the imaginary sphere on which the cones were to distributed and the origin of this sphere (in this case, its zero). The interpolation factor was the gradually increasing radius used in the loop above. This way, while the matlab sample code kept increasing the radius by calculating it as a square root of the loop iterator, I kept decreasing the z value of the seed coordinates all the way down to zero in order to give a ‘bumped’ form where seeds are closer to the camera in the center and gradually push back in the depth as they move towards the boundary. After calculating the appropriate values of x, y and z coordinates, a scaling factor was calculated using linear interpolation as well in order to give the effect of cones (seeds) scaling up as they move towards the boundary. Finally, all these values were applied using appropriate translate and scale commands of rib before drawing the cone primitive.
Step 2 - Randomize Cone based Circle
Next up was the middle ring of seeds. I had to make the cones arrange in a circular ring of a certain width which has cones (seeds) more in dense format and have random positions not exactly following any strict pattern. For this, I used the randomize function of python to get random values, add them to the polar coordinates I calculate using the sin/cos functions and draw the cones on an xy plane in the rib file, using Python.
Add a table with relevant code and images.

Figure 4

Figure 5
Figure 4 is the arrangement of cones in randomize format while in figure 5, you can see the combination of figure 3 and figure 4. To make the randomized pattern of cones, I first take the maximum radius value when I got out of the loop while drawing the inner seed pattern, run a loop up to the radius of the middle ring and by using the random function of python and after some manipulation, get the value of my desired range and then translate the cones and draw them to make the ring.
Step 3 - Randomize Curves on the Circle
If you give a closer look to the inner side of sunflower, you can see it has some hairs type of things which are random in size and also arrange in randomize nature to make this effect I used Curves. In figure 6, you can see the sample of curves by using which I made the third ring of sunflower which is randomized in size and position. Figure 7 is the combination of figure 5 and 6. To make the outermost circle on figure 5, I first take the maximum radius value of figure 5 and after adding some value, define another radius for my curve based circle to make the curves I need the arguments in an array my task Figure 7 Figure 6 was not to make the curves but I have to make it random in size and positions to achieve this task, I first made the function of randomizing between the value required to me and made the array on run time so each curves drawn randomly and change with each other. You can see the function by name of rf() in the source code of the assignment.

Figure 6
Step 4 - Petals of Sunflower
In this step, I have to make the petals for sunflower, initially I made the petals using subdivision surfaces of Renderman and rotate the petals to give the effect of petals and resizing the petals using scaling I made three different layers of petals and each layer is indented towards Z axis along with some rotation to give the look of randomize petals, but later I made three different petals in MAYA and then use these Figure 9 Figure 8 petals using Read Archive for sunflower. Initially for petals, I made the petals in Renderman by using Subdivision Surface and rotate the petals on figure 7 to give the look of random arrangement of petals I scaled the petals and their colors. To give the look of layered petals, I translate the each circle of petal layers in positive Z axis after it I made the three different petals in MAYA and apply them instead of petals which I made in Renderman by using Subdivision surfaces. Selecting criteria of petal is determined on runtime by using the function name randomizebound(a,b). I made this function to get the value according to my desired range, you can see this function in the source code which I made using python. This function took two arguments, first is lower range and the second Is higher range and return the value in between the range excluding the boundaries.

Figure 7

Figure 8
Below is the code in Python:
from math import sin, cos, pi ,sqrt,tan
from cgkit.ri import *
import random
import os
a = 0.0
r = 2.0
n = 0.0
div=500
numdiv=100
def rf():
v=-2+random.random()*4
return v
def subdivmes():
RiScale(0.10,0.10,0.10)
RiSubdivisionMesh("catmull-clark",[8],[0,1,2,3,4,5,6,7],
["interpolateboundary"],[0,0],[],[],"P",
[0, 1, -1, -1, 2, -1, -1, 4, -1, -1, 6, -1, 0, 10, -1, 1, 6, -1, 1, 4, -1, 1, 2, -1])
def petal():
size=randomizebound(32,40)
RiScale(size,size,0)
RiColor((0.85882352941176470588235294117647,
0.85882352941176470588235294117647,0.14509803921568627450980392156863))
def petal1():
size=randomizebound(32,40)
RiScale(size,size,0)
RiColor((0.92549019607843137254901960784314,
0.90588235294117647058823529411765,0.16078431372549019607843137254902))
def petal2():
size=randomizebound(8,10)
RiScale(size,size,0)
RiColor((0.89411764705882352941176470588235,
0.77254901960784313725490196078431,0.14509803921568627450980392156863))
def scale():
size=(random.random()*10)/2
return size
def randomizebound(lowerbound, uperbound):
return lowerbound+(random.random())*(uperbound-lowerbound)
RiBegin("D:\\PythonExample\\sampleflower.rib")
RiDisplay("circle.tiff", "framebuffer", "rgb")
RiProjection("perspective", "fov", 110)
RiTranslate(0, 0, 50)
RiWorldBegin()
y=2
while(n < div):
p=0.1
r=0.25*sqrt(n)
a=137.5*pi/180*n
x=r*cos(a)
y=r*sin(a)
z=6-(n/div)*6
RiAttributeBegin()
RiScale(a/div,a/div,a/div)
RiTranslate(x,y,z)
RiColor((0.63921568627450980392156862745098,
0.50980392156862745098039215686275,0.13725490196078431372549019607843))
RiCone(0.2,0.2,360)
RiAttributeEnd()
n=n+1
rstart=0.25*sqrt(div)+1
i=0.0
while(i<10):
r=rstart+((i/10)*2)
n=0.0
a=0.0
while(n<20):
a=(n/20*360.0)*pi/180.0
x=r*cos(a)
y=r*sin(a)
RiAttributeBegin()
RiScale(2,2,2)
xrand=-0.75+(random.random()*2)
yrand=-0.75+(random.random()*2)
RiTranslate(x+xrand, y+yrand, 0)
RiColor((0.68235294117647058823529411764706,
0.48235294117647058823529411764706,0.15686274509803921568627450980392))
RiCone(0.2,0.2,360)
RiAttributeEnd()
n=n+1
i=i+1
n=0.0
r=r+11
while(n < div):
a=(n/div*360.0)*pi/180.0
x=r*cos(a)
y=r*sin(a)
RiAttributeBegin()
RiTranslate(x+rf(),y+rf(),0)
matrix = [[-6, 0 ,0],
[-3, rf(),0],
[0, rf(),0],
[3, rf(),0],
[6, rf(),0]]
RiAttributeBegin()
RiScale(0.20,0.20,0)
RiColor((0.75686274509803921568627450980392,0.51764705882352941176470588235294,
0.15294117647058823529411764705882))
RiRotate(n/div*360,0,0,1)
RiBasis("bezier", 3, "bezier", 3)
RiCurves("cubic", [5], "nonperiodic", "P", matrix, "constantwidth",0.8)
RiAttributeEnd()
RiAttributeEnd()
n=n+1
n=0.0
r=r
numdiv=20
while(n < numdiv):
a=(n/numdiv*360.0)*pi/180.0
x=r*cos(a)
y=r*sin(a)
RiAttributeBegin()
angle=(n/numdiv)*360.0
RiTranslate(x,y,-1.5)
RiRotate(angle,0,0,1)
0.14509803921568627450980392156863))
RiRotate(10,1,0,0)
subdivmes()
RiAttributeEnd()
n=n+1
n=0.0
r=r
print numdiv
while(n < numdiv):
a=(n/numdiv*360.0)*pi/180.0
x=r*cos(a)
y=r*sin(a)
size=randomizebound(32,40)
RiAttributeBegin()
angle=(n/numdiv)*360.0
0.16078431372549019607843137254902))
RiTranslate(x,y+rf()*2,-1)
RiRotate(angle,0,0,1)
RiRotate(10,0,0,1)
RiScale(size,size,0)
RiRotate(12,1,0,0)
RiAttributeEnd()
n=n+1
n=0.0
r=r
print numdiv
while(n < numdiv):
a=(n/numdiv*360.0)*pi/180.0
x=r*cos(a)
y=r*sin(a)
number=randomizebound(0,3)
print number
RiAttributeBegin()
angle=(n/numdiv)*360.0
0.14509803921568627450980392156863))
RiTranslate(x,y+rf()*2,-0.5)
RiRotate(angle,0,0,1)
RiRotate(15,1,0,0)
if(number>0) and (number <1):
petal()
subdivmes()
if(number>1) and (number <2):
petal()
subdivmes()
if (number >2) and (number <3):
petal2()
subdivmes()
RiAttributeEnd()
n=n+1
RiWorldEnd()
RiEnd()
os.system("renderdl D:/PythonExample/sampleflower.rib")
