Multiple Precision Arithmetic: Division Algorithm

This article is part of a series of articles:

Multiple Precision Arithmetic: A recreational project

• Part #1, The Sum
• Part #2, The Subtraction
• Part #3, The Multiplication
• Part #4, The Division
• Part #5, Using the Code
• Github Repo

Integer Long Division

In this chapter, we'll focus on long division, the most difficult arithmetic operation to implement.

Let's recall the definition of division in ℕ: divide A by B means find the numbers Q and R such that A = B * Q + R, having (R < B) and (A, B, Q, R ∊ ℕ); human readable definition: the division A / B is an operation which divides A items into B groups each having Q elements, when after grouping elements, some element remain which are not enough to be distributed one on each group, those items are called remainder, R for friends.

Example: We have some playing cards, we have some players, we distribute 1 card to each player starting from our left, proceeding clockwise until we don't have enough cards to complete a new round, the amount of cards left is the remainder R, the number of cards each player has at the end is the quotient Q.

To speed up the process to know Q without having to distribute things, we will use a positional number system and an algorithm, let's start.

Build a Primitive Operation "Simple Division"

First, we need a primitive operation that is easy enough to be computed, let define "Simple Division":

Simple Division: The operation A / B , where A and B are such that ...

1. A >= B
2. B has exactly one non-zero digit and A has one or two digits, but when A has two digits, then its leftmost is less than B and non zero

... is a simple division.

Example: 4/3, 37/8, 9/8 are simple divisions on base 10.

Example: 47/3, 3/8, 97/8 are not simple divisions on base 10.

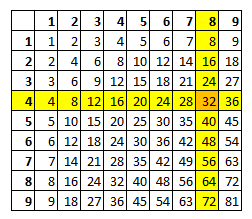
Q and R can be found by inverse lookup on multiplicative b-base Pythagorean table.

Example of inverse lookup on Pythagorean table base 10: Let's compute the simple division 37/8, search, on column 8 of the Pythagorean table, the maximum value that is less than 37, which is 32, the corresponding row index is 4, so 37/8=4, the remainder is 37-32=5

Long Integer Division

In primary school, kids learn a useful algorithm to calculate the long division, that algorithm leverages the representation in base 10 and the knowledge of its multiplicative Pythagorean table, to simplify the work needed to divide larger numbers.

We will use the same algorithm but we will be a little bit pedantic about details because a CPU is not as smart as a 8 y/o child.

Corner Cases

Since this article is about integer division, there are some trivial solutions:

• when B = 0 the result is not defined, it's an error.
• when A < B then A / B=0 and the remainder R =A
• when A equals B then Q = 1 and R = 0
• when A = 0 then Q = 0 and remainder R = 0

Long Integer Division on Digital Computers

Most n-bit CPUs can divide 2n-bit number by a n-bit one, _{when the higher order word of the 2n-bit number is less than the divisor, otherwise it will set some hardware error flag, that is exactly what we need as per the simple definition above}.

We can use hardware division in substitution of pythagorean table lookup then, as our "simple division" on which we'll build the long division algorithm for our computers.

As we did on previous chapters, we need to get the analogy between the base 10 (which 8 Y/o childs use) to the base register_size which the CPU understands: we can imagine a CPU register as a digit, and the built-in division instruction as the Pythagorean table inverse lookup; the same algorithm we learned at school can be applied to CPU then, with some minor variant.

Recap: We can use the elementary school algorithm with digital computers, using the CPU integrated division instruction to lookup the base 2^{register_size} Pythagorean table: some algorithm you find on the web uses base 2 (which is good for implementing it on hardware), but we'll avoid that, to efficiently use existing hardware.

The Algorithm

The idea is to split the division into a sequence of smaller divisions, having the form A_i = B * Q_i + R_i, where Q_i is a single digit number, the purpose of using smaller divisions is to minimize time spent guessing the correct Q.

The flow chart will set the basic idea. For simplicity, the first version of the algorithm requires input A > B, and also, the guessing algorithm is not yet set.

The flowchart was created using the following pseudo code and an online tool, don't be fooled by its apparent single loop structure which may lead you to think to linear complexity, each subtraction, multiplication and comparison are working on multiple digit long numbers, temp numbers are strings of digits too and they could need to be reallocated each time, we'll see when we look at the C code.

/inputs are:  string A, string B/;
string  Q = 0;
string  R = 0;
string  Ai = get as many digits from A, starting from most significant, until Ai >= B;

loop:
  /*step 1 is the obscure part */
   1) int Qi = find the greatest Qi that satisfies : (Qi * B) <= Ai;
   2) Append Qi to Q;  
   3) temp = long_multiply(Qi, B);
   4) Ai = long_subtract(Ai, temp);
   if(have more digits on A?)
   {
     Append(Ai, next digit from A);
     goto loop;
   }

R = Ai;
return outputs are: Q and R;

Now let’s follow the algorithm step by step with an example (for those with enough patience, others can skip):

Suppose we have 2 numbers A=1234 and B=56, and we want to find the result Q (that is 22) and the remainder R (that is 2).

NOTE: In the below pseudocode, the comments precede the commented row

/A = "1234", B = "56" /; 
Q="", R="";

//Ai will be "123", cause A="1234" and B = "56"
Ai = get as many digits from A, starting from most significant, until Ai >= B;

FIRST ITERATION:
loop:
   //Qi become 2, because 2 is the greatest X such that X * 56 <= 123
   1) int Qi = find the greatest Qi that satisfies : (Qi * B) <= Ai;

   // append Qi to the left of Q, so Q will be "2"
   2) Append Qi to Q; 
   
   // temp = "112"
   3) temp = long_multiply(2, "56");

   // Ai = "11"
   4) Ai = long_subtract("123", "112");

   // yes we have one more digit, A was "1234", "123" already used, we still have "4"
   if(have more digits on A?) 
   {
      //Ai = "114", because Ai was "11" and now we append to it "4"
      Append(Ai, next digit from A); 
      goto loop; 
   }

SECOND ITERATION:

loop:

   //Qi become 2, because "2" * "56" = "112", so "2" is 
   //  the greatest X such that X * "56" <= Ai (Ai value is "114") 
   1) int Qi = find the greatest Qi that satisfies : (Qi * "56") <= Ai;

   // append Qi to the left of Q, so Q will be "22" 
   2) Append Qi to Q; 

   // temp = "112"
   3) temp = long_multiply(2, "56");

   // Ai = "114"-"112" = "2"
   4) Ai = long_subtract("114", "112");

   // we run out of digits so we quit loop 
   if(have more digits on A?) 
   { 
      ...
   }

// R="2"  
R = Ai; 
return outputs are: "22" and "2";

How to Find the Correct Q_I

The obscure part in the above algorithm is the first line on the loop: guessing Q_i.

At step 1, we found Q₁, which is always one digit long (good to know), we start by guessing a good candidate, then we will adjust if the guess is wrong: in base 10, there are only 9 candidates (that's why an elementary school teacher does not dig too much into guessing algorithms), on base 2²⁵⁶, that might be a problem.

My Algebra Book Says that the Best First Candidate Q_I is Found This Way

Well, my algebra book does not put things this way but this is derived from the book.

A little note before to start...

... we will not run guess algorithm on the arbitrarily sized A and B, we are within the loop (see above algorithm), let's say we are at step i, thus we are guessing the divisor for the division A_i / B, as you may note the algorithm ensures that A_i is greater than B but not too much, it can have at most 1 digit more than B, but keep in mind that, after the first iteration, A_i could be smaller than B too (on this case, our guess will be 0).

Last note before we start...: following examples use base 10.

How to Guess

• Let B_m be the leftmost digit of B
• Let A_n be the leftmost digit of A_i
• Let A_guess to be the minimum group of (1 or 2) digits of A_i (starting from most significant) such that A_guess >= B_m
  • Example A_i=123, B=56, so B_m is 5, leftmost of A_i is 1, 1 is less than 5, then we must pick another digit from A_i, so A_guess=12.
  • Example A_i=123, B=11, so B_m is 1, leftmost of A_i is 1, since 1 is equals to 1 then A_guess=1.
  • Example A_i=3, B=45, so B_m is 4, leftmost of A_i is 3, but A_i less than B, so A_guess= 0.

Standard Guess

We find our guess Q_i this way:

• Corner case A_{i <} B
  • Q_i = 0
• else if A_n = B_m , then
  • if A_i has same number of digits of B then Q_i = 1
    • example: A_i = 213 : B = 200, Q_i = 1
    • example: A_i = 2137 : B = 2122, Q_i = 1
    • _{the case where Ai < B was already handled by previous branch...}
  • else (_{when Ai is 1 digit longer than B}, _{there are no other possible cases}) Q_i = base-1 (9 for decimal strings, 0xFFFF....F on the CPU).
    • example: A_i = 2137 : B = 220, Q_i = 9
    • _{the case Ai = 2237 : B = 220 cannot exist because: Ai is the shortest leftmost group of digits of A > B, in this case Ai would be 223 thus the case should have been handled by the above branch}
• else
  • Q_i = simple_division(A_guess / B_m), _{where the simple division could be the inverse lookup if we work by hand or the CPU Div instruction on computer.}

Note that A_guess can only be 1 or 2 digits and that when it's 2 digits, then A_n < B_m: so our standard guess of Q_i = A_guess / B_m can be computed using a built-in CPU instruction.

Improved guess: Later on, we'll use some preprocessing: we will get rid of some branching, because we'll preprocess A and B to make B_m >= base/2

How Far from the Real Q_I?

Now we need to ensure we guessed the correct Q_i : to do so, we have to run the long multiplication algorithm B * Q_i , for example 56 * 2 = 112, being 112 <= 123 we are done.

Wait: Should we not check whether our guess is too small? Why don’t we check 56 * 3 < 123 ? Well, that is not possible, our guess will always be correct or too big, never too small. Proof in Appendix 1.

Sometimes Our Guess is Too Big

If we don't preprocess our numbers, we can incur troubles:

6789:18

Using our standard guessing algorithm, A_guess is going to be 6 , 6 : 1 = 6, but 6*18=108 that is quite larger than 67.

In this case, we’ll try to reduce our guess until we find the correct result. We reduce our Q_i guess by 1 and try: 5*18, then 4*18, finally we find 3*18 < 67 so Q_i = 3.

Rather than reduce our guess by one, then multiply by B, we will use our intermediate result (108) and keep subtracting B (18) until Q_i become less than 67, as this will save a small amount of computing time: (my conjecture, not evidence based).

How Much Will it Cost to Arrive at the Correct Q_I?

1. 108-18=90
2. 90-18=72
3. 72-18=54

We had to do three more subtractions to find the right number, our initial guess was quite wrong, the correct number was a half of 108, and that was base 10, using base 2²⁵⁶ the trial-error procedure becomes impractical.

Normalize the Division

Luckily, the algebra book says, if \(B_m \geq \frac{base}{2}\) then we do 2 additional subtractions at most, I will not provide proof for this, I'd redirect to my book if somebody requests its name.

Suppose we are not so lucky and that \(B_m <\frac{base}{2}\) : The original division was:

e1: A = B * Q + R

We can preprocess the equation, we can legally multiply both sides by k, with the purpose of having B_m >= base/2

e2: kA = kB * Q + kR

Compare e1 to e2 expressions: Q does not change, what does change is R, we need to divide R by k before we return.

In our actual algorithm, we left shift until we got the leftmost bit of the leftmost digit to be 1, instead of doing expensive multiplications or divisions.

Return to the Example

6789 / 18

B_m is 1, so we keep multiplying by 2 (left shift on CPUs) until we have B_m greater than 5 (because the example is on base 10, on CPUs we need to have leftmost bit of B_m become 1).

1. 18 << 1 = 36
2. 36 << 1 = 72

we needed 2 shifts (the same as multiply by 4)

Also shift dividend

6789 << 2 = 27156

Now B_m is 7 that is >= (10/2).

The original division was 6789/18 (Q=377, R=3), now the division become 6789*4/18*4 (Q=377, R=3*4) which can be read as 27156/72 (Q=377, R=12)

The algebra book calls this a normalized division, Q does not change, R was multiplied by 4 as we run the new division, but now we are sure we have only a few guess to do.

CPU features like “Bit Scan Reverse” are available on low level languages, removing the need for a left-shift-loop: I have no evidence that CPUs BSR instructions are faster than a loop of bit shifts.

Review the Algorithm, Adding the Guess Algorithm and Remove Limitations

Now we will explicitly add the FindQn (guessing) subroutine to our algorithm, if B is normalized, the number of iteration of its internal loop is at most 2 but the remainder will be shifted, since input is normalized, we can also simplify the guessing routine.

The reviewed algorithm handles the case A <= B, to keep it simple the "Find Qn" subroutine is rendered as a function, but can be developed inline, it doesn't include the normalization process, let’s pretend this is the core algorithm and that by function composition, another part of code will handle normalization.

//TODO: On that chart, the long multiplication and the test is missing.

Final example with pseudocode.

Now we will proceed step by step through the reviewed algorithm: we’ll received normalized numbers as input so that leftmost of B is >= base/2

So instead of divide 6789 / 18, we will multiply both sides by 4 obtaining a new division 27156 / 72, our return value will then be R *4 and Q.

[Q]=empty,

//An = 271 because that is the first group of digits on 27156 that is > 72
[An] = Select as many digits from [A] such that [An] >= [B];

while([An] > [B])

FIRST ITERATION:

loop:
    Qn = 0;

    if(An < B) //271 < 72 so continue
      return zero;

    Bn = Leftmost of B; //7

    Aguess = Select as many digits from [An] such that Aguess >= Bn; //Aguess = 27
    Qn = Aguess / Bn; //Qn = 3

    Test = Qn\*B; //Test = 3*72 = 216

    while(Test > An) //216 > 271 is false so leave subroutine

    {

       Qn--;

       Test -= B;

    }

   return done;

   //end of subroutine:

   Append Qn to Q; //Q become 3

   Remainder = An = An - Test; //remainder become 271 – 216 = 55

   if(there are more digits in A) //there are more digits in A

   {

     Append next digit from A to An; //An become 555

      goto loop; //continue iteration

   }


SECOND ITERATION:

loop:
    Qn = 0;

    if(An < B) //555 < 72 false

      return zero;

    Bn = Leftmost of B; //7

    Aguess = Select as many digits from \[An\] such that Aguess >= Bn; //Aguess = 55
    Qn = Aguess / Bn; //Qn = 7

    Test = Qn\*B; //Test = 7*72 = 504

    while(Test > An) //504 > 555 is false so leave subroutine

    {

       Qn--;

       Test -= B;

    }

   return done;

   //end of subroutine:

   Append Qn to Q; //Q become 37

   Remainder = An = An - Test; //remainder become 555 – 504 = 51

   if(there are more digits in A) //there are more digits in A

   {

     Append next digit from A to An; //An become 516

      goto loop; //continue iteration

   }


THIRD ITERATION:

loop:
    Qn = 0;

    if(An < B) //516 < 72 false

      return zero;

    Bn = Leftmost of B; //7

    Aguess = Select as many digits from \[An\] such that Aguess >= Bn; //Aguess = 51
    Qn = Aguess / Bn; //Qn = 7

    Test = Qn\*B; //Test = 7*72 = 504

    while(Test > An) //504 > 516 is false so leave subroutine

    {

       Qn--;

       Test -= B;

    }

   return done;

   //end of subroutine:

   Append Qn to Q; //Q become 377

   Remainder = An = An - Test; //remainder become 516 – 504 = 12

   if(there are more digits in A) //there are no more digits in A so exit

   {

     Append next digit from A to An;

      goto loop; //continue iteration

   }

Check the result: 377*72+12=27156

But we wanted to divide 6789 / 18, the remainder has to be divided by 4; so check the result:

6789 = 18*377 + (12 / 4) = 18 * 377 + 3, that is correct.

A Computer Algorithm

A computer algorithm may vary depending on how you decide to represent a long number.

If you choose to use an array of unsigned integer to store a large number, here is a sample C version of the algorithm: I'm sorry if I do not paste here directly but it is too large.

Let me comment the above code a bit: the difficult part (all about division is difficult but can be tackled with some patience), is the implementation of the simple division algorithm, since my compiler does not support 128 bit integers, I had to write a very small x64 assembly routine to better use the hadrware, that makes the function not portable to x32 but since that code is so simple, you could write that support function for your hardware too.

.data

.code
    ;qword cpu_divide(
    ;     qword  low,         RCX
    ;     qword  high,         RDX
    ;     qword  divisor,             R8
    ;     qword * R,            R9
    ; );            
; RAX, RCX, RDX, R8, R9, R10, R11  VOLATILE
; RAX used to store cpu flags
cpu_divide proc
    mov rax, rcx    
    div r8
    mov qword ptr[r9], rdx
    ret
cpu_divide endp
end

Because it would be too time consuming for my x64 skills to write a full x64 implementation, I will publish the article with only that code; actually I created 2 C versions the first one is almost unreadable because I tried to do "optimization based on sentiment", the second one is more readable .

Aftermath

Here are some of the timings I got with the above implementations.

Algorithm Complexity

It is interesting to note how division is so much slower than multiplication and its speed depends essentially on the speed of inner multiplications, otherwise the algorithm looks linear time but it's not. All those multiplication are done with 1 digit times something, thus the multiplication algorithm is always executed in linear time, even using a simple elementary school multiplication algorithm is enough... probably faster than using any other algorithm, it is worth writing a specialized algorithm working on a fixed N*1 size and optimize as much as you can, the speed of division depends on that.

So the bell shape of the above chart shows that the worst performance happens when the dividend have size N and the divisor have size N/2.

This is explained by that:

When dividing N-digit by 1-digit you will get (ignoring subtractions):

• N CPU divisions
• N multiplications of size (1 * 1)
  totaling N + N * 1 operations => O(N)

When dividing N-digit by N-digit, you will get:

• 1 CPU division
• 1 multiplication of size 1 * N = N
  totaling 1 + N => O(N)

When dividing N-digit by M-digit (M < N) you will get:

• N-M+1 CPU divisions
• N-M+1 multiplication of size 1*M=M
  totaling (N-M+1) + (N-M+1) * M => O(M*N-M)
  since M<=N we whave that the maximum for M*N-M is when M = N/2

thus we can say best case complexity is \(O \left( N \right)\) worst case \(O \left( \left( \dfrac{N}{2} \right) ^2 \right){\implies}O \left( N^2 \right) \)

At the moment, I have no idea if better algorithms exists, I ordered some books in the hope to find an answer.

Appendix A

The Q_n guessed by the algorithm hereby proposed is greater than or equals to the correct Q_n

Since we are talking about a partial division, we only have two cases:

1. division of A/B where A and B have the same length
2. division of A/B where A have 1 digit more than B but its An, its leftmost digit, is less than Bn, the leftmost of B

Here's a picture of the possible 2 cases:

Showing only case 1, case 2 have similar proof.

Case 1

Hypothesis:

• H.1 \(A > B\)
• H.2 \(A, B\) have the same number of digits
• H.3 \(A_{n}\) is the leftmost digit of \(A\) in base \(b\)
• H.4 \(B_{n}\) is the leftmost digit of \(B\) in base \(b\)
• H.5 \(n\) is the number of digits of both \(A\) and \(B\)

Remember:

• R.1 \(A_{n} \geq B_{n}\) because of \eqref{def1} and \eqref{def2}
• R.2 \(A_{n} < b\) by definition of digit in base \(b\)
• R.3 \(A_{n}, B_{n}\) are non-zero (of most significant digit)

Let’s expand \(A\) and \(B\) into their positional representation:

our first guess \(Q\) is the single digit quotient of the simple division \(A_{n} / B_{n}\), such that \(A_{n}= B_{n} Q + R\)

Thesis

We want to proof that, for any couple \((A, B)\) for which it stands the initial hypothesis H, if we compute \(Q\) by using the proposed algorithm then \((Q+1)B>A\):

Proof

We must show that: \((Q+1) B > A\) Consider only the left part of the former inequality, and rewrite B using positional notation

The above notation shows, on the right part of the equation the string representation of the long number B multiplied by (Q+1) which is a single digit number by definition.

That is equals to (for distributive property of sum and multiplication)

Let me explain the former expression, it is a simplification to declutter the notation, we obtained a new positional expansion numeric string, where the rightmost least important digit is \([B_{1} * (Q+1) )\ MOD\ b]\) that we renamed as \([K_{1}]\).

While doing inner multiplications, we have a remainder that is propagated toward left, the propagation ends on the most significant part of the expression as the digit \(C\), which we don't know how bit it is but we know its less than \(b\).

Thus the left part of (eq5) is a 2 digit number to be appended to the left of the long \(K\) string. The multiplication modified all the digits, we don't know the value of the \(K\)'s digits but what is important is that we have a new number that have a new expansion that can have n or n+1 digits.

Now we got 2 positional notation strings (eq6) and (eq7):

Compare the above A string to the B string, to proof our thesis, we need to show that expression (eq6) > (eq7), \(\forall (A, B),\ H(A,B) \)

because \(0 \leq C < b\), I will ignore \(C\), to have a simpler expression

if you look at (eq6), (eq7) and (eq8) you will notice that, if we proof that \((eq8) > (eq7) \Rightarrow (eq6) > (eq7) \)

since the (eq8) is easier to show we'll go for it.

To show that (eq8) \(>\) (eq7), there are two possible cases:

Case 1: if

then it is sufficient to show that

Case2 : else we need to show that leftmost of (eq8) is strictly greater than leftmost of (eq7), in this case, we can ignore least significant digits and just have to proof (simpl1)

Given that, (case 2) is more restrictive than (case 1) and that \((case 2) \Rightarrow (case 1)\), it is enough to show (case 2). Thus we can ignore least significative digits of A and B (removing the less significant digits on both expressions), we should just proof \((eq11)\)

We can rewrite \((eq11)\) as (for distributive property)

Remove some parenthesis, reorder: \((eq13)\) is what we want to proof

now compare the inequality system

\((eq14)\) is the same as \((eq13)\), \((eq14)\) is what we knew, Q was obtained from the division \(A_{n}\ /\ B_{n}\), so \(A_{n} = Q * B_{n} + R\)

But \(R < B_{n}\) for the definition of division remainder, so (proof1) is true quod erat demonstrandum

History

• 11^th June, 2022: Published online