I thought it would be a very nice idea to start my blog with a small project I wanted to do since a long time. A small tool/solver of the n-body-problem. It’s not just only the interest of solving a challenging mathematical problem with modern C++. I also love clean, concise and readable code, which is also something I would like to train and share with this project. You can find the empty repository setup at GitHub. I will always try to tag the end state of the repository after each post of this blog series.
So lets start with the bare minimum of theory we need. We want to start with a simple example of two still standing masses (or stars if you like) which get attracted to each other. For the sake of simplicity we consider them as point masses which mean they are infinitesimal small, or in other words, they have no volume.
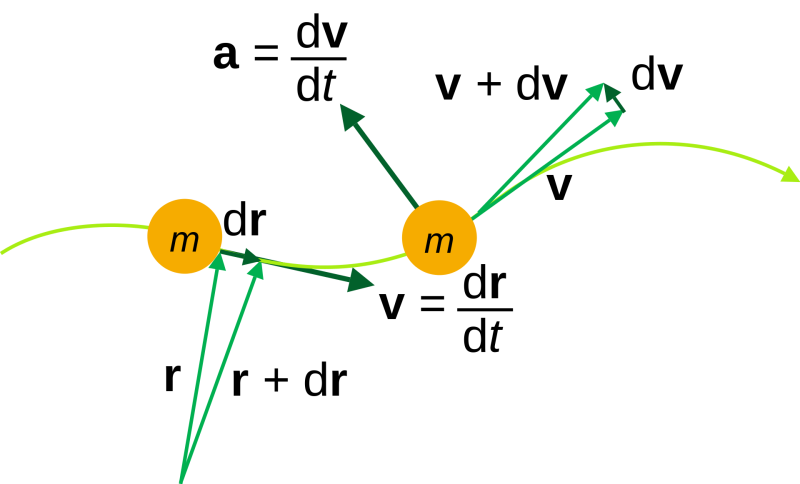 Kinematic quantities of a classical particle of mass m: position r, velocity v, acceleration a [Wikipedia]
Kinematic quantities of a classical particle of mass m: position r, velocity v, acceleration a [Wikipedia]
From the image above we can see that a particle is moving the path  , with its velocity
, with its velocity 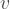 and accelerated by
and accelerated by  . From this point we get the equations of motion of one such point as
. From this point we get the equations of motion of one such point as

with  as the resulting position,
as the resulting position, 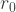 as the starting position,
as the starting position,  as the velocity,
as the velocity,  as the time step and
as the time step and  as the acceleration. We also know that the force is defined by the product of mass
as the acceleration. We also know that the force is defined by the product of mass  and the acceleration
and the acceleration 

We know as well that the force due to gravity between two masses can be calculated as

with the gravitational constant  the two masses of them and their distance
the two masses of them and their distance  . With the equations of the force and the force due to gravity, we can derive the acceleration
. With the equations of the force and the force due to gravity, we can derive the acceleration  a mass point is experiencing while he is attracted by another mass point.
a mass point is experiencing while he is attracted by another mass point.

As a result we get our final equation which is deriving the change of position of a mass point by its starting position, its velocity and its acceleration.

With this I will close this post and we will proceed next time with setting up a basic CMAKE example project which is building our solver library and a separate test library.
Did you like this post?
What are your thoughts on this post?
Feel free to comment and share the post.
