Introduction
This article examines the System.Collections.Generic (SCG) HashSet<T> in .NET and presents a replacement called FastHashSet<T> that is usually faster. FastHashSet<T> implements all of the methods and properties as HashSet<T> except for those involving serialization, so it is typically a drop-in replacement with some additional features. It uses C# 7.x ref returns and in (read-only ref) parameters for some performance improvements. SCG.HashSet<T> is the basis for (much of the code is the same as) the SCG.Dictionary<K, V>, so much of this discussion also applies to SCG.Dictionary<K, V>.
Extensive benchmarking is done with FastHashSet vs. SCG.HashSet and also the C5 generic HashSet. The SCG HashSet and FastHashSet use a hashing technique called Open Hashing (using Separate Chaining) as opposed to another hashing technique called Closed Hashing (Open Addressing). The C5 HashSet also uses Open Hashing, but does so with a single hash array of items. It then links the items together by using separate class objects (reference types) with a next pointer.
Open Hashing with separate chaining, in some implementations, uses two arrays (one called buckets and another called slots). The buckets is just an array of indices into the slots array, which holds the actual values. All values with the same 'hash code mod (%) the buckets array size' are in the same bucket (chained list of values in the slots array). This is how the SCG HashSet and FastHashSet are implemented.
Closed Hashing, in some implementations, uses a single buckets array. The 'hash code mod (%) the array size' is used as the initial index to look for the value. If not found at this index, there is some determined method to "probe" for the value in the buckets array to find it near to this initial index. I don't know of any Closed Hashing implementations of a HashSet in .NET, but there are plenty in C++. See this interesting article on hash table implementations and methods in C++ (https://probablydance.com/2017/02/26/i-wrote-the-fastest-hashtable/).
There are benefits, and variations, of both methods. Closed Hashing has the benefit of using only a single array and it also can benefit from locality of reference (increasing the probability of accessing CPU cache instead of main memory) as long as the probing doesn't wander too far from the initial calculated index. Open Hashing can benefit from a fewer number of value equals comparisons, because we are always only comparing the values of items with the same hashed index (usually determined by the hash code mod (%) the buckets array size). If the equals comparison for the type of objects being stored is relatively expensive, then this is a great benefit.
There are a few other .NET generic containers that are looked at from a performance perspective. These are a sorted List<T> that allows binary search to find contained items, and also the SortedSet<T>.
Background
The idea behind FastHashSet started when I was trying to find a way to store structs in a HashSet or Dictionary with reference counting. What I mean by this is I need to store some structs so that if they are found, we need to either increment or decrement their reference count. I could not find a highly performant way to do this with the existing System.Collections.Generic HashSet or Dictionary. A similar scenario occurs frequently for me when I have to get a total for certain objects.
The reason this is costly for System.Collections.Generic HashSet or Dictionary is simple: you must use a reference type (class) in order to find the object and then be able to change the object or its value (reference count or total) with a single method (Add). If using value types (structs), you need to call Add and if Add returns false because the value is already present you need to Remove, change and then Add again. This results in poor performance.
Method 1: Use class objects instead of structs and store the reference count within the object itself and use a HashSet.
This works except that the class objects must be allocated on the heap, while structs do not. If there are many objects, then there will be many heap allocations and this can be costly in terms of memory and also cause extra time during GCs. For small objects, a struct should have better performance than a class, both in terms of CPU time and also memory use.
Using the Code
The code for FastHashSet can be found at https://github.com/Motvin/FastHashSet.
The machine I used for benchmarking has an Intel Core i7-8700K, uses Windows 10 64 bit, and the code was also run as 64 bit processes using the RyuJit compiler. .NET Framework 4.7.2 was used for all benchmarks (unless otherwise noted).
I used BenchmarkDotNet for most of my benchmarking, although I found some cases where the results seemed off with BenchmarkDotNet (it was showing significant spikes in some of my graphs where they should have been mostly linear), so I also created my own performance testing database (under the Perf repository) to verify the results of my benchmarks.
Below is my BenchmarkDotNet run to compare reference counting using methods in FastHashSet with a small struct vs. the same reference counting using the SCG HashSet with a small class. The ratio was different at different values of N (for example, the ratio was .43, FastHashSet was over twice as fast, for N = 1,000,000, but at N=9,000 the FastHashSet ratio was only .81). Other ratios were between these two, so to summarize, FastHashSet reference counting was a little less than twice as fast as the SCG HashSet implementation.
[RyuJitX64Job]
public class RefCountHashSetVFastHashSet
{
public int[] a;
[Params(10, 100, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10_000, 20_000,
30_000, 40_000, 50_000, 60_000, 70_000, 80_000, 90_000, 100_000, 1_000_000, 10_000_000)]
public int N;
[GlobalSetup]
public void Setup()
{
a = new int[N];
Random rand = new Random(89);
int nDiv2 = N / 2;
for (int i = 0; i < a.Length; i++)
{
a[i] = rand.Next(1, nDiv2); }
}
[Benchmark(Baseline = true)]
public void SCGRefCnt()
{
HashSet<SmallClassIntVal> set = new HashSet<SmallClassIntVal>();
for (int i = 0; i < a.Length; i++)
{
SmallClassIntVal v = new SmallClassIntVal(a[i], 1);
if (set.TryGetValue(v, out SmallClassIntVal v2))
{
v2.refCountOrSum++;
}
else
{
set.Add(v);
}
}
for (int i = a.Length - 1; i >= 0; i--)
{
SmallClassIntVal v = new SmallClassIntVal(a[i], 1);
if (set.TryGetValue(v, out SmallClassIntVal v2))
{
if (v2.refCountOrSum == 1)
{
set.Remove(v);
}
else
{
v2.refCountOrSum--;
}
}
}
}
[Benchmark]
public void FastRefCnt()
{
FastHashSet<SmallStructIntVal> set = new FastHashSet<SmallStructIntVal>();
for (int i = 0; i < a.Length; i++)
{
SmallStructIntVal v = new SmallStructIntVal(a[i], 1);
ref SmallStructIntVal v2 = ref set.FindOrAdd(in v, out bool isFound);
if (isFound)
{
v2.refCountOrSum++;
}
}
for (int i = a.Length - 1; i >= 0; i--)
{
SmallStructIntVal v = new SmallStructIntVal(a[i], 0);
ref SmallStructIntVal v2 = ref set.FindAndRemoveIf
(in v, b => b.refCountOrSum == 1, out bool isFound, out bool isRemoved);
if (!isRemoved && isFound)
{
v2.refCountOrSum--;
}
}
}
}
public struct SmallStructIntVal : IEquatable<SmallStructIntVal>
{
public int myInt;
public int refCountOrSum;
public SmallStructIntVal(int i, int refCountOrSum)
{
myInt = i;
this.refCountOrSum = refCountOrSum;
}
public override int GetHashCode()
{
return myInt;
}
public override bool Equals(object obj)
{
if (obj.GetType() != typeof(SmallStructIntVal))
{
return false;
}
return Equals((SmallStruct)obj);
}
public bool Equals(SmallStructIntVal other)
{
return (myInt == other.myInt);
}
public static bool operator ==(SmallStructIntVal c1, SmallStructIntVal c2)
{
return c1.Equals(c2);
}
public static bool operator !=(SmallStructIntVal c1, SmallStructIntVal c2)
{
return !c1.Equals(c2);
}
}
public sealed class SmallClassIntVal : IEquatable<SmallClassIntVal>
{
public int myInt;
public int refCountOrSum;
public SmallClassIntVal(int i, int refCountOrSum)
{
myInt = i;
this.refCountOrSum = refCountOrSum;
}
public override int GetHashCode()
{
return myInt;
}
public override bool Equals(object obj)
{
return Equals(obj as SmallClassIntVal);
}
public bool Equals(SmallClassIntVal other)
{
if (other == null)
{
return false;
}
return (myInt == other.myInt);
}
}
FastHashSet vs. SCG HashSet vs. C5 HashSet
SCG HashSet has an Odd Method of Resizing
The SCG Hashset oddly resizes its internal slots array to be the same size as the internal buckets array. It resizes to a capacity that is the next highest prime that is greater than double the previous capacity. This is odd because it makes sense to keep the buckets array at a prime number size because creating a hash index that is mod a prime number can avoid some patterns that can make different values hash to the same index which causes larger, more expensive item chains. It is typical to use a prime size for the buckets array for this reason.
But there is no reason to keep the slots array the same size as the buckets array. Doing so is equivalent to using a load factor of 1.0 as a minimum, and this can produce longer item chains which slow down Adds and Contains. A minimum load factor of about .75 is more typical to keep item chain sizes small. It's also more difficult to predict when a resize will occur. It's much easier to predict resizes when a resize occurs whenever the count of items first exceeds a power of 2. The power of 2 resizing is the method used for the SCG List<T>, Stack<T>, Queue<T>, and others.
FastHashSet resizes the slots array to the next power of 2 whenever it becomes full and keeps the buckets array at a .75 load factor minimum. This means the buckets array size is kept at about 1.33 larger than the size of the slots array, which can reduce the number of long chains.
SCG HashSet Allocates and Uses the Entire Buckets Array when Specifying Initial Capacity in Constructors
One of the things I learned when benchmarking the different hashset implementations is that CPU caches really matter for performance. When using the SCG HashSet's constructor (HashSet(int capacity)), the HashSet allocates, and also uses, a buckets array that accommodates this size.
Using the entire buckets array can be really bad for performance. For example, if this is called with a capacity = 10,000,000, then the buckets array will be allocated with that size, but also any items added will be distributed within this array more or less randomly. This gives really bad cache locality, which causes poor performance. The odds that items being added are in the same cache lines as previously added items is much smaller than if the buckets array was only initially using a fraction of its allocated size.
FastHashSet uses a technique where it allocates the size of the buckets array to accommodate the 10,000,000 items without having to resize, but initially only uses a fraction of that large size. The 3 values (below) were chosen while testing on my particular PC, so they might not be the best for other machines, but I think any values will probably be better than doing what the SCG HashSet does. There is a hit when one of the sizes below is exceeded because the buckets array items must be rehashed at that point, but this is generally much faster than allocating (and using) the entire buckets array from the start.
private static readonly int[] bucketsSizeArrayForCacheOptimization = { 3_371, 62_851, 701_819 };
FastHashSet Uses a Simple Array for Small Sets
FastHashSet uses an array implementation with linear search at small set capacities (<= 8 items). The array implementation avoids the overhead of hashing completely and that's why it's faster at small sizes. During my tests, it may have been faster even up to 10 or so items, but I wanted to switch from the non-hashing array implementation to a hashing one at a power of 2, so I chose 8 items as my max for non-hashing.
The reason why I chose implementing this performance enhancement is because of the comment in the SCG .NET Core HashSet code that states that "hashtables tend to contain only a few elements". So I thought adding something that made FastHashSet faster for a few elements would be useful. This code is contained within an #if/#endif, so this code can easily be removed by enabling a #define constant, if you know your particular use won't benefit from this.
SCG HashSet and FastHashSet Zero out the High Order Bit in the Hash Code When Creating the Index
When I was testing adding random ints between int.MinValue and int.MaxValue, I noticed my FastHashSet performance wasn't as good vs. SCG HashSet when the integers were all positive. It turned out this was because I was doing something like (if (hashIndex < 0) hashIndex = -hashIndex;
This works, but it has very poor branch prediction performance when the hash codes are randomly alternating between positive and negative values. Looking at the SCG HashSet code for .NET Core, I saw how they got around this. They basically zero out the high order bit of the hash code so that the generated index value is always positive. This is something I added to FastHashSet as well.
Benchmark Results of Adding Integers
Random integers from int.MinValue to int.MaxValue were added to the containers with the Add method and benchmarked with BenchmarkDotNet. This was done in groups of N values (from 1 to 100 integers, from 100 to 1,000 integers, etc.) and each group was graphed. It turned out the C5 HashSet performance was about 4 times slower than the other HashSets and this made the graphs less readable, so I included the series for adding integers to a List<int>, which was then sorted after the adds were done. This is in preparation for a binary search.
SortedSet<T> Adds were always much slower than the hashsets, so the series for this was not shown in any graph.
The graph below shows that FastHashSet generally outperforms SCG HashSet except on and slightly after when a resize is done. The capacity for FastHashSet is kept at a power of 2 (8, 16, 32, 64, etc.) and a resize is done for an add that requires more space than this capacity. So you can see the large increase at N = 65 for FastHashSet because it needs to resize to the next capacity (= 128) to accommodate adding the 65th integer. Resizes for hashsets are expensive, so it's best to avoid them if possible by trying to determine how many items will be contained in the hashset and using the constructor that takes an initial capacity.
List<int> with a sort after the Adds is faster than the hashsets and this continues into the next graph until it becomes slower at about 700 Adds.
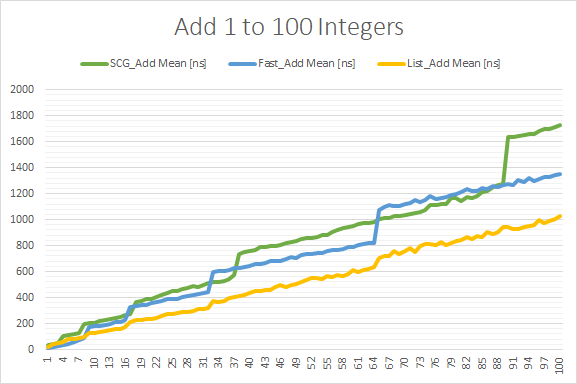
The graph below shows that FastHashSet is slightly faster than HashSet and starts to beat List<int> with a sort at about 700 Adds.

The graph below shows that List<int> with a sort after adding is no longer close to as fast as either hashset. It does, however, become the fastest again at about 7.5 million Adds. This is probably because the hashsets tend to have lots of CPU cache misses at these large sizes.
At about 8,700 Adds, you can see a spike in the graph for the SCG series. This appears to be an issue with benchmarking using BenchmarkDotNet. If the spike were real, it would be like saying that adding 8,700 integers and then an additional 1,000 integers took less time than adding the original 8,700 integers. This is why I think you should always try to verify your benchmarks by running with multiple benchmarking tools, or at least running multiple times with the same benchmarking tool and averaging the results.

The graph below shows that FastHashSet usually outperforms SCG HashSet for this range of Adds.

One interesting thing to note about doing a single Add with a hashset with size = 10 million integers takes about 140 nano seconds, but the same single Add with a hashset with size = 100 integers is about 16 nano seconds. This is because the memory references in the smaller hashset tends to use the CPU caches effectively, where the larger hashset tends to have more CPU cache misses.
Benchmark Results of Integer Contains
Contains benchmarks were done in groups of N Contains, for example, from N = 1 to N=100, etc. Contains was done after adding the maximum N for the group number of items to the collection first. The array of integers that Contains used consisted of 50% items that existed in the collections and the other 50% did not exist.
As for the hashsets, FastHashSet took an average of 92% of the time of the other 2 hashsets for the group from 1 to 100, but in the graph below, the C5 HashSet overtakes both the SCG and FastHashSet at about 600 Contains.
FastHashSet start to outperform the C5 HashSet again at about 100,000 Contains.

The List<int> and SortedSet<int> Contains were typically 2 - 4 times slower than any of the hashsets, so the series for these was not shown in the graphs. Even with List<int> being the fastest at Add and sort up to about 700 items, it's difficult to find a situation to use it with binary search above a hashset because of its relatively poor Contains performance.
There are some special situations, though, where List<int> should be preferred to a hashset. For example, in situations where you need the items sorted anyway, or if you already have sorted items. Also, with binary search, it's possible to find the lesser or greater value if the exact value was not found. Also, List<int> will have the least memory use of any of these containers, so if that is important then List<T> might be a consideration over a hashset.
SortedSet<T> doesn't have much going for it compared to hashsets or List<T>, but I've heard that the performance for SortedSet<T> has been much improved in .NET Core, so if you're using that environment, it might be worth benchmarking to see if it's worth using.
Testing FastHashSet
To test FastHashSet, I grabbed the .NET Core xUnit tests from BitBucket and changed them to reference FastHashSet instead of HashSet. The code currently passes over 37,000 tests of these tests. The tests involving serialization/deserialization were removed since this was not implemented in FastHashSet.
I also added a few xUnit tests to test the additional methods added for FastHashSet.
These new methods are:
Add and Contains using an in parameter to allow for efficient struct param passing in these methods.
bool RemoveIf(in T item, Predicate<T> removeIfPredIsTrue)
ref T FindOrAdd(in T item, out bool isFound)
ref T Find(in T item, out bool isFound)
ref T FindAndRemoveIf(in T item, Predicate<T> removeIfPredIsTrue,
out bool isFound, out bool isRemoved)
List<ChainLevelAndCount> GetChainLevelsCounts(out double avgNodeVisitsPerChain)
void ReorderChainedNodesToBeAdjacent()
HashSet Implementations vs. Binary Search of a Sorted List<T> vs. SortedSet<T>
Although a hashing collection is generally regarded as the fastest when determining if a value is contained within a collection, there are some cases when a sorted List<T> using binary search is faster.
Conclusion
This article shows that using a hashtable/hashset/dictionary collection is usually the fastest for item lookup (Contains), and Adding items and Removing items. The problem is that the current implementation of the SCG HashSet<T> is adequate for most uses, but not extremely good for cases that need the utmost in performance.
.NET is behind other languages (like C++), that have many available hashtable implementations that are highly optimized for performance in various aspects (see link at the top of the article).
FastHashSet may be an implementation that can be useful for these high-performance use cases, especially in situations like reference counting or summing values where it is almost 2 times faster than the SCG HashSet. It is easy to use the code and modify it to fit a particular situation. FastHashSet is contained in a single file (FashHashSet.cs), and has a few #ifs that allow for customization. It would be easy to take the source code and produce implementations that were even faster by removing the generic parts and focusing, for example, on just containing ints.
History
- 23rd April, 2019: Initial article submitted
