A Conceptual AI Neural Network - Data Network Load Balancing with Ant Colony Optimisation

• Download source code - 791.6 KB

Introduction

Ants first evolved around 120 million years ago, took form in over 11,400 different species, and are considered one of the most successful insects due to their highly organised colonies, sometimes consisting of millions of ants.

One particular notability of ants is their ability to create "ant streets". Long, bi-directional lanes of single file pathways in which they navigate landscapes in order to reach a destination in optimal time. These ever-changing networks are made possible by the use of pheromones which guide them using a shortest path mechanism. This technique allows an adaptive routing system which is updated, should a more optimal path be found or an obstruction placed across an existing pathway.

Computer scientists began researching the behaviour of ants in the early 1990s to discover new routing algorithms. The result of these studies is Ant Colony Optimisation (ACO), and in the case of well implemented ACO techniques, optimal performance is comparative to existing top-performing routing algorithms.

This article details how ACO can be used to dynamically route traffic efficiently. An efficient routing algorithm will minimise the number of nodes that a call will need to connect to in order to be completed thus; minimising network load and increasing reliability. An implementation of ANTNet based on Marco Dorigo and Thomas Stützle has been designed, and through this a number of visually aided tests were produced to compare the genetic algorithm to a non-generic algorithm. The report will finally conclude with a summary of how the algorithm performs and how it could be further optimised.

Background

Electronic communication networks can be categorised as either circuit-switched or packet-switched. Circuit-switched networks rely on a dedicated connection from source to destination, which is made once at start-up and remains constant until the tear-down of the connection. An example of a circuit switched network would be the British Telecoms telephone network. Packet-switched networks work quite differently, however, and all data to be transmitted is divided into segments and sent as data-packets. Data-packets can arrive out of order in a packet-switched network, with a variety of paths taken through different nodes in order to get to their destination. The internet and office local area networks are both good examples of packet-switched networks.

A number of techniques can be employed to optimise the flow of traffic around a network. Such techniques include flow and congestion control, where nodes send packet acknowledgements from destination nodes to either ramp-up or decrease packet transmission speed. The area of interest in this report concentrates on the idea of network routing and routing tables. These tables hold information used by a routing algorithm to make a local forwarding decision for the packet on the next node it will visit in order to reach its final destination.

One of the issues with network routing (especially in very large networks such as the internet) is adaptability. Not only can traffic be unpredictably high, but the structure of a network can change as old nodes are removed and new nodes added. This perhaps makes it almost impossible to find a combination of constant parameters to route a network optimally.

Routing Algorithms

Packet-switched networks dynamically guide packets to their destination via routing tables stored in a link state and are selected via a link state algorithm.

A link state algorithm works by giving every node in the network a connectivity graph of the network. This graph depicts which nodes are directly connected. Values are stored for connected nodes in a map which represents the shortest path to other nodes. One such link state algorithm used in network routing is Dijkstra's algorithm. When a path between two nodes is found, its weight is updated in the table. Should a shorter path be found, the new optimal weight will be updated to the table, replacing the old value.

The algorithm allows traffic to be routed around the network whilst connecting to the least number of nodes as possible. The system works, but doesn't take into account influx of traffic and load balancing.

Introducing ANTNet

By replacing Dijkstra's algorithm with a generic algorithm, paths taken by calls could be scored by how short of a path they took; that way, if they were queued on a busy network, they would perform badly. Consequently, other paths would score relative and be chosen. This would work in real time, and allow the routing system to adapt as packets are transmitted. ANTNet uses virtual pheromone tables much like when an ant follows a path, dropping pheromone to re-enforce it. The quicker the ants move down a path, the more throughput of ants, thus a greater concentration of pheromones. In the same way, pheromone tables in ANTNet allow fast routes to score a higher chance of being selected, whilst the less optimal route scores a low chance of being selected.

The idea behind ANTNet is when a call is placed, an Ant will traverse across the network using a link-state deterministic algorithm. Every node holds a pheromone table for all other nodes of the network. Each pheromone table holds a list of table entries containing all the connected nodes of the current node.

The Algorithm

To begin with, each possible path has an even likelihood of being chosen. An ant is placed on a network of 4 nodes, with the source node 1 and destination node 2. A chance mechanism is invoked and a path is chosen.

In this case, node 2 has been selected [Figure 3.2] and the ant arrives at its source destination.

The ant then moves and updates the pheromone tables for the visited nodes with a higher (and more mathematically biased) value. This would be calculated for Figure 3.2 and Table 3.2 in the following way:

• Node 2 was the final destination
• It took 1 hop to get to its destination
• Divide 1 (hop) by 100: 100%
• Add 100 to the probability value of node 2 (currently 33.3333): 133.3333
• Add the values of the other nodes to 133.3333 (133.3333 + 33.3333 + 33.3333): 200 (approximately)
• Calculate the ratio: ratio = 100/200 0.5
• Set the probability of the node to its current value multiplied by the ratio
  • Node 2: 133.3333 * ratio (0.5) = 66.6666%
  • Node 3: 33.3333 * ratio (0.5) = 16.6666%
  • Node 4: 33.3333 * ratio (0.5) = 16.6666%
• Node 2 (66.6666%) + Node 3 (16.6666%) + Node 4 (16.6666%) = 99.9999%

The system isn't 100% accurate as the total will never add up to exactly 100%, but it will be close enough to allow accuracy within the level required.

The following diagram depicts how the path and pheromone table after the update has taken place.

The Program

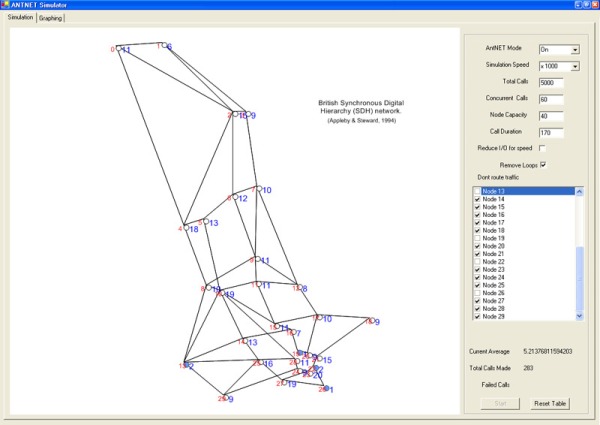
For the purpose of this program, a bi-directional, un-weighted topological network consisting of 30 nodes has been created, and closely resembles the British Synchronous Digital Hierarchy (SDH) network. After a basic number of parameters have been set, the simulation is run. Firstly, all pheromone tables are defaulted to equal weights, and then calls are generated and placed on the network. Initially, the routes chosen are random. If a call cannot connect to a node, it is forced to wait, and the wait counter is enumerated to reflect the quantum (in timer ticks). Once a node has reached its destination node, it will work its way backwards, altering the local node's pheromone table as it traverses. The shorter the route taken, the greater increase in probability given to its table entry in the pheromone table. This happens repeatedly until the weight of the fastest node is shifted such that slower routes have a very low probability of being chosen.

Note: In order to compile and run the program, you will need to download dotnetcharting from dotnetcharting.com

Program Features

• ANTNet On/Off - Switches the algorithm on and off
• Simulation speed - 1 tick p/s - 1,000 tick p/s (or as near speed as the system can run)
• Total calls to make - Number of completed calls before simulation termination
• Maximum concurrent calls - Number of calls allowed at the same time
• Node capacity - The number of calls a node can route at once
• Call duration - The length (in ticks) of a call
• Reduce I/O - Bypasses the network visualisation to increase simulation speed
• Return on connection - Returns the node immediately to source after connection
• Real-time network load visualisation - View node ID, capacity, and routing state (blue = OFF)
• Graphing facility with labeling and simulation overlay
• Render pheromone tables to HTML

Classes

• MainForm - The GUI for the application
• DrawPanel - The real-time network visualisation custom control
• Global - Contains static variables that are accesses by the application
• Node - Represents a node and holds an array of PheromoneTable objects for routing
• Call - Represents a call on the network and holds a source and destination node
• Simulation - Represents a completed simulation and is used for creating graphs
• PheromoneTable - A routing table for a Node

The network contains 30 Nodes, and each Node contains an array of PheromoneTable objects, one for every other Node in the network (29). Every PheromoneTable contains an array of TableEntrys, one for each Node connected to the current Node.

The following diagram represents the relationships between classes in the program:

Updating the pheromone table:

// returns the next Node of the path
        public int ProbablePath(ArrayList VisitedNodes)
{
    // create a random generator
    Random r = new Random(Global.Seed);

    double val=0;
    double count = 0;
    double Lastcount = -1;

    ArrayList tempTEVector=new ArrayList();

    // loop through all the connected nodes
    for(int i=0;i<tableEntry.Length;i++)
    {
        // has the node been visited?
        bool v=false;

        //loop through all the visited nodes
        for(int j=0;j<VisitedNodes.Count;j++)
        {
            // if the ID's match then this node has alrady been visited
            if(tableEntry[i].NodeID==(int)VisitedNodes[j])
                v=true;
        }
        
        // If v is false, then the node hasn't been visited.. so Add
        if(!v) 
        {
            // get the node
            Node n = Global.Nodes[tableEntry[i].NodeID];

            // if the node is accepting connections
            if(!n.FullCapacity)
            {
                // add the node as a possible candidate
                tempTEVector.Add(tableEntry[i]);
            }
        }
    }
    
    // if all connections have been visited
    if(tempTEVector.Count==0)
    {
        // loop through all the connected nodes
        for(int i=0;i<tableEntry.Length;i++)
            tempTEVector.Add(tableEntry[i]);
    }

    // get the ceiling amount for probabilities
    for(int i=0;i<tempTEVector.Count;i++)
        val+= ((TableEntry)tempTEVector[i]).Probablilty;

    //create random value
    val = r.NextDouble()*val;

    // loop through the temp Table Entries
    for(int i=0;i<tempTEVector.Count;i++)
    {
        // increment the count on each loop
        count += ((TableEntry)tempTEVector[i]).Probablilty;

        // if the random value falls into delegated range,
        // then select that path as the next node
        if(val>Lastcount && val < count)
            return ((TableEntry)tempTEVector[i]).NodeID;

        // get the value of the last count
        Lastcount=count;
    }

    // method should never return here
    return -1;
}

Returning the next node via the pheromone table:

// updates the probabilities of the pheromone table by multiplying the selected 
// nodes probability by a radio of  newVal
public void UpdateProbabilities(double newVal, int EntryTableNodeID)
{
    TableEntry t;
    double total=0;

    // loop through all the table entries
    // get the total enumeration of probabilities and add the new value.
    // Since this total will be more than 100, a ratio multiplication is
    // applied. Although these values will not equate to exactly 100%, floating
    // point calculations will be accurate enough 
    // at least 99.99999% which is satisfactory
    for(int j=0;j<tableEntry.Length;j++)
    {
        t = tableEntry[j];

        // enumerate the total Probablilty
        total += t.Probablilty;
    
        // if the table entry matches the id of the chosen node path
        if(EntryTableNodeID==t.NodeID)
        {
            // add the new value to the total
            total += newVal;
            t = tableEntry[j];
            // add the new value the current value of the selected path
            t.Probablilty += newVal;
        }
    }

    // calculate the ratio for the multiplication
    double ratio = 100/total;

    // loop through each table entry and multiple the current probability
    // by the new ratio
    for(int j=0;j<tableEntry.Length;j++)
    {
        tableEntry[j].Probablilty *= ratio;
    }

    // this will enumerate all the values to 99.99999%
}

// Constructor takes a node to represent and a list of all connected nodes off the
// calling node
public PheromoneTable(Node n, int[] conns)
{
    this.NodeID = n.ID;

    // create a tableEntry array the same length as the number of connections
    this.tableEntry = new TableEntry[conns.Length];

    // create a new tableEntry for each connection
    for(int i=0;i<conns.Length;i++)
        tableEntry[i] = new TableEntry(conns[i]);

    // set default equal values
    for(int i=0;i<conns.Length;i++)
        tableEntry[i].Probablilty = (100 / (double)conns.Length);
}

Simulation Results

The following tests will illustrate how the ANTNet algorithm affects the routing of traffic. These tests will show the effectiveness of the algorithm against the system running without ANTNet. Since it is possible to switch nodes on and off, a number of test comparisons will be done to show how ANTNet can improve the routing of a network when paths are no longer valid and new routes have to be chosen.

These tests have been run with the following parameters:

• ANTNet On
• Simulation speed -1,000 tick p/s
• Total calls to make - 5000
• Maximum concurrent calls - 60
• Node capacity - 35
• Call duration - 170 (the length (in ticks) of a call)
• Reduce I/O - bypasses the network visualisation to increase simulation speed
• Return on connection - returns the node immediately to source after connection

ANTNet vs. non-ANTNet

The first test contains two simulations:

• Simulation 1 (Orange) - ANTNet algorithm OFF
• Simulation 2 (Blue) - ANTNet ON

From this simulation, it is clear that even by the first 500 calls completed, ANTNet has reduced the average number of hops by approximately 1.5 nodes. This is made more apparent by the end of the simulation where the best paths are made more biased as a choice, and are re-enforced as the optimal route, resulting in ANTnet improving network performance by almost 3.5 hops.

To view the algorithm from a different perspective, the following graph depicts the system running with the ANTNet algorithm off and then activated on the 2,000^th call. This can be identified by a label, and follows with a decline of average hops by almost 2.

Loop Elimination

Before an ant returns back to its source node, an optimisation technique of loop elimination can be invoked. The problem with loops is that they can receive several times the amount of pheromones than they should, leading to the problem of self re-enforcing loops.

Figure 5.3 shows two simulations:

• Simulation 1 (Orange) - Loop elimination OFF
• Simulation 2 (Blue) - Loop elimination ON

From this test, loop elimination has reduced the average number of hops by 1 node with a much more stable adaptation. This would mean that when alternative paths must be chosen, the loop elimination algorithm responds much faster than the regular implementation.

Note: Both lines show the actual number of nodes traversed, and not the number after loop removal.

Adaptivity

It is important to simulate how the network adapts when nodes are removed from the network. Static routing tables may hold the shortest path, but they don't necessarily take into account network traffic and nodes that are offline. Three simulations have been run on the program to display how the system adapts compared to a non-adaptive algorithm.

Simulation 1 (Orange)

This is a normal run of the simulator to create optimised pheromone tables for the next two simulations.

Simulation 2 (Blue)

Adaptive algorithm switched OFF.

Nodes 14, 15, and 17 are switched off as these are the main northern access hubs into London, so traffic needs to be diverted to the west of England. Since the network is non-adaptive, the pheromone tables are biased towards nodes that have been taken offline and subsequently being continuously redirected and taking longer journeys every time. This increase is displayed in Figure 6.4 by the blue line.

Simulation 3 (Green)

Adaptive algorithm switched ON.

Nodes 14, 15, and 17 are still switched off, but since the network is now set to adaptive, the pheromone tables are readjusted and the system learns alternative routes. This can be seen in Figure 6.4 by the green line.

Recommendations

If anyone has any questions, bugs, or suggestions, then please make a comment.

References

1. Appleby, S., Steward, S. (1994). Mobile software agents for control in telecommunication networks. In BT Technology Journal, Vol. 12, No.2.
2. ANTNet: A Mobile Agents Approach to Adaptive Routing. Gianni Di Caro and Marco Dorigo.
3. Ant-based load balancing in telecommunication networks. Ruud Schoonderwoerd1,2, Owen Holland3, Janet Bruten1, and Leon Rothkrantz.
4. Data Networks. Bertsekas, D., Gallager, R. (1992).

History

• 4^th May, 2006: Initial version
• 17^th August, 2010: Update
• 10^th January, 2023: Update