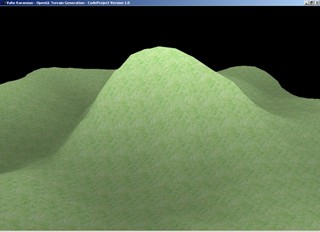
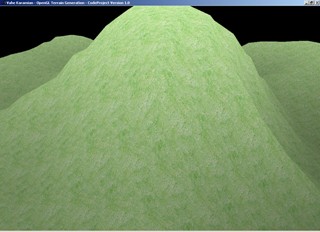

Introduction
I have always been interested in computer graphics and their applications. Data representation and visualization is one of the main areas of HCI (Human Computer Interaction), and the better you make the interaction between a machine and a human, the more productivity will be generated by both the human and the machine. I had some experience with OpenGL during my undergraduate studies while attending the California Polytechnic University. Unfortunately, I never got a chance to pursue the more advanced features of the OpenGL library, given my time and work responsibilities.
You can find more about OpenGL at www.opengl.org. There are also a bunch of good literature available on the topic of Computer Graphics and OpenGL that you can refer for further advancements. Please check the Background/Reference section for a list of some reference material that I have used, in general, for computer graphics.
The following project is a very simple example demonstrating how to generate a terrain based on a bitmap file. The objective of the project is to generate a three dimensional terrain based on some data file. Please note, that this could have been any data file, but for the purpose of our example, we are going to be using a 32x32 dimensional bitmap file. We could have easily used a text file, and defined logic for each word or letter to represent it graphically.
The project also contains a good Windows framework that can be used for your other OpenGL applications. The current project allows you to rotate the camera using your mouse.
Once again, this is a simple approach to terrain generation, which can be a very difficult task in complex environments.
Background/Reference
Since Computer Graphics is kind of an advanced topic, it is necessary to have at least some king of understanding and exposure to the concepts and theories in the field. However, this does not mean that you will not be able to use the following code or understand it. I have made it as simple as possible, and hopefully, it will give you a good start, or some additional source of information that you can use for your projects. Also, please note that you will need to have a good understanding of C/C++ programming.
Some books I have used for learning Computer Graphics and OpenGL programming:
Books I used while attending the California Polytechnic University:
- OpenGL Programming Guide, or better know as the Red Book.
- Computer Graphics Using OpenGL, 2nd Edition.
Books I used while attending the California Lutheran University:
- OpenGL: A Premier, 2nd Edition.
- Interactive Computer Graphics: A Top-Down Approach Using OpenGL, 4th Edition.
What is a Terrain?
Some background information on a terrain and their uses in a game application: A terrain in an environment is one of the most critical components in the scene that is being rendered. It could easily be the largest 3D object in the project. Rendering the terrain can become a daunting task, taking the most time to render in a scene. To keep the terrain engine running in real time can be a difficult task, and it requires some thought out processes and modeling for it to be sufficient.
To be effective, the terrain needs to meet a number of requirements, many of which can be contradicting each other. A terrain should appear to be continuous to the end user, yet the mesh should be simplified or culled where possible, to reduce the load on the graphics card.
In a gaming system, for example, some engines draw the terrain just beyond the point a player can reach, and then use a terrain drawn onto a skybox to simulate hills or mountains in the distance. The terrain should appear realistic to the setting for the environment, yet this can be taxing on the video card, and a balance needs to be maintained. Detail textures are often used close to the camera, allowing the areas further off to be rendered more quickly.
What is a Height Map?
The first thing required for terrain rendering is a representation of the terrain's shape. While there are a number of structures that can be used to perform the job, the most widely used is the height map. Others include: NURBS, which can be maintained through a number of control points, and voxels, which allow for overhangs and caves.
There is one drawback to a height map, and that is, for every point on the XZ-plane, there can only be one height value. You can see that this limits the representation of overhangs and caves by a height map. This can be overcome by using two separate models.
Another drawback is that height maps take a large amount of memory, as each height must be represented. On the other hand, height maps lend themselves to the creation of regular meshes easily. It is also easy to determine the height at any given location, which is useful for collision against the terrain as well as laying dynamic shadows onto the terrain.
A height map is represented by a 2D array of values, where for any point (X, Y, Z), the X and Z are the indexes into the array, and the value of the array is the Y value which is equivalent to the height value.
The following is an example of such a representation:
int height[5][5] ={
{ 0, 0, 1, 1, 2 },
{ 0, 1, 2, 2, 3 },
{ 0, 1, 3, 2, 3 },
{ 0, 1, 2, 1, 2 },
{ 0, 0, 1, 1, 1 } }; |
|
0 |
0 |
1 |
1 |
2 | |
0 |
1 |
2 |
2 |
3 | |
0 |
1 |
3 |
2 |
3 | |
0 |
1 |
2 |
1 |
2 | |
0 |
0 |
1 |
1 |
1 |
|
The Approach!
There are many advanced algorithms to generate terrains; I am using a very simple solution for the purpose of this project.
In a nutshell, I used a 32 x 32 grayscale bitmap to represent a height-field that is used to generate the terrain. The terrain itself is divided into a grid of height values, the result of which is a mesh representing the terrain in the scene.
We create a grid of vertices that are spaced evenly apart but have varying heights, based on the height-field data. The color value of each bit is used to determine the height value of each grid location; in this case, for a 24-bit grayscale bitmap, the values for the color range from 0 to 255.
Once the bitmap has been read and the values loaded in memory, we have the data needed to represent the terrain. We also use a variable called a MAP_SCALE to allow us to scale the map up or down. This is a scale factor; we use this to set the distance between each height vertex. This allows us to increase or decrease the size of the terrain.
When we actually assign the vertex coordinates for each grid location, we need to apply the MAP_SCALE factor, which is multiplying it with the grid location index based on the coordinate element, i.e.:
Terrain[X][Z][0] = Float(X)*MAP_SCALE;
Terrain[X][Z][1] = (float) imageData[(Z*MAP_SCALE+X)*3];
Terrain[X][Z][2] = Float(Z)*MAP_SCALE;
The terrain map is represented in a grid of height values, which is internally stored in a 2D array of vertex coordinates. It extends along the X and Z-axis, with the Y-Axis representing the terrain height.
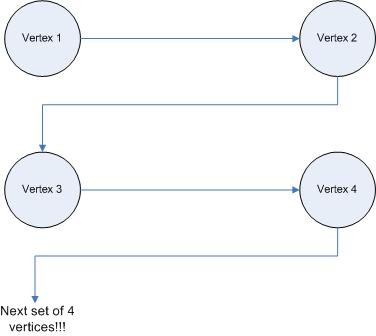
To render the terrain map, we use GL_TRIANGLE_STRIP for each row of grid values along the Z-axis. To render the terrain correctly, we need to specify the point in a specific order.
This requires us to start at the end of the row and move along the positive X-axis by drawing the vertices in a Z pattern:
The following is a sample of the bitmap used to generate the height-field:

The following is the output of the generated terrain based on the bitmap file:
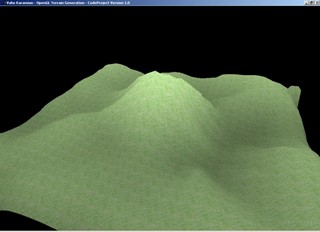
Using the Code
I will only list the code that deals with the terrain generation here. There is more code in the project that you can look at. It is well documented, so you shouldn't have any problems. The solution was compiled using MS Visual Studio 2003, so you should be able to compile and run it easily. You will need to have the OpenGL libraries and DLL, which I will also provide as a download option just in case you do not have them. Make life a little easier so you do not have to search for them online.
So the majority of the code is for preparing the windows to render the scene properly. As you can see below, the code for generating and rendering the terrain is very short. To give an overview, the first thing that happens is for the windows to get created, and then we initialize OpenGL, and read in the BMP file and assign it to the 2D array we discussed above. Then, the texture is applied to the surface of the mesh, and the scene rendered to the screen.
Without further ado, the following listing is the the portion of the code which initializes and generates the terrain:
.
.
.
void InitializeTerrain()
{
for (int z = 0; z < MAP_Z; z++)
{
for (int x = 0; x < MAP_X; x++)
{
terrain[x][z][0] = float(x)*MAP_SCALE;
terrain[x][z][1] = (float)imageData[(z*MAP_Z+x)*3];
terrain[x][z][2] = -float(z)*MAP_SCALE;
}
}
}
.
.
.
The code above is the implementation of what we discussed about applying MAP_SCALE, which allows us to scale the terrain to our likings. So, it basically assigns the vertex coordinates for each grid location, the MAP_SCALE factor, which is multiplying it with the grid location index based on the coordinate element. It extends along the X and Z-axis, with the Y-Axis representing the terrain height.
The function is called after the bitmap has been loaded into the memory from the Initialize() function.
.
.
.
void Render()
{
radians = float(PI*(angle-90.0f)/180.0f);
cameraX = lookX + sin(radians)*mouseY;
cameraZ = lookZ + cos(radians)*mouseY;
cameraY = lookY + mouseY / 2.0f;
lookX = (MAP_X*MAP_SCALE)/2.0f;
lookY = 150.0f;
lookZ = -(MAP_Z*MAP_SCALE)/2.0f;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
gluLookAt(cameraX, cameraY, cameraZ,
lookX, lookY, lookZ, 0.0, 1.0, 0.0);
glBindTexture(GL_TEXTURE_2D, land);
for (int z = 0; z < MAP_Z-1; z++)
{
glBegin(GL_TRIANGLE_STRIP);
for (int x = 0; x < MAP_X-1; x++)
{
glColor3f(terrain[x][z][1]/255.0f,
terrain[x][z][1]/255.0f,
terrain[x][z][1]/255.0f);
glTexCoord2f(0.0f, 0.0f);
glVertex3f(terrain[x][z][0],
terrain[x][z][1], terrain[x][z][2]);
glTexCoord2f(1.0f, 0.0f);
glColor3f(terrain[x+1][z][1]/255.0f,
terrain[x+1][z][1]/255.0f,
terrain[x+1][z][1]/255.0f);
glVertex3f(terrain[x+1][z][0], terrain[x+1][z][1],
terrain[x+1][z][2]);
glTexCoord2f(0.0f, 1.0f);
glColor3f(terrain[x][z+1][1]/255.0f,
terrain[x][z+1][1]/255.0f,
terrain[x][z+1][1]/255.0f);
glVertex3f(terrain[x][z+1][0], terrain[x][z+1][1],
terrain[x][z+1][2]);
glColor3f(terrain[x+1][z+1][1]/255.0f,
terrain[x+1][z+1][1]/255.0f,
terrain[x+1][z+1][1]/255.0f);
glTexCoord2f(1.0f, 1.0f);
glVertex3f(terrain[x+1][z+1][0],
terrain[x+1][z+1][1],
terrain[x+1][z+1][2]);
}
glEnd();
}
glEnable(GL_BLEND);
glDepthMask(GL_FALSE);
glBlendFunc(GL_SRC_ALPHA, GL_ONE);
glDepthMask(GL_TRUE);
glDisable(GL_BLEND);
glFlush();
SwapBuffers(g_HDC);
}
.
.
.
The first thing you see in the Render() function is the conversion of the angle into radians, by using the formula: radians = float(PI*(angle-90.0f)/180.0f);. This makes it easier to compute the cameraX, cameraY, and cameraZ positions using the sin() and cos() functions.
The next block of code sets the look-at coordinates of the camera at the center of the terrain. Then, we clear the screen and depth buffer using glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);. We set the camera position based on the camera (X, Y, Z) values and the look-at we computed.
We then bind the texture using the glBindTexture(GL_TEXTURE_2D, texture); function. This tells OpenGL that we are going to use that particular texture to apply to our surfaces that will be drawn.
So far, all the code was just to setup the camera position and bind the texture, the next block of code is what actually draws the terrain and applies the texture to the surface. We have two for loops which go through the 2D array we have created that stores the terrain data, and as we discussed earlier, we process four vertices at a time. In the process, we calculate the grayscale shade color, we set the texture, and then we draw the vertex.
That is pretty much all you need to do to generate a terrain, given a 24-bit bitmap file.
Points of Interest
If you are reading this, you most likely are interested in computer graphics and want to learn more about the techniques available to do really cool stuff. Computer graphics can be very complex in theory, but thanks to libraries such as OpenGL, the implementation of complex models/scenes can be done easily. Upon writing this article, I got the latest issue of Dr. Dobb's Journal (June 2006, Issue No. 385), and to my surprise, there is an article about OpenGL and Mobile Devices. It is under the name of OpenGL ES and it is a subset of OpenGL 1.3. That will make it possible to do real time 3D graphics on hand-held devices. Imagine the kind of nice looking applications/games that can be developed for your PDA or cell phones! Not all the functionality is available due to the limitations of the hand-held hardware. But I assume, in the near term future, you will be able to create as fascinating graphics on the handhelds as you can on your regular desktop machines.
On another note, I am going to start working on a new article which will describe the LoadBitmapFile(char *filename, BITMAPINFOHEADER *bitmapInfoHeader) function. I am looking forward to hearing your comments and input, for future articles.
