Introduction
This article describes how to solve a logic problem using the AI Search technique.
So what is the problem that are trying to solve
The problem is specified like this. On one side of a river, there are three missionaries and three cannibals. There is a boat which can be used to transfer people from one side of the river to the other.
No more than two people can fit in the boat and it must have at least one person in it during any transfer. The problem is to find the shortest sequence of transfers which gets all six people from one side to the other without ever creating a situation where missionaries outnumber cannibals on either side of the river. (The idea being that if this happens, the missionaries will then be able to corrupt the cannibals by 'converting' them.) To solve this problem satisfactorily, your program must explicitly identify all of the optimal (i.e., shortest) solutions to the problem.
How does an AI search algorithm work
Well, there are different varieties of search which can all be used, such as breadth first, depth first, or iterative deepening. Each of these different search methods has different properties such as whether a result is guaranteed, and how much time and space is needed to carry out a search.
This article uses breadth first search, as this search method is guaranteed to find a solution state.
Search is generally concerned with looking for a solution, or solutions in a search space of individual search states. Typically, a search space is a list or some sort of collection which contains each of the states that is to be checked to see if it is a solution state.
A breadth first search algorithm
A breath first search relies upon the basic search principles mentioned above. What is of specific interest, is how the breadth first search actually goes about looking for a solution state.
To illustrate this, consider the following diagram, where each of the ovals is an individual state:
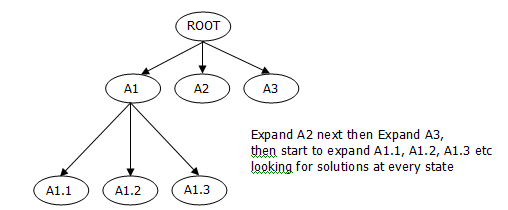
It can be seen from the diagram above that there are a number of states, but how did the search choose which ones to look at for a given solution?
With a breadth first search, each state at a given layer is expanded before moving to the next layer of states. In the diagram above, it can be seen that the root state was expanded to find the states A1, A2, and A3. There were no more states at this level, so A1 was picked and expanded, which yielded A1.1 -> A1.3. However, A2 and A3 must also be expanded before looking at these new states A1.1 -> A1.3, so A2 and A3 will be expanded next. If there are no more states at the current level to expand, the first node from the next level is expanded, this carries on until a solution (or solutions) is found. This is the basis of a breadth first search.
So how does this translate into an algorithm
The following algorithm illustrates how a breadth first search should function when looking for a single solution.
- Create a variable called SearchAgenda (say) and set it to the initial state (Root, from our example).
- Until a goal state (Solution) is found or SearchAgenda is empty, do:
- Remove the first element from SearchAgenda and call it CurrState. If SearchAgenda is empty, quit.
- For each way that each rule can match the state described in CurrState, do:
- Apply the rule to generate new state(s), these are called Successor states.
- If the new state is a goal state (Solution), quit and return this state.
- Otherwise, add the new state to the end of the SearchAgenda.
This is the basis of the algorithm. But there are some considerations, which are fairly important to any AI search technique. These are explained below.
Finding successor states
This is a fundamental part of any search algorithm, and is really the key to having a successful search algorithm. For the Missionaries and Cannibals problem, we could consider the following diagram.

From the figure above, we can see that several of the states are invalid, so have been pruned (discarded) from the search tree. This means these states will not have successor states generated.
Determining if the new state is a goal
For the Missionaries and Cannibals problem, this is simply having all three missionaries and all three cannibals on the opposite side of the river.
Using the code
The demo project attached actually contains a Visual Studio 2005 solution, with the following three classes:
Program
Is the main entry point into the CannMissApp application. Essentially, all this class does is call the getSolutionStates method of the SolutionProvider, and then print the solutions (if there are any):
.....
.....
SolutionProvider S = new SolutionProvider();
ArrayList Solution = S.getSolutionStates(new State("Root", 3, 3, false,1),
new State("Goal", 0, 0, true,999999));
printSolutions(Solution);
....
....
private static void printSolutions(ArrayList Solution)
{
if (Solution.Count == 0)
{
Console.WriteLine("\n\nNO SOLUTIONS HAVE BEEN FOUND\r\n");
}
else
{
int Solfound = 1;
for (int i = 0; i < Solution.Count; i++)
{
State s = (State)Solution[i];
Console.WriteLine("=====FOUND SOLUTION [" +
Solfound++ + "]=====\r\n");
Console.WriteLine("This solution was found at level [" +
s.getStateLevel() + "]\r\n");
s.Print();
Console.WriteLine("\r\n");
}
}
}
SolutionProvider
Provides solutions to the "Cannibals and Missionaries" search problem:
using System;
using System.Collections.Generic;
using System.Collections;
using System.Text;
namespace MissCanApp
{
#region SolutionProvider CLASS
class SolutionProvider
{
private int CURRENT_ROOT_STATE = 0;
private ArrayList searchAgenda = new ArrayList();
public SolutionProvider()
{
}
private void addStateToAgenda(String StateName,State parent,
int nMiss, int nCan)
{
int BoatDirection = parent.Side ? 1 : -1;
String newStateName = parent.getStateName() + StateName;
State newState = new State(newStateName,
parent.nMiss + nMiss * BoatDirection,
parent.nCan + nCan * BoatDirection,
!parent.Side,
parent, parent.getStateLevel() + 1);
addStateToAgenda(newState);
}
private void addStateToAgenda(State newState)
{
if (newState.InvalidState())
return;
searchAgenda.Add(newState);
}
public ArrayList getSolutionStates(State StartState, State EndState)
{
int optimalSolfoundAtLevel = 0;
bool allOptimalSolutionsFound = false;
bool foundFirstSolution = false;
ArrayList Solutions = new ArrayList();
addStateToAgenda(StartState);
while (searchAgenda.Count > 0 && !allOptimalSolutionsFound) {
State CurState = (State)searchAgenda[CURRENT_ROOT_STATE];
searchAgenda.RemoveAt(CURRENT_ROOT_STATE);
if (CurState.Equals(EndState)) {
if (foundFirstSolution) {
if (CurState.getStateLevel() <= optimalSolfoundAtLevel) {
Solutions.Add(CurState);
}
else {
allOptimalSolutionsFound =true;
}
}
else {
foundFirstSolution=true;
optimalSolfoundAtLevel = CurState.getStateLevel();
Solutions.Add(CurState);
}
}
else {
generateSucessors(CurState);
}
}
return Solutions;
}
private void generateSucessors(State CurState) {
int nCan, nMiss =0;
int stateName =1;
for (int i = 0; i <= Program.boatsize; i++)
{
for (int j = 0; j <= Program.boatsize; j++)
{
if (i==0 && j ==0)
continue;
if (i + j > Program.boatsize)
break;
nMiss = i;
nCan = j;
addStateToAgenda("_" + stateName++, CurState, nMiss, nCan);
}
}
}
}
#endregion
}
State
Is a representation of a node with the Search Agenda. Each State holds various bits of data which help to model a specific state, such as number of missionaries, number of cannibals, the side the boat is on etc.
using System;
using System.Collections.Generic;
using System.Text;
namespace MissCanApp
{
#region State CLASS
class State
{
public int nMiss, nCan;
public bool Side;
private int NumOfEachAtStart = 3;
private String Name;
private State PrevState;
private int stateLevel = 0;
public State(String Name, int nMiss, int nCan, bool Side,
int stateLevel) : this(Name, nMiss, nCan,
Side, null, stateLevel)
{
}
public State(String Name, int nMiss, int nCan, bool Side,
State PrevState, int stateLevel)
{
this.Name = Name;
this.nMiss = nMiss;
this.nCan = nCan;
this.Side = Side;
this.PrevState = PrevState;
this.stateLevel = stateLevel;
}
public int getStateLevel()
{
return this.stateLevel;
}
public String getStateName()
{
return this.Name;
}
public void Print()
{
if (PrevState != null) {
PrevState.Print();
}
String WhatSide = Side ? " BOAT RIGHT->" : "<-BOAT LEFT ";
Console.WriteLine(nMiss + "M/" + nCan + "C " + WhatSide + " " +
(NumOfEachAtStart - nMiss) + "M/" +
(NumOfEachAtStart - nCan) + "C");
}
public bool Equals(State StateToCheck)
{
return (nMiss == StateToCheck.nMiss &&
nCan == StateToCheck.nCan &&
Side == StateToCheck.Side);
}
public bool InvalidState()
{
int PersonType1 = 0;
int PersonType2 = 0;
if (Program.CanOutnumberMiss)
{
PersonType1 = nCan;
PersonType2 = nMiss;
}
else
{
PersonType1 = nMiss;
PersonType2 = nCan;
}
if (nMiss < 0 || nCan < 0 ||
nMiss > NumOfEachAtStart ||
nCan > NumOfEachAtStart)
return true;
if (PersonType1 < PersonType2 && PersonType1 > 0)
return true;
if ( (NumOfEachAtStart - PersonType1 <
NumOfEachAtStart - PersonType2) &&
(NumOfEachAtStart - PersonType1 > 0))
return true;
return false;
}
}
#endregion
}
The results
When run, the application will print all valid solutions that were found. It will find more than one.
The results should look something like the following:

Points of Interest
I hope this article is of interest to someone.
History
