Abstract
Starting with a common algorithm to generate all permutations of a string, I show the typical easy procedural version and then an object-oriented version. Noting that the algorithm produces all permutations before returning to the caller, I then show two iterator-style versions that let the caller control the generation of the permutations. One of them is the "inside-out" version, and the other uses a simple coroutine mechanism using a thread. That version turns out to not support stopping the iteration before it is done, so I correct that.
The downloadable code includes these program variations. The programming language used throughout is Java, but there is also an example in C# and an example in Haskell, for variety.
Contents
Introduction
A classic interview coding question is—or at least used to be—to write a program to generate all the permutations of a string.
I used to like to get it because it had a simple and elegant recursive solution that was easy to right the first time, when writing it on the whiteboard. And coming up with a good recursive solution in an interview used to impress interviewers, especially if you explained it nicely in a "mathematical induction" sort of way.
Recently I had two additional thoughts about that easy solution. The first was that recursive solutions were sort of the epitome of procedural programming, but what would be the object-oriented variant, and would it be as easy to write it correctly at the whiteboard?
The second thought was a bit more interesting: suppose you actually needed a permutation generator in your program (I never have), then you probably would not want the recursive solution anyway, which would generate all permutations—and process them—before returning to the caller. Instead, you'd want a demand-oriented, that is, iterator-style, solution that you could pull solutions out of when you wanted to. That sort of solution would be more difficult to express in a procedural language, and you couldn't easily change a recursive solution into a demand-oriented solution, but the object-oriented solution might be easier to adapt. And could you still do it at the whiteboard?
What follows is a simple exploration of these questions using my least favorite object-oriented programming language, Java. (Not my least favorite language that you can do object-oriented programming in: that would be Perl.) It is my least favorite because, due to its history, it is a very simple language that, though it is truly object-oriented, doesn't really have the syntax to be really expressive, thus your code becomes quite verbose. But nevertheless, it is the ubiquitous teaching language these days, and is lingua franca for this kind of discussion.
Procedural permutations: The easy recursive solution
(If you already know the easy recursive way to generate permutations, please skip ahead to the object-oriented approach here.)
The first thing I would say (at the whiteboard) is that I'd want to abstract away what to actually do with the generated permutations. So I'd quickly define a standard "action" interface:
public interface Action {
void next(String s);
}
And then, a class that implements Action and I'd write the main procedure first. Permute is going to be the procedure that generates the permutations:
public final class RecursivePermute {
public static void main(String... args) {
final String p = args.length > 0 && args[0].length() < 0 ? args[0] : "abcd";
Permute(new Action() {
public void next(String s) {
System.out.println(s);
}
}, p);
}
...
At any given recursive level, the procedure takes in the current permutation of and a "tail" of characters yet to be included in the permutation strings. It takes the first character of that tail and creates all the variants of the current permutation with that character interposed—including before the current string and after it. It does this one-at-a-time, of course, calling itself recursively on the remainder of the tail, each time, so that all the permutations at the next level will be generated.
The actual recursive procedure that generates the permutations is going to take an extra argument beyond the string to be permuted: the tail. And we're going to start at the outermost level with a 0-length string, then the next inner recursive level will have a 1-length string, then the next level will be dealing with length 2 strings, etc.
Because we have to pass the tail in our recursion—and because Java doesn't have default arguments—we're actually going to have to write two procedures: the one the user will call, and a 2-argument helper.
public static void Permute(Action a, String p) {
if (p.length() > 0) {
Permute(a, p, "");
}
}
private static void Permute(Action a, String tail, String p) {
assert a != null && p != null && tail != null && tail.length() > 0;
for (int i = 0; i < p.length()+1; i++) {
String nextp = p.substring(0, i) + tail.charAt(0) + p.substring(i);
if (tail.length() > 1) {
Permute(a, nextp, tail.substring(1));
} else {
a.next(nextp);
}
}
}
And that's the recursive solution, in the last box.
But really, you can see already that for a complete working solution, Java requires that all procedures really be methods in some class, and doesn't have some of the syntactic sugar that other languages have to shorten the code (such as default parameters) so it is pretty verbose. I don't think I'd require all the boilerplate of an interviewee, myself, as long as I heard some kind of hand-waving explanation about how it would need to have a class fitted around it.
(Actually, this example would be slightly shorter if I had skipped the Action business and just did a System.out.println() at the end of the recursion. But I'll want the action abstraction later, when I turn this into a "pull-style" procedure.)
Functional permutations: The one-liner
Oh, I guess you might think I was just whinging about how much extra typing I needed to do in Java. Just for fun, what would this exact algorithm, as a fully runnable program, look like in Haskell?
import Data.List
permute [] = [[]]
permute (x:xs) = [ pre ++ [x] ++ post | ys <- permute xs,
let ss = splits ys, (pre,post) <- ss ] where
splits a = zip (inits a) (tails a)
Oh. That's totally executable code. And it isn't even the best you can do. How about this alternative, given by Sebastian Sylvan:
perms xs = [ x:ps | x <- xs, ps <- perms (xs\\[x]) ]
Well, I'm not going to explain either of these programs. The first one, the one I wrote, took me about 5 minutes to write and fully test using the Haskell Platform and it only took that long because I wasn't sure which module to find the functions inits and tails in.
Functional programming lets you express algorithms very concisely, and once you are used to it, very clearly. But it requires a different mindset than procedural or object-oriented programming. I encourage you to look into it; you can pick it up from tutorials and papers on the web, or via books, but it does require some study in order to become effective. But it's worth it! Once you can look at things in the functional frame, you get great benefits in thinking clearly even when using procedural or object-oriented languages.
Object-oriented permutations: A chain of permutation steps
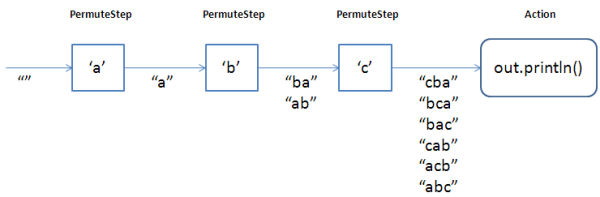
So what does an object-oriented version of this look like? Instead of a recursive procedure, where each level of recursion passes permuted strings down to the next level, which interposes one character at each location, we'll have a chain of objects, where each object passes permuted strings on to the next object in the chain, which interposes one character at each location.
There will be one object in the chain for each character of the initial string to permute; they'll all be of one class, which implements Action, which is what will chain them together. And there will be a final object in the chain, which is the Action that the caller wants performed.
(The illustration at the top of this article shows how this chain of objects works.)
With that in mind, the code almost writes itself. The main method (and the Action interface) are identical to what we had before so just writing the new code, we first create the class which acts as the links in the permutation chain. Each instance holds its own character to interpose, gets new strings to permute via its own next(), and passes on the interposed strings to the Action it is holding.
private static final class PermuteStep implements Action {
private final Action a;
private final char c;
private PermuteStep(char c, Action a) {
this.c = c;
this.a = a;
}
public void next(String s) {
for (int i = 0; i <= s.length(); i++) {
String n = s.substring(0, i) + c + s.substring(i, s.length());
a.next(n);
}
}
}
And with that, building the chain of permutation steps and then running it to generate all permutations is easy:
public static void Permute(Action a, String p) {
Action as = a;
for (char c : p.toCharArray()) {
as = new PermuteStep(c, as);
}
as.next("");
}
So it turns out that the object-oriented version is barely larger, and may even be simpler to understand. It's certainly a worthy contender for a simple whiteboard solution.
What is the performance of the object-oriented version compared to the recursive version?
First, it must be recognized that in most circumstances, it hardly matters. The code to generate a single permutation consists of a little more than a few string concatenations and a single procedure call, in both versions. Almost any practical use of a permutation generator will execute more code dealing with each permutation string than in generating it. Even the simple out.println(s) in this example executes far more code for each permutation than it cost to generate it.
But there might be examples where the cost to use each permutation is low, for example, if for some reason you're generating all permutations but immediately filtering away most of them with some kind of cheap test. In that case we may look into the cost of generating a single permutation.
For that, we find that there are only three real differences. First, the object-oriented solution creates a fixed number of objects to form the chain: one for each character in the initial string. The recursive implementation doesn't do this, but it does create the "tail" at each level and passes it on. In fact, it will end up creating far more strings than the object-oriented version, and typically, far more objects than the fixed number of permutation step objects created by the object-oriented version.
Second, the recursive implementation passes (at least) two arguments via the stack (ignoring the Action at the moment). In a procedural language those two strings would be the only arguments passed on the stack. The object-oriented version is passing only one string on the stack, but also has to pass the receiving object. Either way, it seems the stack usage is going to be very similar between the two approaches.
Finally, in either case, the strings or the objects are going to be accessed indirectly via pointers, but the compiler or JITter will ensure that frequently used values (for example, the character to be interposed) are kept in machine registers for fast access.
I would guess (without measuring it) that the recursive implementation and the object-oriented version will be very similar in performance in the cost of generating permutations, if it actually matters.
Iterator-style: Generation of each permutation on demand
Now it's time to look at the generation of permutations "on demand", or iterator-style.
As I mentioned earlier, the flaw in the recursive-style of permutation generation is that it generates all permutations at once, before returning to the caller. That's one use case, but I think it would be more common to want permutations to be generated one-at-a-time on demand.
Object-oriented languages usually offer an abstraction for this, typically called an iterator. This is usually embodied as a small interface that, when implemented by a class, allows instances of that class to be used in iterator contexts, for example, in a "for each" loop. The instance encapsulates the current state of the iteration.
Using an iterator is easy. But without language support for writing the implementation of the iterator, you might need to change algorithms, or else suffer the pain of turning your code "inside out". That is, you have to turn your generator into a state machine, and provide ways to return out of and then jump back into the middle of your algorithm.
In fact, this is exactly the kind of support that C# offers via iterator blocks and the yield return statement. Using these constructs an iterator can be written very simply and the compiler does the work of converting it to a state machine. (The details are actually intricate, and involve compiler generated classes and methods. There are plenty of articles on the web explaining how C# implements iterator blocks.)
Here is an example of how easy it is to turn our recursive algorithm into an iterator-style permutation generator in C#. Notice how both the immediate call to next and the recursive call to Permutations are inside of yield return statements which implement the coroutine mechanism. And also notice how the return type is of the interface IEnumerable<>—it is the combination of that return type plus the yield return statement that tells the compiler to turn this method into an iterator.
static IEnumerable<string> Permutations(string p, string tail)
{
Debug.Assert( tail.Length > 0 );
for (int i = 0; i < p.Length+1; i++)
{
string nextp = p.Substring( 0, i ) + tail[ 0 ] + p.Substring( i );
if (tail.Length > 1)
{
foreach (string s in Permutations(nextp, tail.Substring(1)))
{
yield return s;
}
}
else
{
yield return nextp;
}
}
}
And here is a C# main procedure that iterates over all permutations of a string, using the standard foreach statement:
static void Main( string[] args )
{
string p = args.Length > 1 ? args[ 0 ] : "abcd";
foreach (string s in Permutations("", p))
{
Console.Out.WriteLine("{1}", s);
}
}
Iterator-style: Generating permutations inside-out
Java doesn't have any nice way to have the compiler build coroutines for you, the way C# does. So we'll have to do it ourselves. Our first try will be to "turn" the permutation chain algorithm "inside-out".
In Java iterators implement the java.util.Iterator interface, which is generic in the type T that it iterates over. Iterator<T> has three methods: boolean hasNext(), T next(), and void remove(). hasNext and next are the real workers in an iterator (but already we see another Java annoyance: we have to implement remove even though we have no intention of using it—it has no meaning in the context of our iterator, applying mainly to collections).
For convenience, we'll also implement java.lang.Iterable, which is an interface used on a class instance to get an iterator, in some contexts, for example, in a for statement. Iterable only has a single method, iterator() which returns an iterator.
Anyway, what we're going to do is build the same chain of objects as before, one object in the chain for each character to be in the permutations. But the objects are different. First, instead of chaining on the Action interface, which "pushes" permuted strings down the chain, we'll chain on the Iterator interface, which "pulls" permutations up the chain.
Second, we'll end the chain not with the caller's Action, but with a special object that simply returns a zero-length string, and does that only once.
As you can see, this chain operates "backwards" with respect to the object-oriented chain we built earlier.
Let's start with the end of the chain. We need an object which will be an iterator, and which, when iterated upon, will return a single 0-length string. We'll start here because it is easiest, and will also show us the methods for the Iterator interface.
private static final class PermuteChainEnd implements
Iterator<String>,
Iterable<String> {
@Override
public Iterator<String> iterator() {
return this;
}
private boolean once = true;
@Override
public boolean hasNext() {
return once;
}
@Override
public String next() {
if (once) {
once = false;
return "";
} else {
throw new NoSuchElementException();
}
}
@Override
public void remove() {
throw new UnsupportedOperationException();
}
}
That's a pretty minimal iterator.
Now we'll do the ordinary PermuteStep that makes up the permutation chain. Remember, we're going to return only one interposed string at a time from the permuted string we got from farther back in the chain. So we need to remember what position we're at in the current permuted string.
Also, when we've reached the end of the current string and have no more positions left in it to interpose our character, we have to call the iterator from the next chain object to get the next string to interpose into.
We already have to split the string we're holding in order to fit the character in. So we'll keep those two splits, the prefix and suffix and use that as our state, to keep track of what we need to do next.
With a little thought, we can settle on the following invariant: if the suffix has no characters then we're done with the current string and it is time to get the next one from the next object in the chain. And, in that case, we immediately return as our current permutation the string returned with our character prepended to it. On the other hand, if the suffix has characters, then we shuffle the first character of suffix onto the end of the prefix, and return the concatenated prefix and character and suffix as our current permutation.
With that invariant in mind, we can see how to initialize our chain instance, and how to determine if there are any permutations left.
Here's the code. First, the boilerplate for the class and the interface Iterable. The state that we have to hold on to consists of four things: our character c, the next chain object, for which we have an iterator, a, and the strings which are the prefix and suffix of the current permutation we're working on.
private static final class PermuteStep implements
Iterator<String>,
Iterable<String> {
private final Iterator<String> a;
private final char c;
private String suff;
private String pre;
private PermuteStep(char c, Iterator<String> a) {
this.c = c;
this.a = a;
this.pre = "";
this.suff = "";
}
@Override
public Iterator<String> iterator() {
return this;
}
Based on the above invariant, we see that there are more permutations left if we still have characters in our suffix, or if there are none left, then there are more permutations left if the next object in the chain still has permutations to offer.
@Override
public boolean hasNext() {
return suff.length() > 0 || a.hasNext();
}
To actually return the next permutation we need to either shuffle a character from the suffix to the prefix, or get a new suffix from the next object in the chain.
@Override
public String next() {
if (suff.length() > 0) {
this.pre += this.suff.charAt(0);
this.suff = this.suff.substring(1);
} else {
this.pre = "";
this.suff = a.next();
}
return this.pre + this.c + this.suff;
}
Don't forget to provide an implementation for remove(), but I'm going to skip it here. That's all of the PermuteStep class, so it isn't too bad.
Now, we have to build the permutation chain. We'll do that in the class that contains both PermuteStep and PermuteChainEnd. It really isn't any different from the object-oriented solution above.
public static Iterable<String> Permute(String p) {
Iterable<String> a = new PermuteChainEnd();
for (char c : p.toCharArray()) {
a = new PermuteStep(c, a.iterator());
}
return a;
}
And finally, let's use this iterator-style permutation-generating chain. It's really quite simple: we use the construct that Java intends us to use with iterators: the for statement.
public static void main(String... args) {
final String p = args.length > 0 && args[0].length() < 0 ? args[0] : "abcd";
for (String s : Permute(p)) {
System.out.println(s);
}
}
Well, that's done. But, there was more code to write than you'd think, though it was more the tediousness of the iterator methods than anything else. The trickiest part was the representation of the iterator state in the class PermuteStep. I'm pretty sure I could get that right at the whiteboard, but then again, this is a pretty simple algorithm. What if we needed to turn something more complicated "inside-out"? Is there a different way to get an iterator-style algorithm from an object-oriented algorithm?
Iterator-style: Generating permutations via a thread
Yes, there is. And it seems like it will be simpler.
What we really want, as mentioned above, is a coroutine system, which Java lacks. But Java does have threads, so we can implement coroutines with threads. Even though such an implementation will be "heavier" than a true coroutine, it won't be too bad, and for some uses, won't be bad at all.
What we'll do is put the entire original object-oriented permutation generation chain into a thread (the procedural recursive routine would do just as well) and have it send its generated permutations to the main thread one at a time. The main thread will do whatever it wants to do and whenever it needs the next permutation, it will wait for it.
Java has a very nice class to do the transfer of an object from one thread to another, java.util.concurrent.Exchanger. The exchanger provides a synchronization point for two threads, which use it cooperatively. Each thread calls the exchanger's exchange() method, providing it with an object. The first thread to call exchange waits. When the second thread calls it the objects are exchanged and both threads continue—each has the object the other provided to the call.
We're going to only be using the exchanger in one direction: providing permuted strings from the permutation chain to the caller thread. So the calling thread will exchange a null instead of an object.
We're going to use the Iterator interface as before, for the demand-style permutation generator. This means that the last link in the chain will be an Action that exchanges the newly generated permutation with the calling thread. The calling thread will be the one with the iterator object. The iterator will create the permutation chain and start it running in a thread. Then, whenever it is called for the next object, it will use the exchanger to get it.
Now, a complication arises because of the interface Iterator. To use the iterator, first you call its hasNext method to see if there is a next item, then you call its next method to get the next item. (Also, you can call hasNext more than once before calling next and of course it can't "consume" the next item if you do that.) This means we're going to have to have a one-item lookahead cache. We'll fill it (if possible) on the hasNext call, and use it on the next call. (Of course, you don't actually have to call hasNext...—we have to account for that.)
Our new permutation generation class is an iterator (and an iterable), and because it will also be running the permutation chain it is also a runnable.
import java.util.Iterator;
import java.util.concurrent.Exchanger;
public final class CoPermute implements
Runnable,
Iterator<String>,
Iterable<String> {
private final Exchanger<String> exchanger = new Exchanger<String>();
There's our exchanger object, which will be shared between the calling thread (which is holding the iterator), and the permutation generating thread.
The class PermuteStep is exactly the same: that's the point here—there's no change to the object-oriented permutation generator, we're just wrapping it in a coroutine.
However, the end of the chain is different, since that's where we're going to synchronize with the main thread and pass the new permutation string to it.
private static class PermuteStart implements Action {
private final Exchanger<String> exchanger;
private PermuteStart(Exchanger<String> exchanger) {
this.exchanger = exchanger;
}
@Override
public void next(String s) {
try {
exchanger.exchange(s);
} catch (InterruptedException e) {
}
}
}
The only interesting line there is where we take the new permutation and pass it to the calling thread with exchanger.exchange(s). But we have to handle the exception InterruptedException which can be thrown by exchanger.exchange and is not a runtime exception.
We don't expect our thread to be interrupted, so we'll just eat that exception. But it is annoying to have to catch it just so our code will compile.
The next step is to start the permutation generator running. Building the permutation chain is just like before. To run it we'll start ourselves (remember, we're a Runnable), and in our run method, we'll start the generator. At the end, we'll take care of a detail: How will the iterator know there are no more permutation strings? The answer is: we'll exchange a null from the generator thread to the iterator thread, and that will be the signal.
private Action a;
private CoPermute(String s) {
a = new PermuteStart(exchanger);
for (char c : s.toCharArray()) {
a = new PermuteStep(c, a);
}
new Thread(this).start();
}
@Override
public void run() {
a.next("");
try {
exchanger.exchange(null);
} catch (InterruptedException e) {
}
}
That was pretty easy. Once again we had to eat an InterruptedException but otherwise the code is pretty clean.
Now, it is time to implement the iterator, which is receiving permutations from the generation thread. We've already discussed how we have to have a one-item lookahead, and here is where we implement it.
private String peek = null;
private boolean peeked = false;
private String lookAhead() {
if (!peeked) {
try {
peek = exchanger.exchange(null);
} catch (InterruptedException e) {
}
peeked = true;
}
return peek;
}
@Override
public Iterator<string /> iterator() {
return this;
}
@Override
public boolean hasNext() {
return lookAhead() != null;
}
@Override
public String next() {
String p = lookAhead();
peeked = false;
if (p == null) {
throw new NoSuchElementException();
}
return p;
}
(Don't forget to implement remove! And there's that darn InterruptedException yet again!)
It may seem a bit queer that the same class is being used as the iterator, and as the runner of the permutation generator. But there's no need to separate the functions into two different classes, and the functionality is evenly split between the implementation of the Iterator interface in the iterator thread, and the Runnable interface in the permutation generation thread.
At this point, we're done, and we can compare this implementation with both the object-oriented implementation, and the inside-out iterator implementation.
This version is an iterator-style version, meaning it produces permutations on demand, which we thought was more useful than the original permutation chain version which produces all of the permutations in a row before returning to the caller.
But as far as the complexity of the code goes, compared to the object-oriented implementation there's a lot more of it. The permutation generation algorithm is exactly the same. All the new code is there to communicate from the generation thread to the iterator thread, to create the generation thread, and to implement the iterator. Certainly we'd need code to implement the iterator, but it is more complex in this version. And comparing it to the inside-out iterator version we see that the original algorithm is unchanged—a big plus!—and all of the added complexity is isolated, where in the inside-out algorithm the complexity was added to the original algorithm (and if the task had been something more difficult than permutation generation, the "inside-out" state machine might have been very complex).
Still, all of that setup code for the thread and the inter-thread communication is a "one-time" cost, independent of the size and complexity of the algorithm that is producing the objects being iterated over. You can imagine that if that algorithm itself was more complex, this setup code would not be larger or more complicated at all, so its complexity and cost is fixed. We're beyond the stage where we can do this correctly at the whiteboard in an interview setting, but it isn't so bad as a homework assignment.
For the runtime cost, this version is definitely more expensive than either the object-oriented version or the inside-out iterator version. First of all, there's a thread to create and run. And second of all, each generated permutation requires two threads to synchronize, which itself is rather expensive.
These extra costs might not be significant if the algorithm encapsulated by the iterator (in the separate thread) is complex enough. But there are also other ways to amortize the cost. For example the cost of synchronization can be reduced by synchronizing less often. This can be done either by returning more than one object at each synchronization, or by using a queue to decouple the generation of permutations from the consumption, and thereby requiring fewer synchronizations (and fewer context switches). A java.util.concurrent.BlockingQueue might be just the thing to use.
Uh, a problem with our coroutine implementation?
So, now we're done? Not exactly... in fact, our iterator-style implementation, via a thread acting as a coroutine, has a major flaw.
What if we don't want to generate all the permutations? Perhaps we're just looking for the first one that satisfies a condition, then we break out of our loop.
Let's try it:
public static void BrokenPermute(Action a, String p) {
for (String s : new CoPermute("abcde")) {
a.next(s);
if (s.charAt(0) == 'e') {
break;
}
}
}
Compiles and runs fine. Wait a sec... it didn't terminate! In fact, if you add a out.println("exiting!") to the end of the main method, you see that the message gets printed but the program doesn't terminate!
And the reason is, the permutation generation thread has generated the next permutation and is waiting patiently in the exchanger for the iterator to pick it up. So the thread is still active (suspended, not running).
When control left the for loop, the iterator wasn't needed anymore. The main thread no longer has a reference to it. But it isn't garbage: it's run method still hasn't returned. It's stuck in the exchanger.
The for loop doesn't know to notify the thread it's no longer needed. It's almost as if it's waiting to be interrupted...
Oh. Maybe it does need to be interrupted! And maybe that's why InterruptedException isn't a runtime exception: the Java framework wants you to know that, more often than not, you have to plan for your threads to be interrupted, so that you exit them gracefully, when necessary.
So the first thing to know is that Java threads have a mechanism, the interrupt, which is what you use when you need a thread to gracefully exit. Calling a thread's interrupt method sets a flag which the thread itself can, and should, check from time to time. If the thread is suspended in some kind of Java synchronization mechanism such as wait, join, or sleep, then the JVM throws InterruptedException in that thread. Either way, you know it's time to exit.
The second thing to know is, that when the for loop exits early without exhausting the iterator, there's no way for it to "notify" the iterator that it isn't needed anymore. You might think that if they went to the trouble to define a method remove that is only rarely needed (if you're iterating through a collection and want to support removing items while you're iterating) then they might have gone ahead and defined a method done so that the for statement could tell the iterator it wasn't going to be used anymore, but no, that didn't happen.
So how are we going to notify the iterator it isn't needed anymore, so it can interrupt the permutation generation thread, and have it exit?
We're going to use the dreaded finalizer.
Note, please, that there's a lot of nasty stuff written about finalizers on the web. It is easy to find emails and postings that say that finalizers are evil, and programmers who are even thinking of using a finalizer should just shoot themselves in the head and thus improve the quality of programming in general. That's going overboard. Finalizers are a big ugly wart, sure, and they're easy to misuse (especially if you think they're the "opposite" of a constructor—and you can also find plenty of articles on the web that say just that too!), and they're never going to perform particularly well, but there are circumstances when you can use one safely, and need to. This is one of those circumstances.
The two main problems with finalizers are that you can't tell when they're going to run, and they may not run at all. This means they're generally useless for "cleaning up" any kind of resource external to the Java environment that you're holding on to. For example, you can't rely on a finalizer to flush data out to a file and make sure it is getting written to disk, before your program exits. It doesn't have to run. You can't rely on a finalizer to close a database connection when you're done using the object that is holding it, because it isn't going to be run right away, and long before it is run you might very well end up having too many objects holding too many open database connections and fail to create one you really need.
There are other problems with finalizers too. Most are largely associated with "self-resurrecting" objects. That is, you're in a finalizer of an object that is being garbage collected and instead of going away nicely you stick a reference to yourself in some non-garbage object. And thus keep yourself alive. In cases like this, I think, maybe those guys who want you to shoot yourself in the head are right. And another problem with finalizers is that, when you're in a finalizer, any object reference you're holding may be to objects which have already been garbage collected! That makes it hard to write a finalizer, to be sure.
But in this case, we're staying within the language, and we're only going to use the finalizer to interrupt our thread. Plus we know the thread we're talking to isn't already garbage collected because—well, because that's the problem. It's still waiting in an exchanger. So this use of a finalizer is safe and proper, and if you still feel like writing me a nastygram insulting my father's mother, don't bother, just kick your cat instead.
Iterator-style: Generating permutations via a thread, correctly
So, to continue the discussion from the previous section, we're going to fix the problem that we can't stop generating permutations until all have been generated. We're going to do this by adding a finalizer to the iterator so it can interrupt the permutation generation thread, and then we're going to change the permutation generation thread so that it checks to see if it has been interrupted.
The first thing we have to do is make sure that the iterator is a separate object from the thing that is running the permutation generator thread. There was no reason to do that before, so we didn't. But now, we definitely want the iterator to be garbage collected, and we know that the problem is that the thread is not being garbage collected, so we have to separate them.
The second thing we have to do is handle the exception InterruptedException. But we don't want to just handle it directly, because if we did, we'd have to "pipe it through" our permutation generation algorithm back to the thread runner, and our goal is to leave that untouched. Instead, we're going to declare our own runtime exception and throw that in place of the InterruptedException we got. As a runtime exception we can catch it at a higher level (in the call tree) without having to declare it on every method along the way.
That pretty much explains it, so now I'll supply the code without further comment.
First, the containing class, and the exception class, REInterruptedException, we're going to use to communicate the shutdown of the permutation chain; unlike the native InterruptedException, this one is a runtime exception which needn't be declared or handled by the algorithm itself.
package com.bakinsbits.interview;
import java.util.Iterator;
import java.util.concurrent.Exchanger;
public final class InterruptableCoPermute implements
Iterable<String> {
private static class REInterruptedException extends RuntimeException {
public REInterruptedException(Throwable cause) {
super(cause);
}
}
Now we have the end of the permutation chain, where the completed current permutation is exchanged with the iterator thread. Same as earlier, except it translates the exception on an interrupt, as explained earlier.
private static class PermuteStart implements Action {
private final Exchanger<String> exchanger;
private PermuteStart(Exchanger<String> exchanger) {
this.exchanger = exchanger;
}
@Override
public void next(String s) {
try {
exchanger.exchange(s);
} catch (InterruptedException e) {
throw new REInterruptedException(e);
}
}
}
Here's the PermuteStep class, exactly as before, unchanged by our conversion of this whole algorithm to ab iterator-style coroutine-based implementation.
private static class PermuteStep implements Action {
private final Action a;
private final char c;
private PermuteStep(char c, Action a) {
this.c = c;
this.a = a;
}
@Override
public void next(String s) {
for (int i = 0; i <= s.length(); i++) {
String n = s.substring(0, i) + c + s.substring(i, s.length());
a.next(n);
}
}
}
Time to introduce the constructor for the containing class. All it does is squirrel away the string-to-be-permuted so that it is available when the caller requests the iterator.
private final String stringToPermute;
private InterruptableCoPermute(String s) {
if (s == null) {
throw new NullPointerException("s");
}
stringToPermute = s;
}
Having seen the class that comprises the steps of the permutation chain, and the end of it, here's the class that implements the head of the chain. It is responsible for starting up the chain, and for eating the REInterruptedException so that the thread will terminate cleanly when it is no longer needed.
private static class InterruptableCoPermuteChainHead implements Runnable {
private Action a;
private final Exchanger<String> exchanger;
public InterruptableCoPermuteChainHead(Action a, Exchanger<String> exchanger) {
this.a = a;
this.exchanger = exchanger;
}
@Override
public void run() {
try {
a.next("");
exchanger.exchange(null);
} catch (InterruptedException e) {
} catch (REInterruptedException e) {
}
}
}
And now, the iterator class. Every time it is asked for the next item it is going to go to the exchanger to get it from the permutation thread chain. That's just as before. But this time, it has a finalizer. When this iterator is found to be garbage the finalizer will be called and all it does is interrupt the permutation thread. That's it, then this iterator vanishes.
private static class InterruptableCoPermuteIterator implements
Iterator<String> {
private final Thread chain;
private final Exchanger<String> exchanger;
private String peek = null;
private boolean peeked = false;
public InterruptableCoPermuteIterator(Thread chain, Exchanger<String> exchanger) {
this.chain = chain;
this.exchanger = exchanger;
}
@Override
protected void finalize() {
chain.interrupt();
}
private String lookAhead() {
if (!peeked) {
try {
peek = exchanger.exchange(null);
} catch (InterruptedException e) {
throw new REInterruptedException(e);
}
peeked = true;
}
return peek;
}
@Override
public boolean hasNext() {
return lookAhead() != null;
}
@Override
public String next() {
String p = lookAhead();
peeked = false;
resetLookAhead();
return p;
}
@Override
public void remove() {
throw new UnsupportedOperationException();
}
}
Here is the method iterator() which starts the whole thing going. It creates a permutation chain, puts it in a separate thread, creates an iterator instance, and hooks everything together.
@Override
public Iterator<String> iterator() {
final Exchanger<String> exchanger = new Exchanger<String>();
Action a = new PermuteStart(exchanger);
for (char c : stringToPermute.toCharArray()) {
a = new PermuteStep(c, a);
}
Thread chain = new Thread(new InterruptableCoPermuteChainHead(a, exchanger));
chain.setDaemon(true);
chain.start();
return new InterruptableCoPermuteIterator(chain, exchanger);
}
And the main program to test the whole thing:
public static void main(String... args) {
final String p = args.length >= 1 && args[0].length() > 0 ? args[0] : "abcd";
Permute(new Action() {
public void next(String s) {
System.out.println(s);
}
}, p);
System.out.println("");
BrokenPermute(new Action() {
public void next(String s) {
System.out.println(s);
}
}, p);
}
public static void Permute(Action a, String p) {
if (a == null) {
throw new NullPointerException("a");
} else if (p == null) {
throw new NullPointerException("p");
}
for (String s : new InterruptableCoPermute(p)) {
a.next(s);
}
}
public static void BrokenPermute(Action a, String p) {
if (a == null) {
throw new NullPointerException("a");
} else if (p == null) {
throw new NullPointerException("p");
}
System.out.println("BrokenPermute iterating with for statement");
for (String s : new InterruptableCoPermute("abcde")) {
a.next(s);
if (s.charAt(0) == 'e') {
break;
}
}
}
}
This program exits! Unlike the previous version. But—here's an important detail—it exits only because of the call to setDaemon() when creating the permutation chain thread, in the method iterator() above.
The specification of the Java VM says that there are two kinds of threads: daemon threads, and non-daemon threads, and that the VM continues to run until all the non-daemon threads that have started have exited. The intent is that threads doing useful work keep the VM alive; those are the non-daemon threads. The other threads aren't doing useful work, most of them are just waiting for some synchronization to happen. They're worker threads without work to do, or they're waiting for some network input that may never happen, or whatever. In our case, the permutation chain thread isn't doing useful work most of the time. Most of the time it is just sitting around in the exchanger waiting to get rid of its last permutation. And if nobody is going to call it, because the main thread is going to exit, then it has no reason to exist. So, we turn it into a daemon by calling setDaemon and that way we can exit the program whether or not a garbage collection has picked up and destroyed the iterator that is holding onto the thread.
I might as well note here that though this solution works, and, as you see, can be fairly encapsulated, it still doesn't have the best performance. On the first garbage collection run after the iterator becomes garbage the finalizer will run and interrupt the permutation generation thread. The permutation generation thread will exit and it and the entire permutation chain will become garbage. But none of it will be picked up until the next garbage collection run. We just have to live with it.
Summary
In this tutorial I described an object-oriented way to generate permutations of a string. The problem isn't really that complex, but what I thought was interesting about it is that the object-oriented pipeline I created was just as simple to write and describe as the recursive solution; perhaps some people might even find it easier to understand. And though I'm sure this kind of solution isn't unique to me, I personally haven't run across it before; certainly never in an interview situation. For all the focus on object-oriented programming for the last 20 years, it seems that the standard procedural solutions come first to many programmer's minds.
Also, I pointed out that the original solution(s) which generate all permutations at once before returning to the caller don't actually fit the object-oriented model that well. Iterators are much more the thing to use. So I showed two ways to translate the basic algorithm to an iterator model. Turning the algorithm "inside out" wasn't so bad for this simple permutation scheme, but would be for a more complex algorithm. Turning the algorithm into a coroutine had the advantage that it didn't change the algorithm at all, so it still worked fine. But it did require a lot of code to arrange it and also has a runtime cost. The choice is yours.
Article revision history
- March 23, 2011: Original article.
