A Variable-based String Parser

• Download source files - 5.3 KB
• Download demo project - 38.3 KB

Introduction

Someone may call this a tokenizer rather than a parser. However, this is not just another string tokenizer. Actually the string tokenizer is one part of this work hence this can be used as a tokenizer if needed. However, the interesting part lies in the use of variables for parsing (you can control the attributes - such as length, possible strings, etc. of these variables!). In order to give a quick picture of the usage of this, I list three cases where this can be used. First one is simple whereas the second and third are more advanced.

1. Find all the words in a dictionary that are prefixed by "ad" and are post fixed by "y".
2. Find all occurrences (phrases) in a text, in the form "in <any word> of <one or two words> this" along with the two words that precede and succeed the phrase.
3. Find all the words in a dictionary in the form "<any no of characters> <one character, say X> <two or more characters> <X> (again)"

The concept in this is unifying a given string (may be a single word, number pattern or a whole text) with a given template consisting of variables and strings.

Example template is : aa+X+Y+b+Y+X where the variables are denoted in uppercase letters (X and Y in this). Constraints can be set such as "Variable X should have a length between 2 and 5", "Variable Y can be unified with only one of the strings in the set {ab,b,ca}".

Background

I am developing a part of speech tagger for Sinhala which is my native language. In Sinhala there is a strong connection between the prefix and postfix of a word and its part of speech tag (noun, verb, etc). However, there are no exact rules that manifest these connections and they are all probabilistic like in most other languages. I wanted to break the words in a dictionary according to various templates and try to explore the links between those templates and the part of speech tag of the word. The answer was to develop a tool to unify a given string with a given template which obviously consists of a sequence of variables and constants (strings).

I tried to make this tool as generic as possible so that it can be used in a totally different context. Later I used this for sentence parsing (rather than word parsing as in the original requirement) to explore word patterns in a sentence.

Unit of the String

I used "a string" rather than a character as the unit of the string so that it will be more generic. So the input string is a sequence of sub strings (a string list - CStrList class encapsulates this). If someone needs to use character as the unit (as is more common when the string to be unified is a word) he can use single character strings (I used CStrings).

Input and Output of the program

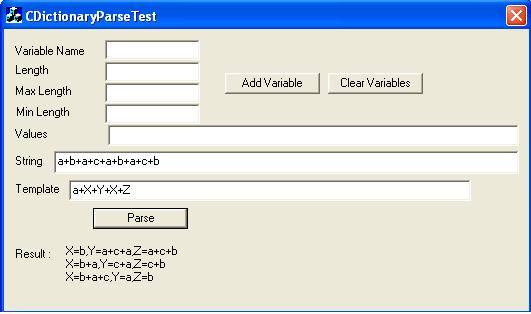
Inputs are the string (string list - more specifically) to be parsed and the template with which it should be unified. Output is a list of solutions where each solution has a unique combination of values for the variables. Let me show an example :

Input string : a+b+d+c+d+ab+b+d+c+b+aa

Template : a+X+d+Y+X+Z

where X, Y & Z are variables.

There will be three solutions :
1. {X = b, Y = c+d+ab, Z = d+c+b+aa}
2. {X = b, Y = c+d+ab+b+d+c, Z = aa}
3. {X = b+d+c, Y = ab, Z = b+aa}

We can reduce these number of solutions to tackle a more specific case by specifying constraints on variables.

Variables

A variable (which is encapsulated in the class CVariable) stands for a list of string units. Length of the variable is the number of string units it contain.

Properties of a variable are:

1. Length
2. Minimum length
3. Maximum length
4. Possible Strings (set of values - string lists - this variable can be unified with)

Setting these properties is optional. The user may leave behind any of them unset. For an example, if the possible strings list is empty for a given variable, the program assumes that the variable can be unified with any string. One or more of the properties can be set to the required values when constraints are needed. However, there's a built-in constraint which cannot be changed - the variable length should be greater than zero i.e. no variable can be unified with an empty string.

Algorithm

Let me explain the algorithm using another example. Say the template given is "a+X+a+Y+X+b+Z+d"(where X, Y and Z are variables) and the string to be parsed is "a+b+a+c+a+b+b+c+b+c+d"

1. We look for constants in the beginning and in the end of the template. In this case there's the constant "a" in the beginning of the template and the constant "d" at the end. We see whether these constants can be found in the beginning and the end of the given string. If found, we remove them from both the string and the template. If this test fails, the unification can be terminated i.e. there are no solutions.

   After the first step, we have to unify the string "b+a+c+a+b+b+c+b+c" with the template "X+a+Y+X+b+Z"

2. Now search for the intermediate constants in the template. Here, we find "a" and "b". We locate them in the leftmost possible orientation in the string.
   plain

   X a Y+X b Z
   b a c+a b b+c+b+c

   From this orientation, we derive the solutions for the variables as {X = b, Y+X = c+a, Z = b+c+b+c}.

3. Now we solve for this set of equations treating them like simultaneous equations. From the second equation (Y+X = c+a), we can derive only one breakdown i.e. Y=c & X=a because the minimum length of a variable is 1. However, X=a contradicts with X=b (first equation). Therefore this solution cannot be accepted.
4. Next step is moving the right-most constant (b here) into the next possible leftmost position. The orientation will look like following:
   plain

   X a Y+X b Z
   b a c+a+b b c+b+c

   The solution set is {X = b, Y+X = c+a+b, Z = c+b+c}

5. Solve the equations. From the second equation, there are two possible breakdowns.
   1. Y = c & X = a+b
   2. Y = c+a & X = b

   Breakdown (i) contradicts with the first equation. However, breakdown (ii) is a valid solution. The derived solution is {X = b, Y = c+a, Z = c+b+c}. We add this solution to our solution set.

6. Next, move the constant which is immediately left to the constant we were moving in the previous step. Moving rule is the same.
   plain

   X a Y+X b Z
   b+a+c a b b c+b+c

Derive the possible solutions and add the correct solutions to the solution set.

These are the first few steps of the algorithm. By now, you might have a rough idea about how it works. Now I'll describe the complete algorithm in a more formal way.

• First, remove the prefixing and suffixing constants (if any) in the template from both the string and the template.
• Position the remaining constants in the template (constants that are located between variables) in the leftmost possible orientation.
• After this, move one constant (towards right) at each step. The moving rule is : Move the leftmost possible constant to its next leftmost position. At each unique combination of constant positions, derive the possible solutions and add the correct solutions to the solution set. The procedure ends when no movement of constants are possible (i.e. when the constants are in their rightmost possible orientation.)

Using the code

Using the code is not difficult at all. You do not need to understand the algorithm to use the code. I'll explain all the steps needed to use it in your application.

1. Include "Parser.h" file.
2. Make an object of the class CParser.
   C++

   CParser m_Parser;

3. Add variables to the parser object.
   C++

   // create variable
   CVariable* pVar = new CVariable;
   
   pVar->s_Name = "X"; 
   pVar->i_MinLength = 2; 
   pVar->i_MaxLength = 5;
   // add possible strings
   // we add two possible strings (a+b  and  c)
   CStrList oStrList;
   oStrList.push_back("a");
   oStrList.push_back("b");
   pVar->lst_PossibleStrings.push_back(oStrList);
   oStrList.clear();
   oStrList.push_back("c");
   pVar->lst_PossibleStrings.push_back(oStrList);
   //add the variable to parser
   m_Parser.AddVariable(pVar);

4. Create the template - create template elements and push them sequentially to the template
   C++

   //create template
   CTemplate* pTemplate = new CTemplate;
   //now create elements and append to template
   //we create the template X+a here. Therefore there are two elements
   CTemplateElement* pElement = new CTemplateElement;
   pElement->b_IsVar = true;
   pElement->s_Str = "X";
   pTemplate->lst_Elements.push_back(pElement);
   pElement = new CTemplateElement;
   pElement->b_IsVar = false;
   pElement->s_Str = "a";
   pTemplate->lst_Elements.push_back(pElement);

5. Create the string to parse
   C++

   //we create the string ab+c+a here
   CStrList oStrList;
   oStrList.push_back("ab")
   oStrList.push_back("c")
   oStrList.push_back("a")

6. Call the ParseStrList method of parser
   C++

   CVariableValueSolutionSet* pSolutionSet = 
       m_Parser.ParseStrList(oStrList, pTemplate);

Classes in the tool:
• CStrList - This is derived from std::list<CString>
• CTemplateElement - stands for one element in the template. This can be either a variable or a constant (marked by the flag b_IsVar). If this is a variable the member s_Str will contain the variable name or the string otherwise.
• CTemplate - consists of a list of CTemplateElement
• CVaiable - stands for a variable
• CVariableContainer - this class is used for internal operations. User does not have to bother about this.
• CVariableValueSolution - represents one solution. it consists of a map where key is the variable name and the value is the string assigned to the variable
• CVariableValueSolutionSet - A set of operations which is the output of a parse operation
• CParser - does the parsing.

*After using the CVariableValueSolutionSet object which is returned by CParser::ParseStrList method you must destroy it. Destroy the template also.

pSolutionSet->Destroy();
pTemplate->Destroy();

No need to delete the variables because the parser object will delete them in its destructor.

TokenizeString method : This is a global method used in this tool. Its declaration is as follows.

void TokenizeString(CString sStr, list<CString> lstSeperators, 
    list<CString>& lstSubStr, list<CString>& lstTokens)

• sStr - string to tokenize
• lstSeperators - token list
• lstSubStr - contains the parsed strings in order (output argument)
• lstTokens - contains the parsed tokens in order (output argument)

You may find this method useful in your applications.

Points of Interest

I arrived at this algorithm after several other unsuccessful attempts. A recursive function was used to implement the algorithm. Are there any standard algorithms to do this kind of thing?

I used this algorithm for parsing words and sentences successfully. If someone uses this for analyzing big texts please do let me know about the results, especially the performance.

Can someone extend this to handle empty variables as well?

History