The Generalized Theory of GA

• Download exe - 17.8 KB
• Download source code - 35.9 KB

Introduction

This is a demonstration of how to use GA in more specific constraints. Most GA implementations focus on using chromosome as a disconnected type. The chromosome structure would be like this: A-B-D-F-R-... Or in binary: 101010101 (= integer number). What will we do if we have more than one variable to seek? The obvious answer will be: make your chromosome bigger and for each extra variable, add new genes (cells) in the chromosome.

Example: x1, x2, x3 are three variables that will be contained in the chromosome like this: 101 111 001 (here, the genotype for x1 is 101, the genotype for x2 is 111, and the genotype for x3 is 001).

Okay, now we have a new constraint: the variables are real and each variable has its own real range: Xi from [Ri1, Ri2] where: ? < i.

Now you think of this: divide the chromosome to parts, as is mentioned, and preserve the additional genes in each part to represent the fractional part of that variable and a new gene to represent the variable's signal. But there is no mathematical proof that this will work well for any fitness function [try to maximize (Cos Xi * 0.0000001) + 1, and you can see that the fractional parts here are useless]. Besides, it is a waste of time retrieving the fractional part for each variable and reformatting the variables from the integral and fractional parts and checking the variable's range and taking care of accuracy...

Here are the proved laws for our constraints, these laws simplify everything:

• Xi belongs to [Bi, Ai]
• Calculate D = (Bi - Ai) * 10^p (where p is precision)
• Calculate biggest m: where 2^m - 1 < D
• Calculate Frac = (Bi - Ai) / ( 2^m - 1)

Now, to retrieve the real values from the chromosome, multiply the (integer) numerical value of the chromosome with Frac and then calculate the fitness... Of course, you should calculate Frac for each real variable only at the beginning of the program (before GA starts). You can see that Frac should be a global variable to be seen in the fitness function, or you must pass it to every sub in your code.

Background

A basic knowledge of the language and genetic programming.

Using the code

I assume that the reader already know GA (dozens of free articles on GA can be found in the Internet). I will not explain GA here, but will talk about the general points. The program will show this text:

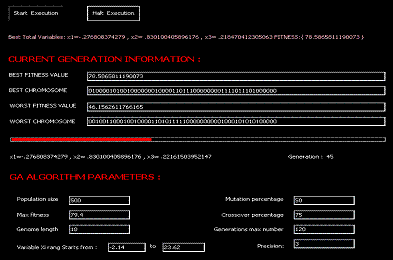
Maximize function: (max fitness)79.45-segma(i=1:3,Xi^2) where ?<= Xi <= ?

Now if you change the (max fitness) value in the textbox near the label 'Max fitness', then the text shown by the program will be changed to your new function, and this will be the new function to maximize. In my program, I made three variables in the same range to simplify my point. You can make ranges different, but you will need to calculate a new FRAC for each variable. Unlike normal GA, I keep the best variables in the entire work of GA during all generations, to inform the user of the best results.

Private Sub Command2_Click(ByVal eventSender As System.Object, _
        ByVal eventArgs As System.EventArgs) Handles Button1.Click 

     ' super_fitness is best variables fitness i got during all generations
     super_fitness = 0
     ''' init best results
     '''you can let this if you want to show permenent best results 

     Label1.Visible = False
     ''''' best variables unhide /user may start
     ''''' the program again after halt or finish
     Dim fir As Object
     ''take lower upper limits of variable's rang
     ai = CType(Text13.Text, Double)
     bi = CType(Text14.Text, Double)
     pre = CType(Text15.Text, Double) ''  precision
     ''calc accurding to laws in introduction
     fir = (bi - ai) * (10 ^ pre)
     mi = 0 

    Do While (2 ^ mi - 1) < fir ''calc accurding to laws in introduction
        mi = mi + 1 
    Loop
    frac = (bi - ai) / (2 ^ mi - 1) ''calc frac
    ' MsgBox(frac) 
    Main_pro()
End Sub 

Public Sub Main_pro()
    Dim a As Short 
    Dim a1 As Double 
    Dim a2 As Short 
    Dim a3 As Double 
    Dim a4 As Double 
    a = Val((Trim(Text7.Text))) 
    a1 = Val(Trim(Text8.Text)) 
    a2 = Val(Trim(Text9.Text))
    a3 = Val(Trim(Text10.Text))
    a4 = Val(Trim(Text11.Text)) 
    a5 = Val(Trim(Text12.Text)) 
    Call BuildPopu(a, a2 * 3, a1, a1, a3, a4) ''init GA
    'because we have 3 variables xi 
    Evolve((frac))
    'Start GA iteration and stop when generations
    'are done or user halted execution
End Sub

Points of Interest

We can use GA to determine the best possible number of layers in a neural network: each chromosome will represent the number of layers. The fitness function will make a NN with the specified number of layers. The function will train it with a number of examples, and will test it after that (random examples), and we will estimate the accuracy of this new NN using the calculation: Ratio (Number of right answers/ Number of questions). The fitness of this chromosome will be assigned this Ratio, other GA stages stay the same.

We can use GA to determine the best possible number of neurons in each layer: by dividing the chromosome to parts, each part represents the number of neurons in one layer. The next part will be used in the same way for the next layer of neurons, and so on.. In a similar fitness function, we will reconstruct the NN for every chromosome, train it, test it, assign fitness..

History

• Last updated: 21-5-2007