N-gram and Fast Pattern Extraction Algorithm

• Download demo project - 24.3 KB
• Download source files - 29.6 KB

Contents

• Introduction
• Background
  • N-gram
  • Pattern Extraction
• Algorithm Idea for Variable Length Pattern Extraction
• Algorithm Pseudo Code
• Code Description
  • ConstructPatterns
  • GetPatterns
  • GetPatternCount
• Points of Interest
  • Algorithm Accuracy
  • Cross-Document Co-reference
  • DIPRE: Dual Iterative Pattern Relation Expansion
• Updates
• References
• Thanks to...

Introduction

In this article, I introduce a very fast algorithm to extract text patterns from large size text and give statistical information about patterns' frequency and length. Actually, the idea of this algorithm came to me when one of my friends asked me to give him an idea for extracting patterns from text. I told him immediately that he could use the LZW compression algorithm, take the final dictionary and drop the compressed buffer, and then he could have a dictionary containing all text patterns with each pattern frequency. I don't know if he understood me or not, but I decided to do it later. If pattern word count is fixed (N), then it is a generation for N-gram of the input sequence.

Background

N-gram

An n-gram is a sub-sequence of n items from a given sequence. n-grams are used in various areas of statistical natural language processing and genetic sequence analysis. The items in question can be characters, words or base pairs according to the application. For example, the sequence of characters "Hatem mostafa helmy" has a 3-gram of ("Hat", "ate", "tem", "em ", "m m", ...), and has a 2-gram of ("Ha", "at", "te", "em", "m ", " m", ...). This n-gram output can be used for a variety of R&D subjects, such as Statistical machine translation and Spell checking.

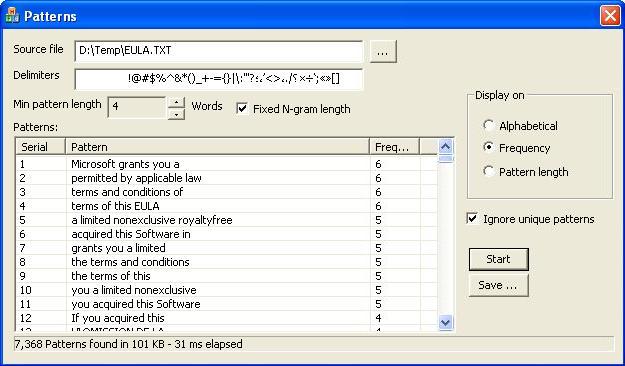
Pattern Extraction

Pattern extraction is the process of parsing a sequence of items to find or extract a certain pattern of items. Pattern length can be fixed, as in the n-gram model, or it can be variable. Variable length patterns can be directives to certain rules, like regular expressions. They can also be random and depend on the context and pattern repetition in the patterns dictionary.

Algorithm Idea for Variable Length Pattern Extraction

The algorithm introduced here is derived from the LZW compression algorithm, which includes a magic idea about generating dictionary items at compression time while parsing the input sequence. If you have no idea about LZW, you can check it out at my article, Fast LZW compression. And of course, the algorithm inherits the speed of my implementation to LZW, plus extra speed for two reasons:

1. The parsing item is a word, not a letter
2. There's no destination buffer, as there is no need for a compressed buffer

The algorithm uses a binary tree to keep extracted patterns that give the algorithm excellent speed at run-time to find and fetch new items to the dictionary. Let us discuss the algorithm pseudo code. We have some figures to clarify the idea with an algorithm flow chart and a simple example.

Example: the input words sequence w0w1w2w3w4w0w1w5w6w7w2w3w4w0w1w5w6

Assume n equals 2; then the initial pattern will be w0w1. After applying the algorithm steps, the resultant dictionary would be as in the fourth column:

Algorithm Pseudo Code

ConstructPatterns(src, delimiters, n, fixed)
{
    des = AllocateBuffer()
    Copy(des, src)
    DiscardDelimiters(des, delimiters)
    dic = InitializePatternsDictionary()

    pattern = InitializeNewPattern(des)
    While(des)
    {
        node = dic.Insert(pattern)
        if(!fixed AND node.IsRepeated)
            AddWordToPattern(des, pattern)
        else
            pattern = InitializeNewPattern(des)
        UpdateBuffer(des)
    }
}

Code Description

ConstructPatterns

This function receives the input buffer, copies it to a destination buffer, and parses it to add found patterns to the dictionary. The constructed dictionary is a binary tree template CBinaryTree<CPattern, CPattern*, int, int> m_alpDic with a key of type CPattern.

void CPatternAlaysis::ConstructPatterns(BYTE *pSrc, int nSrcLen,
    LPCSTR lpcsDelimiters /*= NULL*/,
    int nMinPatternWords /*= 2*/,
    bool bFixedNGram /*= false*/)
{
    // discard initial spaces
    ...
    // allocate destination buffer
    ...
    // discard delimiters
    ...
    // discard repeated spaces
    ...
    // initialize dictionary
    m_alpDic.RemoveAll();
    // tree node to keep last success search to start with
    CBinaryTreeNode<CPattern, int>* pNode = m_alpDic.Root;
    // left m_alpDic Samples points to the source buffer
    int nPrevLength;
    CPattern node(m_pDes, GetPatternLength(
        m_pDes, nPrevLength, nMinPatternWords));
    // scan the input buffer
    while(node.m_pBuffer < m_pDes+nDesLen)
    {
        pNode = m_alpDic.Insert(&node, -1, pNode);
        pNode->Key.m_nFrequency = pNode->Count;
        if(bFixedNGram == false && pNode->Count > 1)
        // (repeated pattern), increment node length
        // by a new word length
        node.m_nLength += AddWordToPattern(node.m_pBuffer+node.m_nLength);
        else
        {   // initialize node to next entity
            node.m_pBuffer += nPrevLength;
            node.m_nLength = GetPatternLength(node.m_pBuffer,
                nPrevLength, nMinPatternWords);
            // initialize binary tree search root
            pNode = m_alpDic.Root;
        }
    }
}

Note: The first good point in this function is that it allocates one buffer for the dictionary and all dictionary nodes point to their start buffer, keeping their buffer length in the class CPattern. So, no allocation or reallocation is done during the algorithm.

class CPattern
{
public:
    CPattern()    {}
    CPattern(BYTE* pBuffer, int nLength)
    {
    m_pBuffer = pBuffer, m_nLength = nLength;
    }
    CPattern(const CPattern& buffer)
    {
    *this = buffer;
    }

public:
    BYTE* m_pBuffer;
    int m_nLength;
    int m_nFrequency;
    inline int compare(const CPattern* buffer);
    {    ...  }
    inline void operator=(const CPattern* buffer)
    {
    m_pBuffer = buffer->m_pBuffer;
    m_nLength = buffer->m_nLength;
    }
};

The function does the steps of the pseudo code. The second good point is the usage of a binary tree CBinaryTree to keep the dictionary, with a very good trick here:

The function Insert() of the tree takes a third parameter to start the search from. In normal cases, this parameter should be the tree Root. However, if a pattern is found and a new word is added to it, then we can start the search for the pattern from the current node, as it must be under current node. This is because it is only the previous pattern plus a new word.

In the case of a new pattern, we should start the search from the tree root, so we have this line at the bottom of the function:

// initialize binary tree search root
pNode = m_alpDic.Root;

GetPatterns

This function doesn't construct patterns. It just retrieves the constructed patterns with three types of sort: Alphabetical, Frequency and Pattern length. The returned patterns are stored in a vector of patterns (OUT vector<CPattern*>& vPatterns).

1. Alphabetical

   C++

   CBinaryTreeNode<CPattern, int>* pAlpNode = m_alpDic.Min(m_alpDic.Root);
   while(pAlpNode)
   {
       if(pAlpNode->Count > 1 || !bIgnoreUniquePatterns)
           // ignore unique pattern
           vPatterns.push_back(&pAlpNode->Key);
       pAlpNode = m_alpDic.Successor(pAlpNode);
   }

2. Frequency

   C++

   // construct a new dictionary to sort stored patterns
   // depending on frequency
   CBinaryTree<CValue<int>, int, vector<CPattern*>,
       vector<CPattern*>* >  displayDic;
   CBinaryTreeNode<CPattern, int>* pAlpNode = m_alpDic.Min(m_alpDic.Root);
   while(pAlpNode != NULL)
   {
       if(pAlpNode->Count >    1 || !bIgnoreUniquePatterns)
           // ignore unique pattern
           displayDic.Insert(pAlpNode->Count/*frequency*/)->
               Data.push_back(&pAlpNode->Key);
       pAlpNode = m_alpDic.Successor(pAlpNode);
   }
   // iterate through the binary tree to get sorted pattern
   // (depend on frequency)
   CBinaryTreeNode<CValue<int>, vector<CPattern*>* pNode =
       displayDic.Max(displayDic.Root);
   while(pNode)
   {
       for(vector<CPattern*>::iterator i = pNode->Data.begin(),
           end = pNode->Data.end(); i != end; i++)
           vPatterns.push_back(*i);
       pNode = displayDic.Predecessor(pNode);
   }

3. Pattern length

   C++

   // construct a new dictionary to sort stored patterns
   // depending on Pattern length
   CBinaryTree<CValue<int>, int, vector<CPattern*>,
       vector<CPattern*>* >  displayDic;
   CBinaryTreeNode<CPattern, int>* pAlpNode = m_alpDic.Min(m_alpDic.Root);
   while(pAlpNode != NULL)
   {
       if(pAlpNode->Count >    1 || !bIgnoreUniquePatterns)
          // ignore unique pattern
          displayDic.Insert(pAlpNode->Key.m_nLength/*length*/)->
              Data.push_back(&pAlpNode->Key);
       pAlpNode = m_alpDic.Successor(pAlpNode);
   }
   // iterate through the binary tree to get sorted pattern
   // (depend on Pattern length)
   CBinaryTreeNode<CValue<int>, vector<CPattern*>* pNode =
       displayDic.Max(displayDic.Root);
   while(pNode)
   {
       for(vector<CPattern*>::iterator i = pNode->Data.begin(),
           end = pNode->Data.end(); i != end; i++)
           vPatterns.push_back(*i);
       pNode = displayDic.Predecessor(pNode);
   }

GetPatternCount

This function retrieves the stored patterns count.

int CPatternAlaysis::GetPatternCount()
{
    return m_alpDic.Count;
}

Points of Interest

1. Algorithm Accuracy

   The algorithm doesn't give accuracy about pattern frequency in the case of variable length patterns (not n-gram with fixed n). That is because the algorithm constructs patterns while parsing the sequence and checks each constructed pattern with the dynamic dictionary. So, if any pattern is first added to the dictionary, a new pattern is constructed starting from the second word of the previous pattern with length n (min pattern length).

2. Cross-Document Co-reference

   Cross-Document Co-reference is the process of finding a relation between documents. In other words, we can say that two documents are related if the two documents contain similar patterns. This subject is studied in many articles, but I found that the best one is "A Methodology for Cross-Document Coreference" by Amit Bagga and Alan W.Biermann. My algorithm may be helpful to generate patterns that can be taken to find a relation between patterns. The good point here is the very good speed of the algorithm, so it can be used for large numbers of documents like the web. However, directed patterns are better than random patterns to find documents' co-reference.

3. DIPRE: Dual Iterative Pattern Relation Expansion

   This is an algorithm introduced by Sergey Brin to collect related information from scattered web sources. I like this idea very much and invite all of you to read his article and search the web for its implementation or even its flowchart. My algorithm can't be used here, as it collects patterns without any guided information about retrieved patterns. However, the FIPRE algorithm is a semi-directed algorithm, as it guides the initial pattern search with regular expressions to identify the required pattern, like "book title" and "author name." Alternatively, if the algorithm collects mails, it will include all regular expressions for mails like that:

   [^ \:\=@;,,$$**++\t\r\n""'<>/\\%??()&]+@[Hh]otmail.com
   [^ \:\=@;,,$$**++\t\r\n""'<>/\\%??()&]+@[Yy]ahoo.com
   [^ \:\=@;,,$$**++\t\r\n""'<>/\\%??()&]+@(AOL|aol|Aol).com

Updates

• 10/09/2007: Posted version v0.9000
• 23/09/2007: Updated the source file vector.cpp to initialize the vector buffer with zeros
• 31/10/2007: Updated the header file vector.h to solve "insert" function bug

References

• N-gram from Wikipedia, the free encyclopedia
• A Methodology for Cross-Document Coreference by Amit Bagga and Alan W.Biermann

Thanks to...

God