Introduction
This article describes a fast algorithm to pack a series of rectangles of varying widths and heights into a single enclosing rectangle, with no overlap and in a way that minimizes the amount of wasted space in the enclosing rectangle. An implementation of the algorithm is in the download, along with a web site that graphically shows step by step how the algorithm arrives at the optimal enclosing rectangle.
Having an algorithm like this is important when generating CSS Sprites, which are used to speed up image loading when loading a web page. With this technique, instead of loading all images on the page one by one, you combine them into a single larger image - called a sprite - and load that in one go. This way, you prevent the overhead of the browser having to request each individual image from the server one by one, which can be significant when loading lots of small images. Using some CSS, you can make the individual images contained within the sprite appear on the page individually. This technique is further described in chapter 12 of my book ASP.NET Site Performance Secrets.
It would definitely be possible to combine the images manually with a graphics program. But then each time you add or remove an image, you have to manually redo the sprite. Much better to have the sprite generated automatically, ideally on the fly when the page loads. However, that means you want a fast algorithm to generate the sprite, even if you cache the result for subsequent page loads.
Additionally, you want the algorithm to pack the images in the sprite in a way that minimizes the overall size of the sprite - the smaller the size, the less time it takes the browser to load the sprite and the less bandwidth you incur:
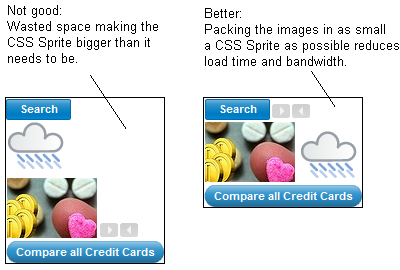
To simplify things a bit, you can think of the images as rectangles, and of the sprite as an enclosing rectangle. It than becomes a matter of finding the enclosing rectangle with the smallest area (width x height) in which you can pack all the rectangles. The rectangle packing algorithm described in this article is designed to do this relatively quickly so it can be used to generate sprites on the fly, and to do a reasonable job of finding the smallest enclosing rectangle. Note that it isn't guaranteed to generate the absolute best enclosing rectangle every time, because that would take a lot longer.
Oh, by the way, if you like this article, please vote for it. That way I know people appreciate my work.
Contents
Installation
The download contains a Visual Studio 2010 solution with:
- A simple ASP.NET web site - run this to see graphically how the algorithm step by step arrives at the best enclosing rectangle. You'll see a form with various parameters - it's easiest to run it with the default values first and then experiment a bit. Full instructions are provided on the form. The test site will run faster if you compile in Release mode rather than Debug mode.
- A class project Mapper that contains the code implementing the rectangle packer described in this article.
Trivial Solutions
There are a few trivial solutions on how to pack rectangles into an enclosing rectangle:
- You could string all rectangles together horizontally, like so:

This is very simple and fast, and would actually be optimal if all rectangles had the same height.
- Or you could string all rectangles together vertically, like so:

This is also very simple and fast, and would actually be optimal if all rectangles had the same width.
However, these solutions leave a lot of wasted space when the rectangles are of varying width and height. They are also a bit boring. So the rest of this article focuses on a solution that does minimize wasted space when the rectangles are of varying width and height, and that is also reasonably fast and simple.
Basic Algorithm
The basic algorithm for packing rectangles into an enclosing rectangle of minimum size is described in, for example, Richard E. Korf's paper: Optimal Rectangle Packing: Initial Results.
- Sort the rectangles by height, greatest height first.
- Start off with an enclosing rectangle that is as high as the highest rectangle, and that has unlimited width.
- Place the rectangles in the enclosing rectangle one by one, starting with the highest rectangle and ending with the lowest rectangle. Put each rectangle as far left as possible. If there are several left most locations, use the highest one. For example:





- Make the width of the enclosing rectangle equal to the total width taken by the rectangles. That is, move the right edge of the enclosing rectangle to left until it touches the right edge of the right most rectangle. That way, the enclosing rectangle is no wider than needed.
- Did you manage to place all rectangles in the enclosing rectangle? In that case:
- If the enclosing rectangle you've got now is the smallest "successful" enclosing rectangle so far, store this enclosing rectangle as the best enclosing rectangle so far.
- It's time to try a smaller enclosing rectangle - decrease the width of the enclosing rectangle by one.
- However, if you did not manage to place all rectangles, the enclosing rectangle was obviously too small. In that case, increase the height of the enclosing rectangle by one.
Note that reducing the width and increasing the height means in effect that we're testing the range of enclosing rectangles from low and wide to high and narrow. For example, after the width has been decreased a few times and the height increased, you may get the following sequence:





- If the total area (width x height) of the enclosing rectangle you have now is smaller than the total area of all the rectangles you're going to try to place inside it, then this is obviously not a viable enclosing rectangle. Increase the height by one until you get a viable enclosing rectangle. Then go to the next step.
- If the enclosing rectangle you've got now is bigger than the best enclosing rectangle so far, there is no point in testing this enclosing rectangle. Decrease the width by one and go back to step 7 to make sure it is now not too small. Otherwise go to the next step.
- If your new enclosing rectangle is narrower than the widest rectangle, you can stop now, and report the best enclosing rectangle you found so far. This is because the algorithm never increases the width of the enclosing rectangle, and if the widest rectangle won't fit, there is obviously no point in testing the enclosing rectangle.
- Now that your new enclosing rectangle is neither too small nor too big, go back to step 3 to see if you can place all rectangles inside it.
This algorithm has been implemented in method Mapping in the class MapperOptimalEfficiency in the Mapper project in the download.
Later on, we'll see how this basic algorithm can be made a lot faster. But first, let's see how to actually place the rectangles in the enclosing rectangle, and above all how to keep track of where there already are rectangles so we don't overlap a new rectangle with an existing rectangle.
Placing Rectangles in a Given Enclosing Rectangle without Overlapping Other Rectangles
Step 3 of the basic algorithm above says "Place the rectangles in the enclosing rectangle one by one, starting with the highest rectangle and ending with the lowest rectangle. Put each rectangle as far left as possible. If there are several left most locations, use the highest one."
In order to find the left most / highest location where a rectangle with given width and height can be placed without overlapping other rectangles, we need to use some data structure to store which areas within the enclosing rectangle are now occupied. And this data structure must make it both simple (that is, less error prone) and fast to find the left most / highest location where the rectangle can be placed.
It would be possible to use a two dimensional array of booleans with one cell for every pixel in the enclosing rectangle. Each boolean would indicate whether the pixel is occupied by a rectangle or free. However, you'd need to visit lots of pixels when finding a place for a rectangle, making this option simple but inefficient.
An alternative would be to store the width/height and X/Y offsets of each rectangle within the enclosing rectangle. This data structure would have far fewer individual items than the two dimensional pixel array, but working out the left most / highest location with enough room for a given rectangle with this data structure turned out to be either very complex or very slow.
The solution I came up with was to use a dynamic two dimensional array of occupied/free booleans, but to store a width with each column and a height with each row, so the number of columns and rows can be kept to a minimum. This minimizes both complexity and the number of cells that need to be visited (and therefore time spent). Here is how this works when adding rectangles (white cells are unoccupied, light green cells are occupied, and dark green cells have just been occupied by the last added rectangle):
- Initially, there is one row with the same height as the enclosing rectangle, and one column with the same width as the enclosing rectangle. Which means there is only one cell.

- When adding the first rectangle, finding the left most / highest cell is easy, because there is only one. Establishing that it is big enough for the rectangle is also easy. So we go ahead and place the rectangle in the upper left corner of the cell.
We now have a cell which is partly occupied and partly unoccupied. However, a cell can be in only one state. To fix that, split the single row and the single column, so we get four cells that are all either occupied or unoccupied:

- Time to add the second rectangle. First check the left most column. Visit all cells in that column from the top most to the bottom most until you find a free cell. Then see whether you can place the rectangle there.
It turns out there is a free cell in the left most column, but there is not enough vertical space there to place the rectangle. So move to the column to the right and go through the same steps as with the left most column.
With this second column, the top most cell is free, and it is big enough for the rectangle, so that's easy. Place the rectangle there. As was the case with the very first rectangle, here too the rectangle is smaller than the cell - leading to a cell that is partly occupied, partly unoccupied. So split the row and column where the cell is located to ensure all cells are either occupied or unoccupied again. Note that as a result, the one cell that was occupied by the first rectangle is now split into two, which is fine.

- The third rectangle goes through the exact same process. However, because this rectangle is a bit lower, there is enough space in the free cell in the left most column for the rectangle. Again, the row and column that intersect at the cell are split, to ensure all cells are either occupied or unoccupied.

- The fourth rectangle goes through the same process. There is not enough vertical space left over in the left most column, so try the one to its right. The highest free cell in that column turns out to be high enough to accommodate the rectangle, but it is not wide enough. So test the columns towards the right to see if there are enough free cells there to accommodate the rectangle. It turns out that the original column and the one to its right together have enough horizontal space for the rectangle, so the rectangle can be placed using the two cells. Again, a row and a column are split to make sure all cells are either occupied or unoccupied.

- For the fifth rectangle, again the columns are checked from left to right. The second column has one free cell, but there is not enough vertical space for the rectangle. The third column has two isolated free cells, but neither is high enough in its own right, and neither can be combined vertically with another cell to find enough vertical space for the rectangle.
In the fourth column, there is a free cell that in itself is neither high nor wide enough for the rectangle. So check the cells to the right of the column and the cells in the row below to see if enough free cells can be combined to accommodate the rectangle. In this case, that turns out to be possible. Again, a row and column split occurs to make sure all cells are either occupied or unoccupied.

You can see lots more examples (and rectangles) by running the web site contained in the download. This also shows situations where not every rectangle can be placed.
The code that finds the left most / highest cell where a rectangle can be placed and that checks neighboring cells, etc. is in the Canvas class in the Mapper project in the download. The two dimensional dynamic array is implemented in the DynamicTwoDimensionalArray class. Because it is heavily used, that class is highly optimized for performance, especially when splitting rows and columns.
Improvements over the Basic Algorithm
While studying the test cases generated by the test site in the download, the following improvements became clear. Those improvements were worked into the code in the download. I didn't find these in the literature, so you read about them here first:
When Reducing Enclosing Rectangle Width, Increase Height Sufficiently
Have a look at the following enclosing rectangle that was produced during an iteration of the basic algorithm:

According to the basic algorithm, you should reduce the width of the enclosing rectangle by 1 and then try again to place all rectangles. However, if you simply reduce the width by 1, you know that the dark green rectangle that sits against the right hand border of the enclosing rectangle cannot be placed anywhere, so the next try will fail for sure.
Additionally, the algorithm says to increase the height of the enclosing rectangle by 1 when that failure happens. However, because the dark green rectangle is 10 pixels high, you know that increasing by 1 will not be enough. So following the basic algorithm will definitely create 10 failed attempts to place all rectangles, which is expensive and unnecessary.
The optimization is to record the height of the tallest rectangle that sits against the right hand edge of the enclosing rectangle. If you're successful in placing all rectangles and you reduce the rectangle's width by 1, then also increase the height of the enclosing rectangle by the height of the tallest right flushed rectangle. That gives the algorithm a chance to find a new spot for the tallest right flushed rectangle within the new enclosing rectangle:

After Failure to Place All Rectangles, Increase Height Sufficiently
Have a look at the sequence below. Here the algorithm places 4 rectangles, but then fails to place the fifth rectangle.
| 1 | 2 | 3 | 4 | Failed to
place rectangle |

| 
| 
| 
| 
|
After this failure, the basic algorithm would increase the height of the enclosing rectangle by 1 and try again to place the rectangles. However, with an increase of only 1, the first 4 rectangles are likely to be placed in the exact same locations, leading again to a failure to place the fifth rectangle. The algorithm would then increase the height by 1 again and try again, possibly creating the same situation, etc. All this fruitless trying takes a lot of time.
Instead of increasing the height by 1, it needs to be increased by the smaller of:
- The height of the rectangle that could not be placed; and
- The height by which the enclosing rectangle needs to be increased to ensure that the first 4 rectangles will be arranged differently - which would give the algorithm at least a chance to place the fifth rectangle.
By picking the minimum of the two, you're more likely to wind up with the smallest possible enclosing rectangle.
Figuring out the height mentioned in point 2 above is not all that hard when you realize that the algorithm tries to place each rectangle in the left most column first, and if that fails, moves to the column to the right and tries again, etc. Each time it fails to place the rectangle in a column, that is because the free space in the bottom of that column is lower than the rectangle itself - there is a free height deficit.
For example, for the second rectangle, the free height deficit in the first column is 30px:

That is, if the enclosing rectangle had been 30px higher, the second rectangle could have been placed in the left most column.
Likewise, the free height deficit for the third rectangle in the left most column is 25px, and in the second column it is 15px. So if the enclosing rectangle had been 15px higher, the third rectangle could have been placed differently:

The free height deficit for the fourth rectangle in the left most column is 10px. So if the enclosing rectangle had been 10px higher, the fourth rectangle might have been placed in the first column:

We want to increase the height of the enclosing rectangle by the minimum required to ensure that the rectangles can be arranged differently. Here, the smallest free height deficit for all rectangles for all columns is 10px (applies to the fourth rectangle in the left most column). Seeing that the fifth rectangle that failed to be placed is higher than 10px, we need to increase the height of the enclosing rectangle by 10px to have any hope of placing the fifth rectangle at the next try:
This means that in order to prevent a lot of failed enclosing rectangles, the algorithm simply needs to keep track of the smallest free height deficit when it tries to place a rectangle in a column. Then when it fails to place a rectangle, it needs to increase the height of the enclosing rectangle by that smallest free height deficit - or by the height of the rectangle that couldn't be placed if that is smaller.
This optimization is not guaranteed to lead to a successful enclosing rectangle at the next try. For example, at the new height, the enclosing rectangle may be bigger than the best enclosing rectangle so far, in which case the algorithm will start to reduce its width. Because of this, it may fail to place all rectangles at the next try because of the reduced width. What this optimization does do is prevent a lot of tries that have no hope of succeeding.
Trade off Enclosing Rectangle Size Against Speed
If you decide you can live with a given level of wasted space, one way to reduce the time taken to generate the enclosing rectangle is to tell the code to stop trying to get a smaller enclosing rectangle once it has reached that level.
Another way to improve speed is to tell the algorithm to stop after it has found a certain number of successful enclosing rectangles that can contain all rectangles. You would probably set the limit at one or two. That would be attractive if you found that this way you generally get results that are good enough while getting an almost guaranteed speed boost.
To allow you to make these choices, a second constructor has been provided for the MapperOptimalEfficiency class, with additional parameters to set these two cut offs.
Software Interface to the Rectangle Packer
The rectangle packer described in this article has been implemented in the Mapper project in the download. It exposes a well defined interface to the outside world. The test site uses that interface. Below is a description of the interface, to make it easier to study the code or to use the code in your own projects.
You'll find that the code refers to images and sprites rather than rectangles and enclosing rectangles. This is because it was written as part of an (as yet unfinished) project to build an automated on-the-fly sprite generator.
Interfaces
To make the code easily extensible, the software interface is defined using C# Interfaces. That way, you can provide your own implementation for one class while reusing the other classes.
- The rectangle packer is defined using the
IMapper C# interface. It exposes a single method Mapping. That method takes a collection of objects implementing IImageInfo, and returns an object implementing ISprite. In other words, you give it the collection of images you want to combine into a sprite, and it produces the sprite for you. IImageInfo simply exposes the width and height of the image - which is all that the rectangle packer needs. Note that by itself it doesn't represent a real image with an image URL, etc. It is called IImageInfo rather than IImage, because the System.Drawing namespace already contains an Image class. - The
ISprite object returned by the method Mapping simply exposes the width, height, and area of the sprite, and the collection of images contained within the sprite. Similar to IImageInfo, it doesn't by itself define an image, because the code implements a rectangle packer that works with rectangles, not with physical images. Because we need to store at what X and Y offset within the sprite each IImageInfo is located, this collection uses IMappedImageInfo, which exposes the IImageInfo and its X and Y offset.
As a result, the following C# interfaces describe the complete software interface of the rectangle packer:
public interface IMapper<S> where S : class, ISprite, new()
{
S Mapping(IEnumerable<IImageInfo> images);
}
public interface IImageInfo
{
int Width { get; }
int Height { get; }
}
public interface ISprite
{
int Width { get; }
int Height { get; }
int Area { get; }
List<IMappedImageInfo> MappedImages { get; }
void AddMappedImage(IMappedImageInfo mappedImage);
}
public interface IMappedImageInfo
{
int X { get; }
int Y { get; }
IImageInfo ImageInfo { get; }
}
What this means is that if you want to follow in my footsteps and build your own rectangle packer that works with the test site in the download, all you need to do is implement the C# interface IMapper. If you want to compare the performance of your implementation against mine using the test site, add your implementation to the mappers array defined in method Generate in the file default.aspx.cs.
On the other hand, if you want to use the rectangle packer I've done but use your own image class and/or sprite class, simply make sure they implement IImageInfo or ISprite. If you wanted to write a CSS Sprite generator, you'd probably write image and sprite classes that represent real images while still implementing IImageInfo and ISprite.
Implementation
The C# interfaces have been implemented in the Mapper project in the download with these classes:
| Interface | Implementation |
|---|
IMapper | There are three implementations:
MapperOptimalEfficiency - The rectangle packer described in this article. Good for packing rectangles (that is, IImageInfo objects) of varying widths and heights.
The constructor of MapperOptimalEfficiency takes a parameter of type ICanvas. That interface has been implemented in the class Canvas, so you could simply instantiate a Canvas object and pass that to the MapperOptimalEfficiency constructor, as shown below. The Canvas object is used to figure out whether a given set of rectangles will fit within an enclosing rectangle of a given fixed size. If you have found a better way to do that, you could build your own class implementing ICanvas and pass that to the MapperOptimalEfficiency constructor.
MapperHorizontalOnly - Simply strings all IImageInfo objects together horizontally. Optimal if they all have the same height. MapperVerticalOnly - Simply strings all IImageInfo objects together vertically. Optimal if they all have the same width.
|
IImageInfo | ImageInfo. This lives in the App_Code folder in the test site rather than the Mapper project, because it is very application specific. For example, in the actual CSS Sprite generator I'm working on, this class will contain the image file name, etc., but the version in the download only stores width and height. |
IMappedImageInfo | MappedImageInfo |
ISprite | Sprite. Similar to ImageInfo, this lives in the App_Code folder in the test site rather than the Mapper project, because it too is very application specific. |
Usage
To use the rectangle packer software in your own project:
- Create a class implementing
IImageInfo, or use the ImageInfo class I did. - Create a class implementing
ISprite, or use the Sprite class I did. - Instantiate a class implementing
IMapper, such as MapperOptimalEfficiency:
using Mapper;
Canvas _canvas = new Canvas();
MapperOptimalEfficiency<Sprite> mapper =
new MapperOptimalEfficiency<Sprite>(_canvas);
- Create an
IEnumerable<IImageInfo> with the IImageInfo objects to be placed in the enclosing rectangle. You could call this rectangles. - Finally, call the
Mapping method:
Sprite sprite = mapper.Mapping(rectangles);
History
- 14th June, 2011: Initial post
