Collaborative Filters - How to build a recommendation system

• Download source - 4.79 KB

Introduction

Ever browsed Amazon and noticed the "Customers That Bought This Item Also Bought These Items" list, or after you've selected a movie on Netflix, recommendations for similar flicks? The ability to find trends in the browsing habits and choices of users has become a must for many customer facing websites. Collaborative Filters are the magic that makes these features possible. In this article, we'll explore one popular implementation of a recommendation system, how it works, and how to incorporate it into your project.

Background

The algorithm we're going to be using to find the trends in our data is called the Pearson Correlation Score. The reason for this choice is simple - it effectively can handle and balance un-normalized data. For example, movie reviews tend to be more neutral when done by a typical user than a critic. The code samples will be written in .NET 3.5 SP1, and we will be using LINQ to traverse parts of the data set. These examples will be written as a console application in order to keep the code snippets simple and to make the overall concepts easier to grasp.

Using the code

First things first, we'll need data structures to hold the recommendations of each product:

public class Recommendation     
{
    public string Name { get; set; }
    public double Rating { get; set; }
}

For simplicity, we'll keep our products in a dictionary with the product name as the key and a List<Recommendation> as the value.

Dictionary<string, List<Recommendation>> productRecommendations = 
           new Dictionary<string, List<Recommendation>>();

In a real system, data would exist in a database, but for this example, we'll hard code our data into the dictionary:

List<Recommendation> list = new List<Recommendation>();
list.Add(new Recommendation() { Name = "Wile E Coyote", Rating = 4.5 });
list.Add(new Recommendation() { Name = "Bugs Bunny", Rating = 2.5 });
list.Add(new Recommendation() { Name = "Elmer Fudd", Rating = 5.0 });
list.Add(new Recommendation() { Name = "Foghorn Leghorn", Rating = 2.0 });
productRecommendations.Add("ACME Industrial Rocket Pack", list);

list = new List<Recommendation>();
list.Add(new Recommendation() { Name = "Wile E Coyote", Rating = 5.0 });
list.Add(new Recommendation() { Name = "Bugs Bunny", Rating = 3.5 });
list.Add(new Recommendation() { Name = "Elmer Fudd", Rating = 1.0 });
list.Add(new Recommendation() { Name = "Foghorn Leghorn", Rating = 3.5 });
list.Add(new Recommendation() { Name = "Daffy Duck", Rating = 1.0 });
productRecommendations.Add("ACME Super Sling Shot", list);

list = new List<Recommendation>();
list.Add(new Recommendation() { Name = "Wile E Coyote", Rating = 1.0 });
list.Add(new Recommendation() { Name = "Bugs Bunny", Rating = 3.5 });
list.Add(new Recommendation() { Name = "Elmer Fudd", Rating = 5.0 });
list.Add(new Recommendation() { Name = "Foghorn Leghorn", Rating = 4.0 });
list.Add(new Recommendation() { Name = "Daffy Duck", Rating = 4.0 });
productRecommendations.Add("ACME X-Large Catapult", list);

list = new List<Recommendation>();
list.Add(new Recommendation() { Name = "Bugs Bunny", Rating = 3.5 });
list.Add(new Recommendation() { Name = "Elmer Fudd", Rating = 4.0 });
list.Add(new Recommendation() { Name = "Foghorn Leghorn", Rating = 5.0 });
list.Add(new Recommendation() { Name = "Daffy Duck", Rating = 2.5 });
productRecommendations.Add("ACME Super Glue", list);

list = new List<Recommendation>();
list.Add(new Recommendation() { Name = "Wile E Coyote", Rating = 4.5 });
list.Add(new Recommendation() { Name = "Bugs Bunny", Rating = 5.0 });
list.Add(new Recommendation() { Name = "Foghorn Leghorn", Rating = 3.0 });
productRecommendations.Add("ACME Jet Powered Roller Skates", list);

Here, we have a collection of products, and each product has a collection of reviews. Each review has a value from 1 to 5 describing how well they liked the product. This value can be based on what you are trying to profile. For example, you could use a value of 1 to represent a user that bought a particular product (with a 0 showing users who did not purchase a product). As long as we have a way to convert the data to a numerical value, the data can be analyzed.

The ability to recommend products is accomplished by being able to find similarities between them. To do that, we use the Pearson Correlation Score. The Correlation Score is a measure of how well two sets of data fit on a straight line. One interesting aspect of the Pearson Score is that it corrects for grade inflation. That is, if one product has consistently higher scores than another, there can still be a perfect correlation — if the difference between the ratings is consistent.

The code for this algorithm:

1. first finds the reviewers that reviewed both products. It then
2. computes the sums and the squared sums of the ratings for the two products, and
3. computes the sum of the reviews of the products. Finally,
4. it uses these results to compute the Pearson Correlation Score, shown in the code below:

List<Recommendation> shared_items = new List<Recommendation>();

// collect a list of products have have reviews in common
foreach (var item in productRecommendations[product1])
{
    if (productRecommendations[product2].Where(x => x.Name == item.Name).Count() != 0)
    {
        shared_items.Add(item);
    }
}

if (shared_items.Count == 0)
{
    // they have nothing in common exit with a zero
    return 0;
}

// sum up all the preferences
double product1_review_sum = 0.00f;
foreach (Recommendation item in shared_items)
{
    product1_review_sum += productRecommendations[product1].Where(
             x => x.Name == item.Name).FirstOrDefault().Rating;
}

double product2_review_sum = 0.00f;
foreach (Recommendation item in shared_items)
{
    product2_review_sum += productRecommendations[product2].Where(
             x => x.Name == item.Name).FirstOrDefault().Rating;
}

// sum up the squares
double product1_rating = 0f;
double product2_rating = 0f;
foreach (Recommendation item in shared_items)
{
    product1_rating += Math.Pow(productRecommendations[product1].Where(
             x => x.Name == item.Name).FirstOrDefault().Rating, 2);

    product2_rating += Math.Pow(productRecommendations[product2].Where(
             x => x.Name == item.Name).FirstOrDefault().Rating, 2);
}

//sum up the products
double critics_sum = 0f;
foreach (Recommendation item in shared_items)
{
    critics_sum += productRecommendations[product1].Where(
            x => x.Name == item.Name).FirstOrDefault().Rating *
    productRecommendations[product2].Where(
           x => x.Name == item.Name).FirstOrDefault().Rating;
}

//calculate pearson score
double num = critics_sum - (product1_review_sum * 
  product2_review_sum / shared_items.Count);

double density = (double)Math.Sqrt((product1_rating - 
  Math.Pow(product1_review_sum, 2) / shared_items.Count) * 
  ((product2_rating - Math.Pow(product2_review_sum, 2) / shared_items.Count)));

if (density == 0)
    return 0;

return num / density;

This algorithm will return a value between -1 and 1, where 1 means the two products have exactly the same ratings. One thing to note is that this algorithm only compares two products, so to calculate scores for our entire catalog, we have to loop through each product, calculating the score:

// grab of list of products that *excludes* the item we're searching for
var sortedList = productRecommendations.Where(x => x.Key != name);

sortedList.OrderByDescending(x => x.Key);

List<Recommendation> recommendations = new List<Recommendation>();

// go through the list and calculate the Pearson score for each product
foreach (var entry in sortedList)
{
    recommendations.Add(new Recommendation() { Name = entry.Key, 
                        Rating = CalculatePearsonCorrelation(name, entry.Key) });
}

return recommendations;

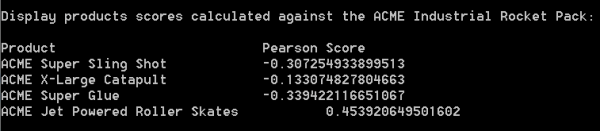
As we can see from the given scores, users who were looking at the Industrial Rocket Pack would also be interested in a pair of Jet Powered Roller Skates.

History

• v1.0: Initial release.