Contents
A heterogeneous container is a container that can store elements of different types. For strongly typed languages like C++, such kind of container isn't a natural or built-in feature. Many solutions exist though, to simulate this heterogeneous property, but they often involve memory space or runtime speed trade-offs.
This article presents a fixed-size heterogeneous container, named tek::record, that tries to achieve the best possible performances in terms of both size and speed. The goal of the article isn't only to list the tek::record functionalities, but rather to explain how such a solution is implemented, going from basic template metaprogramming concepts to advanced optimization techniques.
This chapter lists the most known and popular solutions to implement a heterogeneous container, and their main drawbacks.
In the classical polymorphism solution, the container holds pointers to a base class from which several classes are derived. The heterogeneous property is then achieved through the dynamic type of each element of the collection.
Limitations:
- Virtual functions can't be inlined in this case
- Impossibility to directly use built-in types
- Loss of type identity and traits specific to the derived classes
A container of unions simulates a heterogeneous behavior, since the value of a union can be interpreted through multiple types. However, mere unions have severe limitations:
- They only accept a restricted set of types
- They aren't type-safe
- They must reserve a space at least equivalent to the size of the largest type of the union, resulting in a waste of memory space in a heterogeneous container
Union-like implementations, such as discriminated unions, made their appearance to overcome some of those limitations. One example of such implementation is boost::variant. Those union-like implementations also come with some limitations:
- Waste of space still present
- Slight runtime overhead, depending on the specific implementation.
A tuple is a finite collection of elements. In C++, the implementation of a tuple is a fixed-size container that can hold elements of any type. In such an implementation, element access is resolved statically resulting in no runtime overhead.
Limitations:
- Fixed size
- No dynamic access to elements
We reviewed some popular implementations of a heterogeneous container. This list isn't exhaustive, there are other solutions ( boost::any, void*, ...) that share some of the limitations described above. While examining the drawbacks of each solution, we can notice some sort of gap between the tuple and the other solutions:
- A tuple is the best in terms of both speed and memory but has very few functionalities and provides no dynamic access. Hence, it has a limited use such as simulating multiple return values.
- Other solutions are slower but allow standard and dynamic container operations.
The tek::record container tries to partially fill the gap by providing good performances and a dynamic access to its elements.
Before explaining the implementation of the heterogeneous container, the concept of typelist must be briefly reviewed. If you already know what typelists are, you may jump directly to the next section.
A typelist is a type containing a certain number of types. Its implementation is based on the following template structure:
template < typename T, typename U >
struct typelist {
typedef T element_type;
typedef U next_type;
};
To define a variable number of different types, the typelist structure is declared recursively as follows:
typedef
typelist< int,
typelist < char,
typelist < MyClass,
end_of_list > > > MyTypelist;
The above declaration defines a list of three types: int, char, MyClass. The list is terminated by a special structure, end_of_list, that acts as an end marker. At first sight, a simple access to a type is done as follows:
MyTypelist::element_type MyTypelist::next_type::element_type MyTypelist::next_type::next_type::element_type
However, to be useful and convenient, accessing a type must be done in a generic way, using an index. The implementation of such access is done recursively: going through the next_type type the number of times given by the index.
template < class T, int INDEX >
struct get_type {
typedef typename get_type < typename T::next_type,
INDEX-1 >::type type;
};
template < class T >
struct get_type < T, 0 > {
typedef typename T::element_type type;
};
With the recursive get_type structure, we can now access a type using a static index:
get_type < MyTypelist, 0 >::type;
get_type < MyTypelist, 2 >::type;
We now know enough about typelists to continue. Note that we left out a number of their capabilities. For further details, check out [Alexandrescu] in the References.
As we saw in the Existing Solutions chapter, tuples have some performance advantages over the other heterogeneous containers. They don't waste memory space 1, and accessing an element is very fast. To achieve such performances, the classical implementation of a tuple relies on a template structure that follows the typelist philosophy.
Example:
template < typename T, typename U >
struct tuple {
T element;
U next;
typedef T element_type;
typedef U next_type;
};
An arbitrary number of types can be specified to the structure:
tuple< int,
tuple < std::string,
tuple < MyClass,
end_of_list > > > >
Such declaration will be roughly translated to the following (without including the typedefs):
struct tuple<...> {
int element; struct tuple<...> {
std::string element; struct tuple<...> {
MyClass element; end_of_list next;
} next;
} next;
};
A tuple defines two kinds of indexed access, both of which are performed statically:
- Indexed access to an element type
- Indexed access to an element value
Indexed access to an element type in the list is identical to the get_type structure used in the typelist implementation we saw earlier. Indexed access to an element value is done using a recursive function:
template< int INDEX, typename return_type >
struct get_element {
template< class T >
static return_type Do( T& tup )
{
return get_element< INDEX-1, return_type >::Do( tup.next );
}
};
template< typename return_type >
struct get_element< 0, return_type > {
template< class T >
static return_type Do( T& tup )
{
return tup.element;
}
};
Modern compilers are able to inline the recursive function, as if the value was directly accessed. The return_type template parameter is computed by using the get_type structure. Actually, computing the return type is more complex, since we may add or remove reference and constant qualifiers. For example, if the tek::record is declared as constant, we should return a constant.
The implementation of a tuple is a good base for a high performance, fixed size heterogeneous container. However, a tuple doesn't provide dynamic access to its elements. That's quite logical: what code an expression like myTuple[x], where x is an index given at runtime, the compiler should generate since the type must be determined at runtime along with x ? It's quite probable that the code will be different if it's an int, a std::string, or an user defined class. Since a simple expression like myTuple[x] can't be evaluated by the compiler, the dynamic access will be done using a function, named apply, which takes two parameters:
- A functor, provided by the user, which will be applied to the indexed element
- An index
The functor acts as a visitor 2 and should have an overloaded function for each element type.
Example:
myTuple.apply( Print(),index );
Functor definition:
struct Print {
void operator()( int element )
{
std::cout << "int : " << element << endl;
}
void operator()( double element )
{
std::cout << "double : " << element << endl;
}
void operator()( char element )
{
std::cout << "char : " << element << endl;
}
};
The element parameter will be fed by the apply function. Of course, template functions can be used to factorize the source code if the latter is the same for some or all types.
The implementation of such dynamic access must generate every possible code for each type and select the right one according to the runtime value of the index. The selection can be simply done using an if then else chain or a switch case statement.
Example using switch (pseudo-code):
template < class T >
void apply ( int index, T functor )
{
switch ( index ) {
case 0 : functor ( tuple[0] ); break; case 1 : functor ( tuple[1] ); break; ...
}
}
Note: tuple[x] is pseudo-code. In reality, we have to use the get_element structure.
This implementation is no more than a kind of type switching and, in the OO world, type switching is considered evil because it introduces coupling: each time you add a new type, you must modify the switch accordingly. However, this drawback isn't one for our implementation since we can automatically adapt the type switching to the types specified to our container. This is indeed done easily if we implement the type switching with cascading if then else. A "recursive" template structure will go through the typelist and add an if condition for each type with the right code. In the end, the compiler generates something like this:
if (index == 0)
else
if (index == 1)
else
if (index == 2)
...
Finding the right index this way induces a complexity of O(n). A search algorithm could be generated instead to reduce the complexity but the performance still depends on the number of types handled by the heterogeneous container. The alternative solution is the use of the switch case statement. While the behavior of such statement is the same as the if then else one for the use we make, its implementation, generated by the compiler, may differ greatly depending on the case values.
For example, suppose we want to test a range of values from 0 to 3. We can test all the values within a switch:
switch (x) {
case 0 : ...
case 1 : ...
case 2 : ...
case 3 : ...
}
The above switch statement can be optimized by a decent C++ compiler with the construction of a jump table. Such table contains the instruction address of each case statement. The x value is then used as an index to the jump table. Consequently, the code generated by the compiler is just a jump whose operand is the value pointed by an index in the jump table, which gives roughly the following code instruction:
JUMP ADDR_TABLE[ x ];
The performance of a jump table is constant in terms of complexity, and is better than the performance of the if then else approach most of the time 3. To make the construction of a jump table possible, the case values must be contiguous 4. Testing every possible index of our heterogeneous container fulfills this condition. Hence, the switch case approach is used in our container to implement dynamic access. However, adapting the number of cases to the typelist given to the record is more difficult (see section Pseudo-variadic Behavior Implications).
Since we are in the context of a fixed-size container, out-of-boundary checking can be sometimes superfluous and should be left to the user (see the is_valid_index function in chapter usage). However, the compiler always makes bounds checking to check whether the index is valid for the jump table. Visual C++ proposes the compiler-specific keyword __assume so the programmer can specify that the index is guaranteed to be one of the case values. The compiler can then decide not to make bounds checking.
switch (x) {
case 0 : ...
case 1 : ...
case 2 : ...
default : __assume(0); }
I don't know about other compilers supporting these kind of keywords. At the time of writing, GCC doesn't support such compile-time assumptions. So __assume(0) is just used for Visual C++, other compilers will probably check bounds. As you see, the title of this subsection is "Bounds Checking Elimination", which refers to a compiler optimization, for some languages like Java, that eliminates bounds checking when accessing an element in an array, without modifying in any way the program's integrity and behavior. 5 Consequently, the apply function should then be used when the index is without any doubt valid. If the index validity can't be certified, the is_valid_index function shall be called before the apply function.
Variadic templates isn't supported in the current version of the C++ language, though it is a desirable feature in our case. Users should be able to write with no hassle:
record < int, char > a; record < int, char, double, std::string > b;
instead of using the recursive way:
record < int, < record char < record double , etc.
To simulate variadic templates, default template parameters are used. The default template argument is null_type, a "dummy type" that contains no data and also acts as an end marker for the typelist.
template < class T0 = null_type,
class T1 = null_type,
class T2 = null_type,
class T3 = null_type >
struct record {};
The user can then specify any number of parameters upto a certain limit, 4 in the example. This limit is ultimately parameterizable with a macro (see chapter Usage). Internally, all those template parameters are converted to a tuple:
tuple< T0, tuple < T1, tuple < T2, T3 > > >
Using such kind of limit leads to a compilation problem concerning the switch statement in our apply function. Unlike cascading if then else, we can't use a recursive template structure to generate the right number of case statements. Because of this, we have to implement the apply function so that the number of cases will always be equal to the maximal number of types one record can handle. Suppose we set this limit to 4, our apply function will be something like this:
template < class T >
void apply ( int index, T functor )
{
switch ( index ) {
case 0 : functor ( tuple[0] ); break;
case 1 : functor ( tuple[1] ); break;
case 2 : functor ( tuple[2] ); break;
case 3 : functor ( tuple[3] );
}
}
If the user declares a record< int , char >, the last 2 cases will cause compilation errors. Here are two ways of dealing with this problem.
We could use a structure that encapsulates each case and generates either functor( tuple[x] ) if x is inferior to the number of types the record handles, and nothing otherwise.
Example:
case 0 : SilentCase< 0 > ( tuple, functor ); case 3 : SilentCase< 3 > ( tuple, functor );
But there are still two performance problems:
- The
jump table, generated by the compiler, always contains 4 members (in our example) whereas it could contain less depending on the number of types specified to the record. This is a minor but yet existent waste of space. - Because the number of
cases could be lower, the compiler may miss some optimizations, since when there are very few cases, a better optimization can be used instead of a jump table. The whole apply function might also be easier to inline.
To overcome the last two problems, we must adapt the number of cases in the switch statement to the number of types handled by the record. But, as said earlier, we can't use a recursive structure that adds the right number of case statements, as with an if then else chain. The trick is to generate every possible apply function, each one with a different number of cases. To select the correct function at compile-time, we wrap all those functions in a structure. The latter accepts an int template parameter that will be used to indicate the right number of cases.
Example (pseudo-code):
template < int I >
struct apply_select;
template <>
struct apply_select < 2 >
{
static void apply ( int index, T functor )
{
switch ( index ) {
case 0 : functor ( tuple[0] ); break;
case 1 : functor ( tuple[1] ); break;
}
};
template <>
struct apply_select < 3 >
{
static void apply ( int index, T functor )
{
switch ( index ) {
case 0 : functor ( tuple[0] ); break;
case 1 : functor ( tuple[1] ); break;
case 2 : functor ( tuple[2] ); break;
}
};
...
In the record implementation, the right apply function is called this way:
apply_select< record_size >::apply( index, functor );
This way, only the apply function with the right number of cases will be instantiated and generated by the compiler.
We saw earlier that a functor is used as an argument to the apply function. This functor can define a specific operator() for each type handled by the record, but sometimes, you want a generic process and use a template operator(). For example, suppose that each type of the heterogeneous container has a data member called data. A generic process can be defined by the following functor:
struct MyFunctor {
template < class T >
void operator()( T& element )
{
process( element.data );
}
};
Generic processes are interesting because they may allow the compiler to do an additional optimization concerning the jump table in the apply function. This optimization consists in eliminating branches by merging cases.
For example, consider the following code:
switch (x) {
case 0 : foo(); break;
case 1 : foo(); break;
case 2 : bar(); break;
case 3 : bar(); break;
case 4 : bar(); break;
}
We saw that such code will lead the compiler to generate a jump table:
Pseudo generated code:
jump JUMP_TABLE[x]
label_case_0 : call foo ...
label_case_1 : call foo ...
label_case_2 : call bar ...
label_case_3 : call bar ...
label_case_4 : call bar ...
JUMP_TABLE contents:
| index | label address |
0 | &label_case_0 |
1 | &label_case_1 |
2 | &label_case_2 |
3 | &label_case_3 |
4 | &label_case_4 |
A compiler applying branch elimination will generate the following instead:
Pseudo generated code:
jump JUMP_TABLE[x]
label_case_foo : call foo ... label_case_bar : call bar ...
JUMP_TABLE contents:
| index | label address |
0 | &label_case_foo |
1 | &label_case_foo |
2 | &label_case_bar |
3 | &label_case_bar |
4 | &label_case_bar |
This has numerous advantages because:
- It reduces the code size and favors inlining of the
apply function. - It reduces the number of branch targets which might lead to a performance increase.
- Since it reduces the number of branches, it might allow the compiler to use a better optimization than a
jump table.
The template operator() of MyFunctor seems to apply the same code for each element of a record. However, the code generated by the compiler needs to include the address of each element, therefore it may effectively differ.
To understand the issue, let's look at how the apply function works. The latter internally calls another function that takes as an additional parameter the record data. Here is the declaration of this internal function:
template < class T, class U >
apply_internal( T& record_data, int index, U& functor)
{
switch( index ) {
...
}
}
record_data actually contains all of the elements and has basically the same structure as a tuple. Since we pass the address of a tuple to the apply_internal function, the generated code will reference, for each case, the corresponding element by applying a different offset from the record_data argument:
template < class T, class U >
apply_internal( T& record_data, int index, U& functor)
{
switch( index ) {
case 0 : &record_data case 1 : &record_data + 12 case 2 : &record_data + 26 ...
}
}
But if we pass directly the address of the concerned element instead of the whole tuple, the compiler will have to handle the same reference for each case:
template < class T, class U >
apply_internal( T& element, int index, U& functor)
{
switch( index ) {
case 0 : &element
case 1 : &element
case 2 : &element
}
}
To know the address of the element pointed by the index before going to the apply_internal function, we have to store each element address in a void* array, at the construction of the record. Then the apply function loads the address of the element and uses it as a parameter of the apply_internal function:
template < class U >
void apply (int index, U& functor )
{
apply_internal< record_type >( addrTable[index], x, functor )
}
with apply_internal being defined as follows:
template < class record_type, class U >
void apply_internal( void* element, int index, U& functor)
{
switch( index ) {
case 0 : functor ( * (typename get_type< record_type, 0 >::Type *>) element );
break;
case 1 : functor ( * (typename get_type< record_type, 1 >::Type *>)
element );
break;
}
}
However, this method has several drawbacks:
- It induces overheads: constructing the address table at the beginning and looking up for the element's address for each access
- It is triggered in only few contexts, where the code is the same for some or all elements
- It can be impossible to know whether the code is the same for some or all types if they aren't known while writing the code. Even if they are known, some misleading cases can occur. For example, at the beginning of the chapter, we defined the functor
MyFunctor that does a generic processing on a data member of the element: process(element.data). Even if element.data has the same type for all elements, the data member may have a different offset for each element type, which prevents case merging.
That's why this optimization is disabled by default. It can be enabled by defining the TEK_RECORD_MERGE_APPLY macro (see chapter Usage), but it should be reserved for experimental or profiling purposes.
This section lists the tek::record functionalities. First, here is a simple example to show the basic usage of a tek::record:
#include "tek/record.h"
#include <iostream>
using namespace std;
struct Inc {
template < class T >
void operator()( T& element ) const
{
element++;
}
};
int main()
{
tek::record< int, char, double > myRecord( 2, 'r', 5.25 );
cout << myRecord; cout << myRecord.get<1>(); myRecord.get<0>() = 10; myRecord.for_each( Inc() ); cout << "Enter the index of the element you want to increment :"
<< endl;
int index ;
cin >> index;
if ( myRecord.is_valid_index( index ) )
myRecord.apply( Inc(), index );
else
cout << "Invalid index entered";
return 1;
}
Here is the complete list of operations supported by tek::record. Note that no operation will throw an exception.
template < class T0 ,..., class Ti ><br />tek::record()
Constructs a record of uninitialized elements.
template < class T0 ,..., class Ti ><br />tek::record( const T0& a0 ,..., aj )
Constructs a record with the first j elements initialized.
Example:
tek::record< char, int > myRecord( 'e', 3 ) tek::record< char, int > myRecord( 'w' )
template< int I > <br />return_type& at< I >()
Returns a reference to the element located at the index I. Since the index is given via a template argument, it cannot be determined at runtime. Use the apply function to use a dynamic index.
template< class T > <br />void for_each( T& f )
Applies the functor f to each element of the record.
template< class T > <br />void apply( T& f, const unsigned int x )
Applies the functor f to the element located at the index x. Note: undefined behavior if x is an incorrect index.
static bool is_valid_index( const unsigned int x )
Returns true if x is a valid index to use with the apply function, false otherwise.
template< class B, class T > <br />void for_interface( T& f )
Applies the functor f to the elements whose type is B, or is derived from the base class B.
Those operations are very basic and don't use manipulators. They are provided mainly to test the other records functionalities. I/O operations might be fully supported in the future.
record< ... >::size
Returns the number of types handled by the record.
Example:
typedef tek::record< int, char, double > MyRecordType;
MyRecordType myRecord;
myRecord.size MyRecordType::size
record< ... >::element< I >::type
Returns one of the types of the record given by the index I.
Example:
typedef tek::record< int, char, double > MyRecordType;
MyRecordType::element< 1 >::type
The record implementation is configurable by three macros located in the file tek/config/record_config.h.
#define TEK_RECORD_MAX_PARAMS
Defines the maximum number of types tek::record can handle
-> defined to 20 by default
#define TEK_RECORD_NO_IO
Disables iostream operators support, prevents the inclusion of the <iostream> header
-> not defined by default
#define TEK_RECORD_MERGE_APPLY
Gives access to the merge_apply function. The merge_apply function has the same interface as the apply function but with a different implementation that might lead to a performance gain if the supplied functor does the same processing for some or all elements. It leads to a performance degradation elsewhere. Defining the macro also degrades the performance of the record constructor and increases the record size.
-> not defined by default
If the record type is a dependant name, the member functions and structures that need an explicit template argument must be prefixed by the template keyword.
Example:
template < class T>
void f( T& myRecord )
{
myRecord.template get<1>(); }
Only compilers that implement the two-phase name look-up, such as GCC, will issue an error if the template keyword isn't present. Such compilers parse the template function f, even if f isn't instantiated. While parsing, the compiler doesn't know the type of myRecord and then doesn't know that get is a template function, so you must put the template keyword so that it can correctly disambiguate the < > (which then will be identified as delimiters for a template argument list, and not as a less than / greater than operator). Some compilers, such as Visual C++ 8, look at the template function only when it is instantiated and, at that time, it knows that get is a template member function, so the template keyword isn't needed. The template keyword is easily forgotten, especially if the program that uses a tek::record needs to be portable across several compilers.
That's why each of the member functions and structures has an equivalent in a non-member way so that it is easier to write portable code. For consistency, all member-functions have a non-member counterpart, they have the same name and the same parameter list with the addition of a record parameter at the beginning of the list:
myRecord.get< 0 >();
tek::get< 0 >( myRecord );
myRecord.for_each( myFunctor() );
tek::for_each( myRecord, myFunctor() );
myRecord.apply( myFunctor(), index );
tek::apply( myRecord, myFunctor(), index );
Most of the time, the functor used as an argument for the apply function is a temporary object:
tek::apply( myRecord, myFunctor() );
If so, the const qualifier of the operator() function must not be forgotten:
struct MyFunctor {
template < class T >
void operator()( T& element ) const
{
....
}
}
To simulate argument passing, you can use the constructor of the functor:
struct MyFunctor {
MyFunctor(int arg) : arg_(arg) {}
template < class T >
void operator()( T& element ) const
{
}
int arg_;
}
...
tek::apply( myRecord, myFunctor( 2 ) );
To return a value from the apply function, the functor must derive from the tek::return_type structure, which takes as a template parameter the wanted return type. Every operator() must then return the same type:
struct Inc : public tek:return_type< int > {
template < class T >
int operator()( T& element ) const
{
....
}
}
I measured the dynamic dispatching performance of three kinds of heterogeneous containers:
tek::record - Array of
boost::variant - Classic polymorphic array using a pointer to a base class
Every benchmark is deceptive in some way. In this section, I try to limit this aspect by providing details about how I proceeded.
First of all, since the performance may vary with the number of elements handled by the container, I benchmarked each container with 2 to 20 elements. Each element type is a different class inheriting from a common abstract base class which declares a pure virtual function named foo. Each class implements the foo virtual function. I measured the performance of the call to foo, which gives different statements for each solution:
polymorphism:
container[index]->foo();
boost:variant:
boost::apply_visitor( Visitor(), container[index] );
tek::record:
container.apply( Functor(), index );
For the variant and record solutions, we need to use a functor, respectively called Visitor and Functor in our example, that implements operator() in exactly the same way for both solutions:
template <class />
void operator()(const T& element) const
{
element.T::foo();
}
Note: Because, in our case, passing by reference is faster than passing by value, the parameter is const T& element. However, if we use directly element.foo(), the compiler will probably generate a virtual lookup, element being a reference. We then use the form element.T::foo() so that the call to foo will be statically binded.
For each class, the foo function does a few arithmetic operations. Because the size of foo is very small, it will be systematically inlined, if the dispatch mechanism of the solution allows it.
I tested two configurations:
- The implementation of
foo is different for each class. - The implementation of
foo is the same for half of the classes. The merge_apply function can then apply its optimization.
The index is determined at runtime. Since the call to foo is executed in a loop, I decided to test two kinds of index:
- A stable index that stays the same through all iterations. Note that this stable index is not a constant, it is determined at runtime once and for all.
- A random index that changes in each iteration. Random indexes are prefetched in an array, so that the loop just needs to iterate through that array to obtain a random index for each loop.
We don't only use a random index because the performance of using such an index is greatly dependent on the CPU and its branch prediction unit, and important variations can occur. For example, my machine is a Pentium 4 Prescott that has a 31 stages pipeline. A mistaken branch prediction results in a flush of this pipeline, which considerably degrades performance. A stable index eliminates those variations since the taken branch is always the same. Furthermore a stable index doesn't really favor one solution over another since all three solutions use an unconditional jump with a non-immediate branch target, to implement their dispatch mechanism.
Finally, in order to reduce the number of graphs, I used only two configurations for measuring performance:
- Stable configuration: Stable index + unique implementation of
foo for each class - Unstable configuration: Random index + same implementation of
foo for half of the classes
The benchmarks were performed on a Intel Pentium 4 3Ghz HT, 1 Gb RAM. 2 "platforms" were tested:
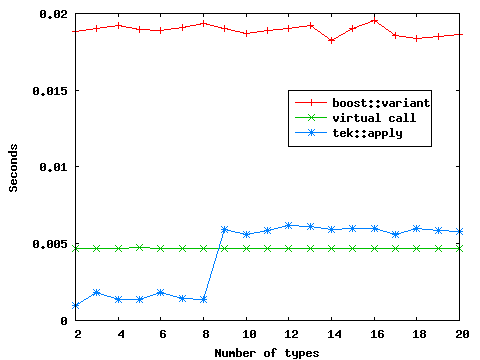
The boost::variant solution is constantly the slowest solution, because Visual C++ isn't able to inline the boost::apply_visitor function. The latter uses a switch statement that generates a jump table, as the tek::record solution, but doesn't adapt the number of cases (see section Pseudo-variadic Behavior Implications). Consequently, it always has 20 cases, which corresponds to the default maximal number of types a boost:variant can handle.
The tek::apply solution is the best until 9 types are handled. At 9 types, the Visual C++ compiler considers that the tek::apply function becomes too big and chooses not to inline it any longer, leading to performance degradation. At that time, virtual calls are the best performing solution by a small margin.

As a general tendency, GCC inlines more aggressively than Visual C++ with the given optimization flags. The boost::variant solution has some performance problem when a few number of types are involved. In fact, as we saw, boost::variant always uses 20 cases switch statement, but the unused cases perform some default processes which have a larger code size than the virtual function foo. So the less the cases are used, the larger the boost::apply_visitor code size will be. Therefore, up to 5 elements, GCC doesn't inline the apply_visitor function. The tek::apply function is always inlined. From 2 to 4 types, GCC doesn't use a jump table to implement the switch case statement, preferring an if then else approach. However, I must say that using this approach leads to an additional optimization, which is a side-effect of having a stable index. Indeed, the tek::apply function is executed in a loop, and when an if then else approach is used, the algorithm looks like this:
for ( ... )
{
if (stable_index == 0)
apply_to_the_first_element
else
apply_to_the_second_element
...
}
However the if condition is invariant since stable_index itself is an invariant. Therefore, GCC is able to transform the code to the following:
if (stable_index == 0)
for ( ... ) {
apply_to_the_first_element
}
else
for ( ... ) {
apply_to_the_second_element
}
...
Even without this optimization that further increases the performance until four types are handled, tek::record is always the best solution here.

As expected, the performances of each solution are unstable with a random index. Because the merge_apply function merges some cases, it can be inline longer than the apply function resulting in a performance improvement over the latter from 8 types to 12 types.

The code generated by GCC for the tek::merge_apply function includes case merging, but doesn't seem to be efficient for my system. It is slower than boost::variant which also allows branch elimination via case merging (because the boost::apply_visitor accepts as an argument the indexed element). The tek::apply function is overall the best here.
Concerning dynamic dispatch performances, tek::record is faster than a container of boost::variant in about every tested context. This is mainly because of some implementation details, as both use a switch case statement, but, intrinsically tek::record should also be a little faster than a container of discriminated unions, because it has a direct access to its elements. Comparing to the virtual call mechanism implemented by the tested compilers, tek::record is faster most of the time, except with Visual C++ on a megamorphic 6 situation. However the benchmarks didn't test every possible situation that may favor one solution over the others. Particularly, virtual functions of large size weren't considered which may sometimes favor basic virtual calls if it prevents inlining. The implementation of virtual calls may also be optimized depending on the compiler, but such optimizations are very scarce in the current world of C++ compilers. However, although these are limited by their static nature, profile-guided compilations allow new optimizations in this area such as virtual call speculation 7. The benchmarks just measured the performance of basic implementations of virtual calls.
tek::record is a fixed size heterogeneous container that provides quite limited functionalities. However, it exhibits the following features simultaneously:
- High performance dynamic dispatch
- Low memory space consumption
- Type identity conservation
[Alexandrescu]: "Modern C++ Design: Generic Programming and Design Patterns Applied", Andrei Alexandrescu - Addison Wesley, 2001
[1] ^ Without considering data structure padding
[2] ^ The visitor pattern
[3] ^ If there are very few cases in the switch, jump tables aren't the fastest implementation any longer: the compiler may use another approach to implement a switch case in this situation.
[4] ^ Some compilers are more or less tolerant towards how contiguous the values must be.
[5] ^ For instance, if the index, used to access an element in some array, is computed earlier in such a way that it will be mathematically a valid index under any circumstance, the compiler can then apply bounds checking elimination and use the index directly: it doesn't affect the program's correctness.
[6] ^ Megamorphism = polymorphism with a high number of types.
[7] ^ Virtual call speculation is one of the profile guided optimizations proposed by Visual C++ 8.
- 24-02-2008:
- License change from GPL to CPOL
- [Article] small explanation added about the inlining policy of Visual C++ ( section Platform Visual C++ )
- [Article] correction in the
get_type code ( section Typelist ) - [Article] correction in the functor code to illustrate the
return_type feature ( section Functor Definition )
- 30-01-2008: Initial version
