Introduction
Changing a LINQ expression dynamically (at runtime) depending on the user’s input is one of the problems that is often discussed in forums and blogs. I know at least three solutions, proposed by Tomas Petricek (http://tomasp.net/blog/linq-expand.aspx), Joe Albahari (http://www.albahari.com/nutshell/predicatebuilder.html), and implemented in the DynamicQuery MS sample. In this article, I want to show how rewrite rules can be defined as lambda expressions and used to transform expressions (queries). This technique may provide the following benefits:
- It is applicable to any part of any expression. You can change dynamically, for instance, where conditions, sorting, or grouping criteria.
- Rewrite rules give a high-level definition of transformations and do not employ any implementation details of expressions. You don’t need to know how and why flags like “IsLifted” must be set in a predicate you want to build. The rewriting engine itself (the classes in the library that accompanies the article), processes expressions, of course, on the implementation level.
Rewrite rules, being themselves lambda expressions, are subject to syntax and type checking. If you get no compiler errors, you can be sure that the transformation result will be a well formed expression consistent with respect to types.
Background
Rewrite rules is an interesting field with a solid mathematical background. Rewriting is typically used to reduce expressions to a canonical form to check their equality induced by a theory, expressed by a set of equations. (See, for instance, http://en.wikipedia.org/wiki/Knuth-Bendix_completion_algorithm.)
Transforming LINQ expressions can hardly be seen as an equation theory and a mathematical background is not needed ( :-( ) neither to understand this article nor to use rewriting in the case described here.
Demo Program
The demo program is a Windows Forms (VS 2008 Express) application that reads the Customers table from the Northwind database. The controls on the form modify where clause conditions and orderBy key selectors.
The unmodified query in the program is as follows, so you can see what it reads:
var q = from ext in
( from c in ctx.Customers
where dummyFilter( c )
select new CustomerExt{
OrdersNo = c.Orders.Count(), Address = c.Address,
City = c.City, CompanyName = c.CompanyName,
Country = c.Country, CustomerID = c.CustomerID,
Orders = c.Orders, Region = c.Region
} )
orderby dummySelector( ext )
select ext
;
Controls on the Form
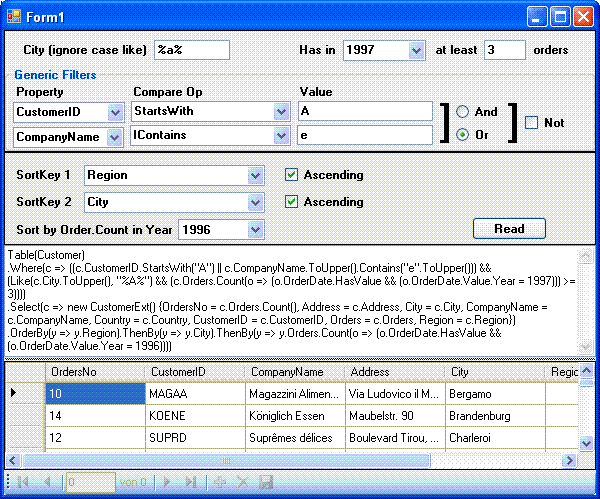
I have put all the controls on one form and the allowed width for pictures is only 600 pixels, so we’ll inspect the controls detailed to avoid a confusion. The form consists of two panels, a textbox and a grid.
In the topmost panel, the user can define conditions that are dynamically inserted into the Where clause. The two control groups in the first row

use the following hard coded expressions:
c => SqlMethods.Like( c.City.ToUpper(), [user_input_to_upper])
and
c => c.Orders.Count( o => o.OrderDate.HasValue &&
o.OrderDate.Value.Year = [year]) >= [number])
where the words in square brackets represent the content of the input fields.
The two rows in the group box “Generic Filters” define simple generic binary conditions. The user can select a property name, a compare operation, and give a value to compare with.

These two conditions can be combined with AND or OR and the result can be negated. The settings in the picture result in this condition:
c => c.CustomerID.StartsWith("A")
|| c.CompanyName.ToUpper().Contains("e".ToUpper())
The first two conditions from the topmost row are always attached to the generic ones with the AND operation. If some input fields are not filled, the corresponding condition doesn’t apply.
The next panel defines the OrderBy keys.

The first two rows define simple keys based on properties. The comboboxes list all the applicable properties. The effect of the first two rows shown in the picture is the following query sub-expression:
.OrderBy(e => e.Region).ThenBy(y => y.City)
The last row is there to show that any (valid) expression, even with parameters, can be used as a key selector in OrderBy/ThenBy. The expression behind this row is:
y => y.Orders.Count(o => o.OrderDate.HasValue
&& o.OrderDate.Value.Year = 1996)
The textbox in the middle of the form displays the query expression after all modifications apply.
The query results are shown in the grid on the bottom.
Download
The download contains a library named Rewrite and the demo application.
The library defines two namespaces: Rewrite and RewriteSql. The namespace Rewrite contains general purpose rewriting classes that can be used to modify any kind of expression. The second namespace RewriteSql uses the first one and contains classes that transform the OrderBy and Where clauses of a LINQ to SQL query. These classes are not specific to the demo application and can handle any query.
If you want to use rewriting in your application to modify Where and/or OrderBy portions of queries, you need only to reference the library and follow the patterns in the demo app.
The demo application needs the Northwind database to be installed. Change the property DataAccess.TheConnectString or the settings it references.
An Attempt that Fails but Helps to Reinvent Rewrite Rules
Let’s start with a simple and rather inflexible program:
private IList<customer> GetCustomers( string city){
using( NWindDataContext ctx
= new NWindDataContext( DataAccess.TheConnectString ) ) {
var q = ctx.Customers.Where( x => x.City.StartsWith( city));
return q.ToList();
}
}
There is one parameter that controls the selection. Can we go on and parameterize, for instance, the compare operation? So that we can pass EndWith(), IsEqual(), or Like() to replace StartsWith(). Let’s try and change the program as follows:
private IList<Customer> GetCustomers( string city, Func<string,string,bool> comp){
using( NWindDataContext ctx
= new NWindDataContext( DataAccess.TheConnectString ) ) {
var q = ctx.Customers.Where( x => comp( x.City, city));
return q.ToList();
}
}
It can be called like:
Func<string, string, bool> stw = ( s1, s2 ) => s1.StartsWith( s2 );
IList<Customer> lst = this.GetCustomers( "Lo", stw);
The program compiles, but fires a runtime exception because it can’t translate the query. The query expression is:
Table(Customer).Where(
x => Invoke(value(RewriteDemo.Form1+<>c__DisplayClass1).comp,
x.City,
value(RewriteDemo.Form1+<>c__DisplayClass1).city))
and the method name of comp is:
?comp.Method.Name
"<CallerMwthod>b__3"
No wonder that the program fails. This is the internal name of the anonymous delegate assigned to stw in the caller, and though it merely calls StartsWith(), its name is unknown to the LINQ to Sql query provider. It is not possible for the provider to look into a compiled delegate and see what it consists of.
This prompts that we can pass as parameter something that is more transparent than a compiled delegate – an expression. Here is the next version of the program:
private IList<Customer> GetCustomers( string city,
Expression<Func<string,string,bool>> rhs){
using( NWindDataContext ctx = new NWindDataContext(
DataAccess.TheConnectString ) ) {
Func<string, string, bool> p = null;
var q = ctx.Customers.Where( x => p( x.City, city));
Expression<Func<string, string, bool>> lhs = ( s1, s2 ) => p( s1, s2 );
Rule r = new Rule( lhs, rhs);
Expression e = Replace( q.Expression, r);
var qq = q.Provider.CreateQuery<Customer>( e);
return qq.ToList();
}
}
It can be called so:
Expression<Func<string, string, bool>> stw =
( s1, s2 ) => s1.StartsWith( s2 );
IList<Customer> lst = this.GetCustomers( "Lo", stw);
What should the hypothetical method Replace() do to make us happy? It takes an expression to transform and a pair of lambda expressions (the class Rule is simply a pair). It must scan the target for a sub-expression that matches the first lambda expression and replace it for the second lambda expression. That’s all. Congratulations! We have reinvented rewriting.
What is crucially important: the method Replace() needs to know nothing about Customers, specific compare operations applicable to strings, about the Where() method, or even about LINQ. It must only know how expressions in C# are built internally and how to manipulate them. And since it encapsulates this knowledge, we need not care about the internal details of expressions when we use the method. There is no Replace() method in the library, but the static method SimpleRweriter.ApplyOnce() makes exactly what is described here.
Replacing one delegate is nice, but we need much more to make queries flexible. A query can, of course, have several “extension points” denoted above in the program by the dummy delegate p. They will be processed independently as long as the dummies have different names and can be thus distinguished by the first components of the rules.
With the same mechanism, it is possible to replace any part of an expression. Property getters can be replaced. We can take an auxiliary expression p1 || p2 and replace p1 and p2 to get a conjunction and then replace a dummy delegate in Where( x => dummy( x)) for the conjunction, etc. Actually, how to do transformations of this kind is what the article is about.
But first, we should look at rewriting more closely.
Rewrite Rules
The intent of the transformation applied above will be even more obvious if we write both lambda expressions in the form traditional for rewrite rules (unfortunately, not acceptable by C# even in 3.0 :)):
p( s1, s2) --> s1.StartsWith( s2 )
This is a “rewrite rule”. The expression before the arrow is called the left-hand-side (lhs) of the rule; the expression following the arrow is its right-hand-side (rhs). The meaning of the rule can be expressed informally this way: “Check all sub-expressions of the expression you want to transform. If you find a sub-expression that matches the lhs of a rule, replace it for the rhs of this rule, substituting the variables in the rhs for the values they get when the lhs is matched against the source expression.”
The lhs of a rule is a pattern to be found in the source expression. The rhs replaces the found sub-expression.
If a rule is written in this short form, it still lacks additional information to distinguish variables and to check their types. Thus, the way rules can be defined in C# (as two lambda expressions) is not that much redundant. One restriction must hold: both lambda expressions must have the same signature, that is, the same number and the same types of parameters (variables). Only then can they be used as one rewrite rule. The names of the parameters may differ, but for the sake of readability, it is better to denote the same “things” with the same names in both expressions.
Theoretically, any algorithm can be defined with the help of rewrite rules. In this article, we strive for a more moderate goal. In contrast to the common usage pattern of rewrite rules, we will employ a specific rewriting strategy. Each rule is tried only once and must succeed at some sub-expression (in some cases, one of the alternative rules must succeed). When rewrite rules are used as a general computation engine, commonly used strategies apply a set of rules in a bottom-up or top-down fashion, as long as any of the rules succeed.
Using the Libraries
In this article, I do not describe the implementation of the rewrite engine itself. Its public classes used from outside the library are Rule and SimpleRewriter. The class Rule is simply a pair of lambda expressions. The constructor ensures that both expressions are not null and have the same signature. The static method Create() is a kind of a constructor that allows in many cases to write lambda expressions immediately as parameters and hence avoid writing their types explicitly.
The constructor of the class SimpleRewriter accepts an expression. This is the expression that is to be transformed. The instance method ApplyOnce() takes a rule as a parameter, tries to apply it to the expression, and returns true on success. The resulted expression can be accessed through the read only property Expression.
Here is a hypothetical program (sorry, I haven’t really tested it) that makes some well known arithmetical transformations. It shows how to use the classes and gives some feeling about what rewrite rules are.
public Expression Test( Expression ex){
Expression<Func<int,int,int,int>> lhs1 = (x,y,z) => (x + y) * z;
Expression<Func<int,int,int,int>> rhs1 = (x,y,z) => x * z + y * z;
Rule r1 = new Rule( lhs1, rhs1);
SimpleRewriter rwr = new SimpleRewriter( ex);
while( rwr.ApplyOnce( r1))
;
return rwr.Expression;
}
Provided with the argument:
int a = 0;
int b = 0;
Expression<Func<int>> expr = () => (a + 3) * 1 * b;
The test program applies twice the rule and returns a * 1 * b + 3 * 1 * b.
Other rules may be added:
Expression<Func<int,int >> lhs2 = x => x * 1;
Expression<Func<int,int >> rhs2 = x => x;
Rule r2 = new Rule( lhs2, rhs2);
Expression<Func<int,int >> lhs3 = x => x * 0;
Expression<Func<int,int >> rhs3 = x => 0;
Rule r3 = new Rule( lhs3, rhs3);
The loop must be changed:
while( rwr.ApplyOnce( r1)
|| rwr.ApplyOnce( r2)
|| rwr.ApplyOnce( r3)
)
;
Applied to the same source expression, the test program will now return a * b + 3 * b. Note that though the variable b has a zero value, the rule x*0 --> 0 must not and doesn’t apply. Variable values are never considered by transformations. Note also that the method ApplyOnce() doesn’t know that multiplication is commutative. The rules:
must be added explicitly, if needed.
Now a few words should be told about applying a rule. Not about how ApplyOnce() is implemented, but about what it must do. The first step is matching the lhs of a rule against a (sub-)expression. Essentially, matching is something like equality check, but handles variables differently. The first point, that is sometimes the source of confusion, is that in this context, only the lambda parameters of the lhs and of the rhs are variables. None of the program variables that occur in the target expression or in the rule are treated as variables. Both the parameters of lambda expressions in the target and the parameters of inner lambdas in the rule are not variables either. They all are treated as constants. Matching (if successful) results in a substitution. A substitution is a mapping variable-->expression. To apply a substitution to an expression means to substitute the variables in the expression for expressions the variables are mapped on. An lhs matches an expression if there is a substitution that makes the lhs literally equal to the expression.
Here is an example. The lhs:
(x + y) * z
matches the expression:
(a*1 + 3*1) * b
due to the substitution:
x --> a*1
y --> 3*1
z --> b
If a substitution was found (matching succeeds), the second step in applying a rule is to apply the substitution to the rhs. Continuing the example and remembering that the rhs was x * z + y * z, we obtain a*1 * b + 3*1 * b. The final step is to replace the expression that matches the lhs for this expression.
The following propositions might be interesting. If matching is successful, then all variables in the lhs are mapped by the resulting substitution. Since the rhs of the same rule has the same variables, all of them are replaced and variables never get substituted into the target expression.
I hope that it is clear now what and how the core rewriting method must do and how it can be implemented. The method ApplyOnce() and the methods it calls are based on the visitor pattern (no wonder) and their sources are included in the demo project.
In the rest of the article, we will look at how rewriting can be used to build and modify query expressions. Because of this, I’ll describe the usage of the libraries and the methods that are specific to query rewriting, and I’ll stop digging down into the libraries when calls to ApplyOnce() are reached.
Data Access Method
The program that reads data is listed below. It is straightforward and differs from a typical LINQ to SQL data access method only through two additional parameters and two calls that handle these parameters.
public static List<CustomerExt> GetCustomersSorted(
Expression<Func<Customer, bool>> filter,
Expression<Func<IQueryable<CustomerExt>,
IOrderedQueryable<CustomerExt>>> orderByClause)
{
using( NWindDataContext ctx = new NWindDataContext( TheConnectString ) ) {
Func<Customer, bool> dummyFilter = null;
Func<CustomerExt, object> dummySelector = null;
var q = from ext in
( from c in ctx.Customers
where dummyFilter( c )
select new CustomerExt{
OrdersNo = c.Orders.Count(), Address = c.Address,
City = c.City, CompanyName = c.CompanyName,
Country = c.Country, CustomerID = c.CustomerID,
Orders = c.Orders, Region = c.Region
} )
orderby dummySelector( ext )
select ext;
var e1 = WhereRewriter.Rewrite( q.Expression, x => dummyFilter( x ), filter );
var e2 = OrderByRewriter.Rewrite( e1, x => dummySelector( x ), orderByClause );
return WhereRewriter.RecreateQuery( q, e2 ).ToList();
}
}
You have surely noticed two suspicious delegates used in the query: dummyFilter and dummySelector, and you already have an idea what they are there for. You are right – they simply mark the places where dynamically built query portions must be inserted. The only requirement to these dummies is that they must have types that correspond to the place where they occur (so that the query compiles). The compiler requires also that they must get a value before they are used. A null value fits as long as you don’t try to compile/execute the query. The query will be executed when .ToList() is called in the return statement and before this happens, we will replace the dummies.
The parameters filter and oredByClause give what for to replace the dummies. They both are lambda expressions. The type of the filtering lambda expression is exactly the same as the type of the dummyFilter delegate. The type of the second lambda expression is based on the same element type as the dummySelector (the CustomerExt type) but must correspond to the type of the whole orderby section of the query. It embraces, so to say, the keyword orderby. The reason for different typing is obvious: while any filter can be expressed as a single Boolean expression, sorting can be done by more than one key and so is more than one key selector. In the first case, we use dummyFilter as a marker and replace only it. In the second case, we use dummySelector as a marker and replace the whole OrderBy clause.
Valid parameter values are, for example:
c => c.City == "London" || c.City == "Lisboa"
ce => ce.OrderBy( ce.Country).ThenBy( ce.Region)
Each parameter can be null, meaning “no filter” and “no sorting”, respectively. The method WhereRewriter.RecreateQuery() used in the program is a little wrapper that allows not to write query types explicitly. First, we’ll look at the methods that rewrite where and orderby sections (WhereRewriter.Rewrite and OrderByRewriter.Rewrite, respectively), and then we’ll discuss how rewriting can help to dynamically build the query portions that must be inserted.
Modifying the Where Clause
The method WhereRewriter.Rewrite() looks as follows (slightly simplified):
public static Expression Rewrite<tentity>(
Expression expr,
Expression<func<tentity, >> dummyPred,
Expression<func<tentity, >> filter )
where TQuery: IQueryable
{
SimpleRewriter rwr = new SimpleRewriter( expr);
if( filter == null){
Func<tentity, > p = null;
rwr.ApplyOnce( FilterBuilder.FilterRule( dummyPred, z => p( z ) ) );
rwr.ApplyOnce(
Rule.Create<iqueryable<tentity >,IQueryable<tentity >>(
x => x.Where( y => p( y ) ),
x => x ) );
} else {
rwr.ApplyOnce( FilterBuilder.FilterRule( dummyPred, filter ) );
}
return rwr.Expression;
}
The class WhereRewriter is not specific to the demo, it can modify any call to Where(). The type parameter TEntity must be equal to the TSource parameter of the targeted Where().
The method takes the following three parameters:
expr is the query expression to be modified. It contains a call to Where() with a dummy predicate as parameter. In the demo, the dummy predicate is the local variable dummyFilter defined in the caller.dummyPred is a lambda expression of the form x => d( x), where d is the dummy predicate.filter is a lambda expression that gives the condition to be inserted.
If the third parameter is not null, the processing is quite simple: the second and the third parameters are exactly the lhs and the rhs of the rule that must be applied.
If the third parameter is null, the call to Where() must be removed. This transformation can be done with the following rule:
Rule r = Rule.Create<IQueryable<TEntity>,IQueryable<TEntity>>(
x => x.Where( y => dummyFilter( y)), x => x);
But if written this way, the rule can’t compile – the variable dummyFilter is defined in a different scope. Here I want to warn for a typical pitfall. The solution that seems to be obvious – to pass the dummy predicate as an additional parameter and use this parameter in the rule – doesn’t work. The rule will compile, but will not apply. The reason is that this new parameter will still be a different variable that gets the value but not the “identity” of the dummy predicate defined in the caller. If I’m not mistaken, it was possible in Algol 68 to describe a parameter not only as “by value” or “by reference” but also as “by name”. But C# is not Algol 68 (fortunately :)).
The following workaround seems to be a general solution. We define all the rules we need using an absolutely new variable (named p in the program) instead of the one defined in the caller (dummyFilter in the demo). Then we have two possibilities:
- replace
p for dummyFilter in all rules, or alternatively - replace
dummyFilter for p in the target expression (this is done in the demo).
The corresponding rules are:
p( x) --> dummyFilter( x) // case (i)
dummyFilter( x) --> p( x) // case (ii)
These rules also reference the out of scope variable, but we already have the needed lambda expression – it is passed as the parameter dummyPred.
Creating Where Conditions
Now we’ll look at how rewriting helps to create where conditions dynamically. In general, a condition consists of primitive predicates combined together with the help of AND, OR, NOT, etc. The demo illustrates two ways to create primitive predicates:
- hard coded expressions;
- generated expressions that follow a generic pattern.
Hard Coded Predicates
Here is an example of a hard coded primitive predicate:
public static Expression<Func<Customer, bool>>
MakeCityFilter( string value ) {
if( string.IsNullOrEmpty( value ) )
return null;
value = value.ToUpper();
Expression<Func<Customer, bool>> expr =
c => SqlMethods.Like( c.City.ToUpper(), value );
expr = SimpleRewriter.ApplyOnce(
expr,
Rule.Create( () => value,
EvaluateLiteral.CreateRhs( value ) ) );
return expr;
}
There is not much to comment. The call to the static method ApplyOnce() replaces the reference to the variable value for its value. This is made only to enhance the readability of the expression: the variable captures results in hardly readable expressions. If the variable has the value “%a%”, then before rewriting, the expression looks like:
c => Like(c.City.ToUpper(),
value(RewriteDemo.UserInput+<>c__DisplayClass4).value)
and after rewriting, it reads like:
c => Like(c.City.ToUpper(), "%A%")
Hard coded predicates are checked by the compiler. This is a great advantage. The disadvantage of hard coded predicates is that they are hard coded (must exist already in the source code).
The method EvaluateLiteral.CreateRhs() used in the program looks as follows:
public static Expression<Func<VType>> CreateRhs<VType>( VType value ) {
ConstantExpression cex = Expression.Constant( value );
return (Expression<Func<VType>>)Expression.Lambda( cex );
}
This little function deserves more attention. Its purpose is obvious: called with the argument, for instance, “LOND%”, it returns the lambda expression () => “LOND%”. To build the result, it uses the implementation level – the constructor-like methods of the class Expression. Here we reach the limits of rewriting. More on this at the end of the article.
Generic Predicates
Often primitive filters simply compare a property value with the user’s input. So the idea is to prepare a generic binary predicate (filter) of the following form: CompareOp( entity.Prop, value) and replace the dummy property and the dummy compare operation for the specific members requested by the UI.
The generic pattern is encapsulated by the class PropertyGenericBinFilter. Let’s see this class.
public class PropertyGenericBinFilter<TEntity,TValue>:
IPropertyGenericBinFilter<TEntity> {
private Expression<Func<TEntity, bool>> _expr;
private Expression<Func<TEntity, TValue>> _propertyLhs;
private Expression<Func<TValue, TValue, bool>> _compareOpLhs;
private Expression<Func<TValue>> _valueLhs;
public PropertyGenericBinFilter() {
Func<TValue, TValue, bool> op = null;
Func<TEntity, TValue> prop = null;
TValue value = default( TValue );
_compareOpLhs = ( x, y ) => op( x, y );
_propertyLhs = e => prop( e );
_valueLhs = () => value;
_expr = e => op( prop( e ), value );
}
#region IPropertyGenericBinFilter<TEntity> Members
public Expression<Func<TEntity, bool>> Expression {
get { return _expr; }
}
public void RewriteGetter( LambdaExpression rhs ) {
_expr = SimpleRewriter.ApplyOnce( _expr,
Rule.Create( _propertyLhs,
(Expression<Func<TEntity, TValue>>)rhs ) );
}
public LambdaExpression CompareOpLhs {
get { return _compareOpLhs; }
}
public LambdaExpression ValueLhs {
get { return _valueLhs; }
}
public Type PropertyType {
get { return typeof( TValue ); }
}
#endregion
}
The class has two type parameters – the entity type TEntity and the property type TValue.
The constructor creates four expressions – the generic pattern and three expressions that can be used as left-hand-sides to replace dummies. Immediately after an instance is created, the method RewriteGetter() must be called. It replaces the dummy property getter prop for a real one (could have been done in the constructor also). The instance is cached in a dictionary. When the real compare operation and the value to compare with are known, the pattern is rewritten and gets its final form that can be inserted into the query.
The static method Create of the class GenericBinFilter controls the actions needed to create an instance of PropertyGenericBinFilter from cache or creates a new one. Note that the static methods of the Expression class are used to create the rhs to replace the dummy getter. The class GenericBinFilter has one type parameter – TEntity. The text of the method Create() follows.
public static Expression<Func<TEntity, bool>> Create( string propertyName,
string compareOp, object value )
{
IPropertyGenericBinFilter<TEntity> propFilter;
if( !_cache.TryGetValue( propertyName, out propFilter ) ) {
PropertyInfo pi = typeof( TEntity ).GetProperty( propertyName );
if( pi == null )
return null;
Type[] genTypes = { typeof(TEntity), pi.PropertyType};
Type filterType = typeof( PropertyGenericBinFilter<,> )
.MakeGenericType( genTypes );
propFilter = (IPropertyGenericBinFilter<TEntity>)
Activator.CreateInstance( filterType );
ParameterExpression p = Expression.Parameter( typeof( TEntity ), "e" );
LambdaExpression propRhs = Expression.Lambda(
Expression.MakeMemberAccess( p, pi ),
p );
propFilter.RewriteGetter( propRhs );
_cache.Add( propertyName, propFilter );
}
SimpleRewriter rwr = new SimpleRewriter( propFilter.Expression );
LambdaExpression opRhs = CompareOpDecoder.Decode( propFilter.PropertyType,
compareOp );
rwr.ApplyOnce( new Rule( propFilter.CompareOpLhs, opRhs ) );
rwr.ApplyOnce( new Rule( propFilter.ValueLhs,
EvaluateLiteral.CreateRhs( propFilter.PropertyType, value ) ) );
return (Expression<Func<TEntity, bool>>)rwr.Expression;
}
The interface IPropertyGenericBinFilter defines a common “view” on all PropertyGenericBinFilter objects with the same TEntity and different value types.
Note that replacing of the variable value for a constant with the same value not only enhances readability in this case. If a where condition contains two (or more) primitive filters that originate from the same cached instance, for instance:
x.City == "London" || x.City == "Lisboa"
then both primitive filters will actually reference the same instance of the variable value that can’t have two different values “London” and “Lisboa” at the same time.
The static method CompareOpDecoder.Decode() decodes strings into lambdas that can insert the encoded operations (if used as the rhs of a rule). If the method gets, for instance, parameters typeof( string) and “StartsWith”, it returns the following expression:
( x, y ) => x.StartsWith( y )
The expressions are selected from static nested dictionaries keyed by type codes and strings that denote compare operations. These dictionaries are common for all entity types (for the whole application). A piece of code that fills the dictionaries follows. It is clear that you can fill them with any key/value pair you need in your application.
public static class CompareOpDecoder {
public static Dictionary<TypeCode, Dictionary<string, LambdaExpression>>
CompareOpDictionary;
static CompareOpDecoder() {
CompareOpDictionary =
new Dictionary<TypeCode, Dictionary<string, LambdaExpression>>();
#region string compare
Dictionary<string, LambdaExpression> stringOps
= new Dictionary<string, LambdaExpression>
( StringComparer.InvariantCultureIgnoreCase );
stringOps.AddStringPredicate( "==", ( x, y ) => x == y );
stringOps.AddStringPredicate( "!=", ( x, y ) => x != y );
stringOps.AddStringPredicate( "StartsWith", ( x, y ) => x.StartsWith( y ) );
stringOps.AddStringPredicate( "EndsWith", ( x, y ) => x.EndsWith( y ) );
stringOps.AddStringPredicate( "Contains", ( x, y ) => x.Contains( y ) );
stringOps.AddStringPredicate( "IStartsWith",
( x, y ) => x.ToUpper().StartsWith( y.ToUpper() ) );
stringOps.AddStringPredicate( "IEndsWith",
( x, y ) => x.ToUpper().EndsWith( y.ToUpper() ) );
stringOps.AddStringPredicate( "IContains",
( x, y ) => x.ToUpper().Contains( y.ToUpper() ) );
stringOps.AddStringPredicate( "Like", ( x, y ) => SqlMethods.Like( x, y ) );
stringOps.AddStringPredicate( "ILike",
( x, y ) => SqlMethods.Like( x.ToUpper(),
y.ToUpper() ) );
CompareOpDictionary.Add( TypeCode.String, stringOps );
#endregion
The function AddStringPredicate() is a little helper function. It prescribes the type of the arguments and so it’s not needed to declare the type of each expression explicitly.
private static void AddStringPredicate(
this Dictionary<string, LambdaExpression> dict,
string opName,
Expression<Func<string, string, bool>> expr )
{
dict.Add( opName, expr );
}
The method MakeCityFilter() used above to illustrate hard coded predicates could have been written in the following way if we prefer to build the predicate dynamically:
public static Expression<Func<Customer, bool>> MakeCityFilter( string value ) {
if( string.IsNullOrEmpty( value ) )
return null;
return GenericBinFilter<Customer>.Create( "City", "ILike", value );
}
Combining Predicates
Static methods of the class FilterBuilder combine predicates into more complex ones with the help of Boolean operations. Let’s look at the method And().
public static Expression<Func<TEntity, bool>> And<TEntity>(
params Expression<Func<TEntity, bool>>[] args ) {
Func<TEntity, bool> p1 = null;
Func<TEntity, bool> p2 = null;
Expression<Func<TEntity, bool>> expr = e => p1( e);
SimpleRewriter rwr = new SimpleRewriter( expr );
bool noArgs = true;
foreach( var arg in args.Where( y => y != null ) ) {
noArgs = false;
rwr.ApplyOnce( FilterRule<TEntity>( e => p1(e), e => p2(e) && p1(e)));
rwr.ApplyOnce( FilterRule( e => p2( e), arg));
}
if( noArgs )
return null;
Expression<Func<bool, TEntity, bool>> lhs = ( x, e ) => x && p1( e );
Expression<Func<bool, TEntity, bool>> rhs = ( x, e ) => x;
rwr.ApplyOnce( new Rule( lhs, rhs ) );
return (Expression<Func<TEntity, bool>>)rwr.Expression;
}
The method accepts a sequence of predicates and returns a conjunction of all non-null ones or null, if there are none. The result expression initially contains only p1. For each non-null argument, p1 is replaced for p2 && p1 and immediately after this, p2 is replaced for the current argument.
This is the trace of rewriting steps (assuming all arguments are not null):
e => p1( e)
e => p2( e) && p1( e)
e => arg1( e) && p1( e)
e => arg1( e) && (p2( e) && p1( e))
e => arg1( e) && (arg2( e) && p1( e))
e => arg1( e) && (arg2( e) && (p2( e) && p1( e)))
e => arg1( e) && (arg2( e) && (arg3( e) && p1( e)))
. . .
At the end, if there were non-null arguments, the expression looks as follows:
arg1 && (arg2 && (arg3 ... && ( argN && p1) ... ))
The rule x && p1 --> x removes p1 from the expression, effectively producing the needed result.
Modifying an OrderBy Section
The method OrderByRewriter.Rewrite() is much like WhereRewriter.Rewrite(). It replaces a call to OrderBy() with a dummy delegate for the body of the expression passed as its third argument. It is more interesting to look at how this expression is built.
Creating an OrderBy Expression
The core class here is OrderByItem. An instance of the class saves a key selector expression and an ascending/descending flag. Its properties OrderByExpr and ThenByExpr return expressions based on the saved information. The text of the OrderByExpr property follows:
public Expression<Func<IQueryable<TEntity>,IOrderedQueryable<TEntity>>>
OrderByExpr {
get {
Func<TEntity, TKey> dummy = null;
Expression<Func<IQueryable<TEntity>, IOrderedQueryable<TEntity>>> ret;
if( _ascending )
ret = x => x.OrderBy( y => dummy( y));
else
ret = x => x.OrderByDescending( y => dummy( y));
return SimpleRewriter.ApplyOnce( ret,
Rule.Create( y => dummy( y ), _keySelector ) );
}
}
The property is simple and hardly needs comments. The functions OrderBy/ThenBy have two arguments – a sequence to sort and a key selector delegate that defines an order of the sequence items. Due to currying, the properties OrderByExpr and ThenByExpr return expressions with only one argument since the saved delegate is already embedded into them.
The class OrderByItem has two constructors. The first one takes a key selector expression and a Boolean, and is used to create OrderBy/ThenBy calls based on hard coded selector keys. The second one takes a PropertyInfo and a boolean, and creates OrderBy/ThenBy calls based on a generic selector key expression.
Hard Coded Selector Keys
A few lines are enough to create an OrdrByItem instance when a key selector is known at compile time. An arbitrary complex expression with parameters can be used as the selector. Here is a piece of code from the demo app:
int year;
if( int.TryParse( this.cboSortYear.Text, out year ) ) {
Expression<Func<CustomerExt, int>> expr3 =
z => z.Orders.Count( o => o.OrderDate.HasValue
&& o.OrderDate.Value.Year == year );
expr3 = SimpleRewriter.ApplyOnce( expr3,
Rewrite.Rule.Create( () => year,
EvaluateLiteral.CreateRhs( year ) ) );
skey3 = new OrderByItem<CustomerExt, int>(
expr3,
true );
}
As with hard coded filters above, rewriting is used here only to improve readability. You will agree, I hope, that "z => z.Orders.Count(o => (o.OrderDate.HasValue && (o.OrderDate.Value.Year = 1997)))" reads better, than "z => z.Orders.Count(o => (o.OrderDate.HasValue && (o.OrderDate.Value.Year = value(RewriteDemo.Form1+<>c__DisplayClass2).year)))".
Generic Selector Keys
The most of the practically used key selectors are simply properties of the sorted items. These simple selectors are built by the constructor that accepts PropertyInfo as the first parameter. The constructor uses static methods of the Expression class. Its text follows:
public OrderByItem( PropertyInfo pi, bool ascending ) {
_ascending = ascending;
ParameterExpression p = Expression.Parameter( typeof( TEntity ), "x" );
_keySelector = (Expression<Func<TEntity, TKey>>)Expression.Lambda(
Expression.MakeMemberAccess( p, pi ),
p );
}
The class OrderByItem has two type parameters: the type of the sequence elements and the type returned by the key selector (these are exactly the type parameters of the function OrderBy()). The first one is known at compile time. When an arbitrary property can be requested, it’s not possible to call the proper constructor statically (the second type is not known at compile time). The method BuildGeneric() calls the needed constructor dynamically:
public static IOrderByItem<TEntity>BuildGeneric(
string propName, bool ascending )
{
PropertyInfo pi = typeof( TEntity ).GetProperty( propName );
if( pi == null )
throw new ArgumentOutOfRangeException(
"propName",
string.Format( "Property '{0}' not found in type '{1}'.",
propName, typeof( TEntity ).Name ) );
Type[] genTypes = { typeof( TEntity ), pi.PropertyType };
Type type = typeof( OrderByItem<,> ).MakeGenericType( genTypes );
return (IOrderByItem<TEntity>)
Activator.CreateInstance( type, pi, ascending );
}
Building an OrderBy Clause
The method OrderByBuilder.MakeOrderByClause() is much like FilterBuilder.And(), but joins the expressions with a function application instead of AND. Here is the text and some comments follow.
public static Expression<Func<IQueryable<TEntity>,IOrderedQueryable<TEntity>>>
MakeOrderByClause( params IOrderByItem<TEntity>[] args )
{
bool firstItem = true;
Func<IQueryable<TEntity>, IOrderedQueryable<TEntity>> oby = null;
Func<IOrderedQueryable<TEntity>, IOrderedQueryable<TEntity>> thby1 = null;
Func<IOrderedQueryable<TEntity>, IOrderedQueryable<TEntity>> thby2 = null;
Expression<Func<IOrderedQueryable<TEntity>, IOrderedQueryable<TEntity>>>
lhs1 = x => thby1( x );
Expression<Func<IOrderedQueryable<TEntity>, IOrderedQueryable<TEntity>>>
rhs1 = x => thby1( thby2( x ) );
Expression<Func<IQueryable<TEntity>, IOrderedQueryable<TEntity>>>
ret = x => thby1( oby( x ) );
SimpleRewriter rwr = new SimpleRewriter( ret );
foreach( var arg in args.Where( a => a != null ) ) {
if( firstItem ) {
firstItem = false;
rwr.ApplyOnce( Rule.Create( x => oby( x ), arg.OrderByExpr ) );
} else {
rwr.ApplyOnce( new Rule( lhs1, rhs1 ) );
rwr.ApplyOnce( Rule.Create( x => thby2( x ), arg.ThenByExpr ) );
}
}
if( firstItem )
return null;
rwr.ApplyOnce( Rule.Create( lhs1, x => x ) );
return (Expression<Func<IQueryable<TEntity>,
IOrderedQueryable<TEntity>>>)
rwr.Expression;
}
The method takes a sequence of IOrderByItem objects as parameters (actually, objects of type OrderByItem with different type parameters in the second position – there are no other types that implement IOrderByItem).
The expression to be returned at the end is initialized to x => thby1( oby( x ) ). The function from the OrderByExpr property of the first non-null parameter replaces the dummy delegate oby. So the expression changes to x => thby1( f1( x ) ), where f1 is the body of the lambda expression returned by arg[ 0].OrderByExpr. As you will remember, the body has one argument due to currying of OrderBy/OrderByDescending.
For each next non-null argument, the dummy delegate thby1 is replaced for thby1( thby2()). The expression becomes x => thby1( thby2( f1( x ) ) ). Then, thby2 is replaced for the body of arg[ i].ThenByExpr producing x => thby1( f2( f1( x ) ) ). At the end, the expression looks like x => thby1( fN( ... f2( f1( x )) ... )). The call to thby1 is removed and the result is exactly what we need.
Hard Coded vs. Dynamically Generated Expressions
You might have noted that rewriting can rearrange nodes in an expression tree, it can insert nodes that already exist in the right-hand-sides of the rules, but it can’t create new nodes. The result consists of the nodes that were already in the source expression and the nodes of the right-hand-sides of the applied rules. If we know that the transformation result must contain, for instance, the function StartsWith(), predicate >= over integers, a certain sub-query, or a getter of a property, then these elements must already exist somewhere in the source expression, or, more likely, in the rhs of a rule. Thus, independently of how simple or intelligent our rules might be, we need some kind of stock (or pool) of rules that contain all the needed “building blocks”. This matches good typical scenarios in commercial applications: the user can choose that or this existing filter and enter parameters, but can’t “invent” new filters, new sorting criteria, etc.
All rules in the stock are known at compile time and are checked by the compiler. This is a great advantage. If a property name or type changes, the compiler will find all the rules that you have forgotten to trim.
If it is not possible or not reasonable to hard code rules for all “building blocks” (moderate laziness is not a sin), additional rules can be created dynamically based on generic patterns. The rules are themselves (pairs of) expressions and hence the generic patterns can be rewritten to produce specific rules. The pattern gives the general structure of the needed expression and only individual nodes (more precise: only simple lambda expressions with one node and variables in their bodies) must be created calling constructor-like static methods of the Expression class. This approach is less secure and is applicable only to expressions that follow some generic pattern.
Final Remarks
This article is aimed to present the basics of rewriting query expressions. The classes in the library are surely not perfect, but they do the work. They can be made more intelligent to cover more cases. For instance, different patterns for Where conditions and OrderBy selectors can be used, if they make sense in an application. To illustrate the technique, I simply took some “classical” cases.
Modifying a GroupBy section should not be technically complex also.
And, of course, I will try to answer any questions.
