Introduction
In this "episode" of our G.A. tutorial, we shall go a little in-depth on the first stage of most G.A. problem solving steps. Like the rest of the tutorials,
we shall be applying the lesson learned in solving the Travelling Salesman problem. Since I would be using the Shark library, the solution used for both this and the rest
of the tutorial shall be the same as that originally proposed by the Shark library (as seen in their tutorial).
Background
This tutorial references the previous one. As such, I would sincerely advice you to first read up the previous one.
You can find it here.
Encoding Camelot
In the previous tutorial, we discussed the canonical view of genetic algorithms. We solved a funny example using the concept of evolution, a kick-ass technique
used by the family of evolutionary algorithms. For the rest of the tutorial in the series, we shall be looking deeper in to each step of our outline described earlier.
The first part of our outline is the community, and since I am in love with movies and animations, I titled it Camelot (you know the King Arthur thing? cool ).
Our community, Camelot, is made up of people (wow, really observable!). These individuals, like Arthur, have distinguishable characteristics. The physical appearance
such as height, skin color, foot size, etcetera are known as the phenotype. At the very root, our genes hold the representation of our phenotype (physical characteristics/appearance).
I like to see humans as a very huge and complex computer program (Machines). Our skin color, hair color, and body form are determined by some series of instructions
in our genes. See the genes as functions (methods in OOP). Obeying a basic principle of functions/methods, modularity, a gene holds just the instruction for a particular purpose.
These genes (methods) are then associated and bundled up into a DNA (Class). This DNA is further packaged into a chromosome (namespace :D). For the basics on G.A.,
we shall focus on chromosomes and genes.
For a slim tall blond lady, we could deceive ourselves that the instructions for these are in one chromosome and represent it like this:
Chromosome 1:
| Gene_Body_Size | Tall |
| Gene_Hair_Type | Blond |
| Gene_Sex | Female |
More foolishness:
Chromosome 1:
| Gene_Body_Size | 10001010101010111111001010101100101 |
| Gene_Hair_Type | 111111111111111111111111111111110011111101 |
| Gene_Sex | 10 |
Another word you just might come across in other tutorials is allele. An allele is an alternative form of a gene. In the table above, I represented
Female Sex Gene as “10”, I would probably, and foolishly of course, represent male as “01” and hermaphrodites as “11” or ‘’00”. These alternative forms
of the gene are called alleles. Tamam? (That’s “OK” in Turkish by the way).
More on alleles and chromosomes, say the same lady has blue eyes, pointed nose, broad shoulders, and sexy voice! We could once again deceive ourselves that
the instructions for these are in another chromosome and represent it like this:
Chromosome 2:
| Gene_Shoulder_type | Broad |
| Gene_Eye_Color | Blue |
| Gene_Nose_Type | Pointed |
| Gene_Voice | Sexy |
If these characteristics are our only concern, we can therefore model our imaginary individual with two chromosomes, chromosome1 and chromosome2, having 3 and 4 genes, respectively.
Okay, how is this biological concept related to genetic algorithms? In our award winning story in the first tutorial, we represented males and females as strings of bits.
In other words, we created a genotype for them. G.A. involves recombination and mutation of genes. Meaning there is a need to represent the entities
in the problem domain (people in the community) in their genetic form (genes/chromosomes). The process of coding these “genetic forms” is called encoding.
As “up” has “down”, “previous” has “next”, so does encoding has decoding. Decoding is the reconversion of a genotype to a phenotypic representation (bla bla bla).
There are no general rules for encoding; it is in fact problem specific.
Various encoding schemes exist. Binary encoding, like our example above, is the representation of the problem domain in binary form.
We also saw this in our award winning story in the previous tutorial where we represented male as:
int male[SIZE] = {1,0,1,0,1,0,1,0,1};
Binary encoding is actually the commonest and most primitive form of encoding in genetic algorithms.
Permutation Encoding
Permutation as we know deals with ordering. It is best used when the problem domain has to do with ordering – sequences, patterns, etc. For example:
Chromosome 1: 1R 8P 6S 3T 9U 2G
Chromosome 2: 5 3 8 3 2 7 5 9
*Click here for more on encoding schemes.
The House of Books
Don’t get excited guys, it’s just a phrase I use for a “library”. The G.A. communities have created G.A. libraries containing classes and methods for common G.A. operations
such as encoding, selection, mutation, recombination, archiving, etcetera. For the entire tutorial, we shall be using a component of the Shark library
called EALib (Evolutionary Algorithm Library). You can find it and its documentation here.
The Traveling Salesman Problem
A salesman, Johnny Walker, is supposed to visit 10 cities in Camelot. Each travelling connection is associated with a cost (i.e., the time for the trip).
The problem is to find the cheapest round-route that visits each city exactly once and returns to the starting point.
The figure shows the example used in this tutorial.
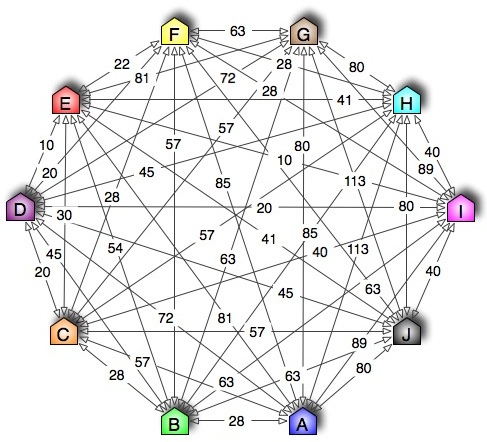
The first obvious puzzle is how to encode this. How do we represent this figure in a form suitable for programming?
| A
| B
| C
| D
| E
| F
| G
| H
| I
| J
|
A
| 0
| 28
| 57
| 72
| 81
| 85
| 80
| 113
| 89
| 80
|
B
| 28
| 0
| 28
| 45
| 54
| 57
| 63
| 85
| 63
| 63
|
C
| 57
| 28
| 0
| 20
| 30
| 28
| 57
| 57
| 40
| 57
|
D
| 72
| 45
| 20
| 0
| 10
| 20
| 72
| 45
| 20
| 45
|
E
| 81
| 54
| 30
| 10
| 0
| 22
| 81
| 14
| 10
| 41
|
F
| 85
| 57
| 28
| 20
| 22
| 0
| 63
| 28
| 28
| 63
|
G
| 80
| 63
| 57
| 72
| 81
| 63
| 0
| 80
| 89
| 113
|
H
| 113
| 85
| 57
| 45
| 41
| 28
| 80
| 0
| 40
| 80
|
I
| 89
| 63
| 40
| 20
| 10
| 28
| 89
| 40
| 0
| 40
|
J
| 80
| 63
| 57
| 45
| 41
| 63
| 113
| 80
| 40
| 0
|
You might be genius enough to try binary encoding, but I’ll lazy up and go with the Shark library guys and use an integer array.
const int cities[10][10] =
{
{ 0, 28, 57, 72, 81, 85, 80, 113, 89, 80 },
{ 28, 0, 28, 45, 54, 57, 63, 85, 63, 63 },
{ 57, 28, 0, 20, 30, 28, 57, 57, 40, 57 },
{ 72, 45, 20, 0, 10, 20, 72, 45, 20, 45 },
{ 81, 54, 30, 10, 0, 22, 81, 41, 10, 41 },
{ 85, 57, 28, 20, 22, 0, 63, 28, 28, 63 },
{ 80, 63, 57, 72, 81, 63, 0, 80, 89, 113 },
{ 113, 85, 57, 45, 41, 28, 80, 0, 40, 80 },
{ 89, 63, 40, 20, 10, 28, 89, 40, 0, 40 },
{ 80, 63, 57, 45, 41, 63, 113, 80, 40, 0 }
};
In our previous tutorial, we basically showed the concept of evolutionary strategy. We used one male and one female. Classical G.A. on the other hand deals with more
than one individual of the same kind; it deals with a population. This population creates the initial search space to exploit/explore using the concept of evolution.
There are no rules of thumb on the number of individuals (population size), though many G.A. peeps are somewhat in love with a population size of 200.
So let's represent Johnny's journey (cities) as having 200 parents and 200 offsprings.
PopulationT< unsigned int > parents ( 200, ChromosomeT< unsigned int >( cities ) );
PopulationT< unsigned int > offsprings( 200, ChromosomeT< unsigned int >( cities ) );
*Please see the documentation of the library for the syntax. It's well explained there, trust me!
Okay, we've seen encoding, learnt some biology, and why G.A. needs it. We've started a mission to help Johnny Walker walk through 10 cities in Camelot.
In the next tutorial, we shall be looking at the next concept in our outline (in the previous tutorial - problem in the community?) which has to do with "fitness".
