Introduction
This article discusses a processor benchmark utility. The results are surprising. Just as everything else (these days) breaks our preconceptions, so do processors.
Just the other day, I received an email about 21st century's broken preconceptions. It went something like this " .... the tallest basketball player is Chinese ... the most popular rapper is white, and the best golf player is ....". So there is little or no surprise to see a processor benchmark that shatters preconceptions.
Background
I was always curious about how the new generation processors measure up. How fast are they? Not just a number that represents the processor as a whole, but a real value that represents an honest measure of how many operations of a given kind the processor can do in a given time. For instance, how many integer additions a second. How many double divides a second? ....
Using the Code
The code is developed to use macros as the instrument of simplification. This way, the macro parameter can signify any desired benchmarking operation. The macro TIMEDOP (timed operation) is called with two parameters:
- The name of the function to generate
- The code to execute in the timing loop
TIMEDOP(do_int, count2++);
TIMEDOP(do_mul, count *= 33); TIMEDOP(do_div, count /= 13); TIMEDOP(do_sub, count -= 10);
TIMEDOP(do_mod, count %= 13);
TIMEDOP(do_str, memcpy(str, str2, 1024));
TIMEDOP(do_str2, memcpy(str, str2, 1));
TIMEDOP(do_dbladd, dop2 += dop1; dop1+=3);
TIMEDOP(do_dbladd3, dop2 = dop1 + dop3; dop1+= 2);
TIMEDOP(do_dbldiv, dop2 /= 103);
TIMEDOP(do_dblsin, dop2 = sin(dop1); );
TIMEDOP(do_func, noop(count2));
TIMEDOP(do_cos, cos(dop1););
TIMEDOP(do_tan, tan(dop1););
TIMEDOP(do_sqrt, sqrt(dop1););
int count = do_int();
QueryPerformanceCounter(&PerformanceCount);\
double dd = largeuint2double(PerformanceCount);\
QueryPerformanceCounter(&PerformanceCount3);\
double skew = largeuint2double(PerformanceCount3) - dd;\
... in the while loop ...
timeforonesec += skew;
if(currentcount - startcount > timeforonesec)
break;
Accuracy of the Measurement
Naturally, there are a lot of processes that compete for the processor. Thus, the benchmark measured flutters quite a bit. To compensate for that, the utility keeps a running average.
To test the accuracy of the code, and to prove if the compensatory trick works as intended, I was in a bit of a dilemma. The old Heisenberg principle kicked in, I could not observe the processor speed, as the observer process interfered with the findings. In other words, anything I tried to do with the processor interfered with the measurement.
Finally, in an idea to test the compensation code, I executed the benchmarking code snippet (from a macro) one hundred times in one test, and fifty times in the other test. If the compensating code works correctly, the results of the second test should be twice as large as the first test. It worked! Hurray!
I thought about the fact that measuring the processor speed involved a theory developed in connection with quantum mechanics. Very COOL. Isn't this what programming is all about?
Benchmark Items Described
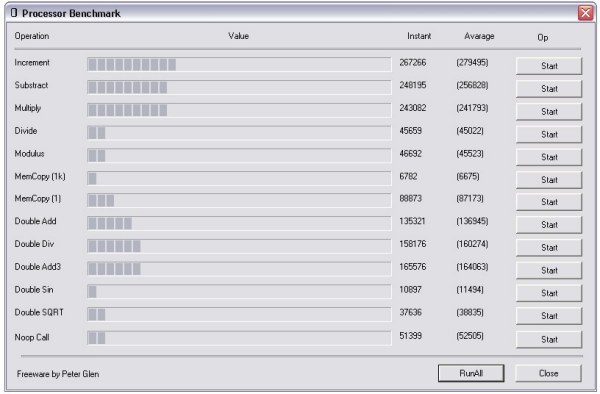
The following is a short synopsis of the items on the benchmark screen:
| Function Name | Code | Description | Notes |
do_int, | count2++ | Simple integer addition and/or increment | Increment and add at the same speed |
do_mul, | count *= 33 | Simple integer multiplication | Almost as fast as the add |
do_div | count /= 13 |
| Slower than double add |
do_mod | count %= 13 | Simple integer modulus | Same speed as div |
do_str | memcpy(str, str2, 1024) | Copy a 1k string | Involves memory. Nice test to see if the DDR 400 upgrade worked. |
do_str2 | memcpy(str, str2, 1) | Copy a 1 byte string | Library call overhead |
do_dbladd | dop2 += dop1; dop1+=3 | add two doubles | the optimizer knew bout the second var not changing., so we padded it. |
do_dbladd3 | dop2 = dop1 + dop3; dop1+= 2 | add two doubles, assign | padded as well |
do_dbldiv | dop2 /= 103 | double divide | faster than integer op |
do_dblsin | dop2 = sin(dop1) | trigonometric | slower than expected |
do_func | noop(count2) | call a blank function | debug build a lot slower |
do_cos | cos(dop1) | trigonometric | all trig functions execute with similar speed |
do_tan | tan(dop1) | trigonometric | |
do_sqrt | sqrt(dop1) | square root | the processor works hard here |
The Debug Build
The debug build has similar performance as the release build. The only significant difference is in the function calls. This is (possibly) due to the overhead of the debugger keeping tabs on the function call stack.
The Release Build
We had to disable optimization, as it breaks the code (naturally). The optimizer knows that we are making repeated calculations and repeated calls for no reason, so it optimizes it out.
Points of Interest
I have examined several processors with this utility (Core2, Sempron, AMD_64). To my surprise, I have found most of the adages learned in the past are broken. For example, when learning C or C++, one finds the recommendation that: 'variable++' is faster than 'variable += 1'. According to the benchmarks, var1 += var2 is the same speed as var1++;.
Another common knowledge is that working with doubles is slower than integers. Not according to the results of the benchmark. On my Athlon 64, the int divide is 45000/sec and the double divide is 153000/sec.
The integer multiply is just as fast as adding. Another unexpected result.
If all this sounds unbelievable, by all means, test it for yourself. Try the code, and if the code is in err, I would like to hear about it.
Feedback
Send me your processor's screen shot (peterglen@verizon.net).
History
- 29th May, 2008: Initial version
