Introduction
There are myriads of signals to analyse with spectral analysis methods: medical (HRV, ECG, EEG, EMG), geological, musical, etc... Among different analysis methods, there is a group of complexity metrics aimed to estimate how complex the signal is. Consider sine wave and random noise. Obviously the sine wave is a simple form of signal while noisy more complex. There are approximate (ApEn) and sample (SmEn) entropies metrics which provide such quantitative estimation of degree of complexity of the signal. ApEn and SmEn are better suited for complexity estimation of short-term noisy signals. They have the advantage that they analyse the original signal, as some complexity metrics need the original signal to be quantized to considerably small alphabet. So they are widely used in medicine for HRV data analysis. For EEG data analysis, they are applicable for estimation of some complex neuronal activity.
Background
You should read my article on the application of ApEn and SmEn for analysis of HRV data for prediction of paroxismal atrial fibrillation. There, more detailed explanation is presented. Here are just the formulas for ApEn and SmEn.
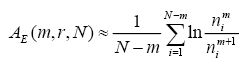
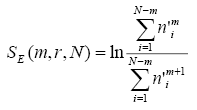
Using the Code
The ApEn code is shown below:
double ApEn(const double* data, unsigned int m, double r, unsigned int N, double std)
{
int Cm = 0, Cm1 = 0;
double err = 0.0, sum = 0.0;
err = std * r;
for (unsigned int i = 0; i < N - (m + 1) + 1; i++) {
Cm = Cm1 = 0;
for (unsigned int j = 0; j < N - (m + 1) + 1; j++) {
bool eq = true;
for (unsigned int k = 0; k < m; k++) {
if (abs(data[i+k] - data[j+k]) > err) {
eq = false;
break;
}
}
if (eq) Cm++;
int k = m;
if (eq && abs(data[i+k] - data[j+k]) <= err)
Cm1++;
}
if (Cm > 0 && Cm1 > 0)
sum += log((double)Cm / (double)Cm1);
}
return sum / (double)(N - m);
}
The SmEn code is shown next:
double SmEn(const double* data, unsigned int m, double r, unsigned int N, double std)
{
int Cm = 0, Cm1 = 0;
double err = 0.0, sum = 0.0;
err = std * r;
for (unsigned int i = 0; i < N - (m + 1) + 1; i++) {
for (unsigned int j = i + 1; j < N - (m + 1) + 1; j++) {
bool eq = true;
for (unsigned int k = 0; k < m; k++) {
if (abs(data[i+k] - data[j+k]) > err) {
eq = false;
break;
}
}
if (eq) Cm++;
int k = m;
if (eq && abs(data[i+k] - data[j+k]) <= err)
Cm1++;
}
}
if (Cm > 0 && Cm1 > 0)
return log((double)Cm / (double)Cm1);
else
return 0.0;
}
N is the size of signal pointed by data, std is dispersion of the signal, r is typically used as 0.2. SmEn and ApEn measure the ratio of how many similar patterns (within error r * std) there are for length m to length m+1.
History
- 17th June, 2008: Initial post
