Introduction
Artificial immune algorithms are inspired by the principles and processes of biological immune systems. This article shows how to develop a simple C# immune algorithm which models clonal selection, affinity maturation, and antibody interaction.
Background
Our immune system protects us from pathogenic organisms including bacteria, viruses, and toxins. It provides a number of levels of defence, with the skin being the first barrier to infection. Once pathogens have entered the body, they are handled with the innate immune system, and then by the acquired immune response system (see Fig 1.). The innate immune system provides protection that is always present. It uses roaming scavenger cells (phagocytes) to ingest abnormal cells, thus clearing the system.

Fig 1. Levels of defence in the immune system.
The acquired immune system provides protection that arises from an immune response. Substances capable of starting a specific immune response are called antigens. Nearly all pathogens are antigens. Antibodies are used by the immune system to identify and neutralise antigens (foreign bodies), and are produced from a kind of white blood cell called a B-cell.
Clonal selection models the production of antibodies which bind to specific antigens. The binding process of receptors is often likened to a key-lock mechanism. The probability of forming a bond (i.e., match strength) is referred to as affinity. Clonal selection establishes the idea that only those antibodies that recognise the antigens are selected for cloning and mutation. Cloned antibodies mutate in inverse proportion to how well they match the antigen so that better matching antigens are mutated less and weakly matching antibodies are mutated much more. This process is called affinity maturation, and improves the likelihood of antibodies forming a bond. Immune models also have to take into account the activity resulting from interactions between antibodies.
Optimisation by Immune Algorithm
From a computer science perspective, modeling the behaviour of the acquired immune system can provide potential new ways of solving problems. The function optimisation problem involves finding the best solution (either the peak or trough) to a function bounded by constraints.
In the example code, a test function has been used and is plotted in Fig. 2. This test function uses the sine function to produce the hilly plot, and so finding the highest peak is a challenge. The equation is given by:
Fitness = (15*x*y*(1-x)*(1-y)*sin(9*pi*x)*sin(9*pi*y))<sup>2</sup>
This is the function used by Barry Lapthorn in his article entitled “A simple C# genetic algorithm” located on the CodeProject website. The optimal solution for this problem is 0.879 at x=0.5 and y=0.5, which is the highest peak at the centre of the plot. Coincidently, the plot has been produced using SciLab, which is a free numerical computation package.
How can a clonal selection model be used to solve this optimisation problem? Well, if we consider an antibody as a potential solution (i.e., a cell object which has an x-y value) and the fitness function as the antigen, then the degree of fit or binding represents the quality of the solution. If we start with an initial population of antibody solutions and test them against the fitness function (antigen), then those with the highest affinity (i.e., best fit) are allowed to clone and mutate in the hope of finding a better solution.

Fig. 2. The test function (the highest peak solution is found at x=0.5 and y=0.5).
Consequently, an immune algorithm can be devised as follows:
- Generate an initial population of antibodies.
- Perform clonal selection to generate high affinity clones and mutate.
- Remove antibodies whose affinity with the antigen is less than a predefined threshold.
- Calculate affinity interactions between all antibodies in the system.
- Remove antibodies whose affinity with other antibodies is below a predefined threshold.
- Introduce randomly generated antibodies into population (diversity).
- Repeat steps 2 to 6 until the stopping criteria is met.
Algorithm
The code contains four essential classes. These are:
- The main form class which provides a simple GUI
- The immune algorithm controller class
- The antibody class
- The fitness function class
The code has been commented and so should be straightforward to follow. I have used code snippets found on AISWeb (see link below) to develop the clonal selection operators. Particularly helpful was the code example contributed by Paul Andrews.
The fitness function class has a static method called evaluateFunction() which returns the fitness value given x and y input values. The antibody class attempts to model a biological antibody cell. It has methods for cloning itself, finding the affinity with another antibody and an affinity based mutation. Each antibody represents a candidate solution, which in this example is simply an x-y value. The immune algorithm controller class allows parameters to be defined, and has a method called GoOptimise() which creates an initial population of antibodies and iterates a solution until the stopping criteria (a maximum number of generations) is reached.
Using the Code
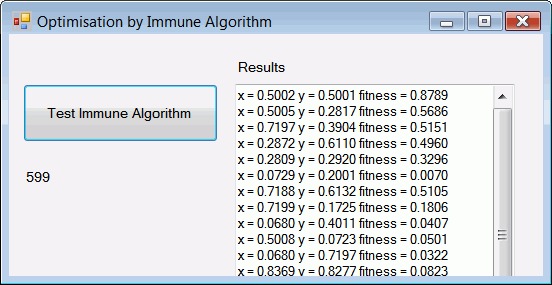
The antibodies (candidate solutions to the function optimisation problem) that are generated by the immune algorithm are displayed in a text box. The best antibody is displayed first, and should be a good match to the required solution for this problem which, as stated above, is 0.879 at x=0.5 and y=0.5. An immune algorithm is a non-deterministic algorithm, meaning that it gives different results on different runs.
There is plenty of scope for experimenting with parameter settings, which are currently set as below in the immune algorithm controller class. It is necessary to set threshold values for removing (suppressing) antibodies from the population pool (clonalSelectionThreshold, removeThreshold). The settings used for these threshold values were derived by a process of trial and error. The parameter called antibodyNumber determines the initial number of antibodies used to solve the problem or, in biological terms, neutralise the antigen. This has been set to 50. The cloneNumber parameter sets the number of clones generated during clonal selection. Affinity based mutation is set using the mutationFactor parameter. Constraints for the x and y values are imposed using the lowerBoundary and upperBoundary parameters.
antibodyNumber = 50; cloneNumber = 20; maxGens = 600; mutationFactor = 80; removeThreshold = 0.2; clonalSelectionThreshold = 0.01; diversity = 0.5; lowerBoundary = 0.0; upperBoundary = 1.0;
Points of Interest
The code was written using SharpDevelop2.2, but can also be compiled using Microsoft Visual Studio Express. Some initial coding difficulties relating to object cloning and a compile error which occurred when using a random seed derived from System.DateTime.Now.Ticks were encountered. Object cloning was solved by using the ICloneable interface which requires that a Clone() method is written.
Summary
There are many articles on the web which provide more information regarding immune algorithms than covered in this introduction. Some links are given below, but Googling the term “artificial immune system” will yield many more. The article has illustrated some of the main concepts of immune algorithms including clonal selection, affinity maturation, and antibody interaction.
There is potential for further investigation. It would be interesting to look into the discrimination between antibodies destined to be deleted and those not, and new types of operators for cloning and mutation. If you wish to explore immune algorithms further, I suggest your next step is to visit the AISWeb using the link below.
Links
History
- July 2008 - First release
