Introduction
std::map is a one of the most useful containers in the standard template library (STL). It allows the implementation of sorted dictionaries. It is usually implemented using a red-black tree data-structure which guarantees a good (O(log n)) performance, and is the container-of-choice for most tasks (unless you are using a new Standard Library implementation - e.g., Visual Studio 2008 with Feature Pack 1 or GCC 4.2 - in which case, you can use the new TR1 unordered_map and unordered_set).
Although std::map and std::set are good enough for most tasks, the red-black tree implementation is no speed-demon. The provided code implements a "drop-in" replacement for std::map and std::set (we haven't implemented the multi- variants), which benchmarks show is two times faster.
Note that the implementation imposes restrictions on the Key type for the map: a special "infinity" value is required.
Boost and a modern C++ compiler are required.
Using the Code
smap and sset are drop-in replacements for std::map and std::set, respectively. Here is an example of using smap:
#include <iostream>
#include "sti/smap"
using namespace sti;
int main()
{
typedef smap<char, int> Map;
Map my_map;
my_map.insert(std::make_pair('a', 1));
my_map.insert(std::make_pair('A', 1));
my_map.insert(std::make_pair('b', 2));
my_map.insert(std::make_pair('B', 2));
Map::const_iterator it = my_map.find('a');
std::cout << "my_map[" << it->first << "]= " << it->second << std::endl;
my_map['a'] = 10;
for (it = my_map.begin(); it != my_map.end(); ++it)
{
std::cout << "my_map[" << it->first << "]= "
<< it->second << std::endl;
}
my_map.erase('a');
it = my_map.find('b');
my_map.erase(it);
std::cout << "Items: " << my_map.size() << std::endl;
return 0;
}
Similarly, for sset:
#include <iostream>
#include "sti/sset.h"
using namespace sti;
int main()
{
typedef sset<int> Set;
Set my_set;
my_set.insert(1);
my_set.insert(10);
if (my_set.find(1) != my_set.end())
std::cout << "Found 1 in set" << std::endl;
else
std::cout << "Couldn't find 1 in set" << std::endl;
return 0;
}
sset and smap are defined in sset.h and smap.h respectively, and defined as follows:
namespace sti
{
template<
class Key,
class Type,
class Traits = std::less<key>,
class Allocator = std::allocator<std::pair <const Key, Type> >,
int BN = 48,
class key_policy = default_stree_key_policy<Key>,
class value_policy = default_smap_value_policy<Key, Type>,
class gist_traits = default_gist_traits<Key>
> class smap;
template<
class Key,
class Traits = std::less<Key>,
class Allocator = std::allocator<Key>,
int BN = 48,
</key>class key_policy = default_stree_key_policy<Key>,
class gist_traits = default_gist_traits<Key>
<key /> > class sset;
}</key>
Template parameters
Choosing BN
Except for the last (BN) template parameter, this definition is identical to std::map and std::set. BN is similar to the "order" of a B-Tree - it defines how many elements should be kept in a single node. Playing with this value can have significant impact on performance. BN values of 32 to 128 seem to perform well (see Implementation below for more details).
key_policy
key_policy controls how keys are stored in internal nodes (see implementation below). key_policy can be either std::tr1::true_type or std::tr1::false_type. If key_policy is true_typememmove(). Otherwise, only pointers to keys are stored in the node itself, along with a "gist" (size_t) value which is calculated from the key (using gist_traits).
By default, for small, simple types (POD types - int, char, etc.), key_policy is true_type, while for other types, it is false_type.
We don't want to store more complex types as part of the node, since moving them (for split/merge operations) will be expensive (and wrong, as we then must call the copy constructor).
It is therefore recommended to use the default key_policy, and in any case, do not use true_type for types that require a non-trivial copy constructor.
gist_traits
The gist_traits parameter is only valid when key_policy is true_type.
When key_policy is true_type, we only keep pointers to the keys in the inner nodes. Comparing these pointers will cost us in performance (see below - Memory as a Bottleneck). Keep a "cheap" value in the node itself that can be used to compare values quickly (comparing two integral values is virtually "free").
Here's a code that explains the idea:
struct KeyWrapper
{
KeyType* _key;
size_t _gist;
};
bool less(KeyWrapper l, KeyWrapper r)
{
if (l._gist < r._gist)
return true;
else if (l._gist > r._gist)
return false;
else
retrurn less(l->_key, r->_key);
}
If gist<sub>1</sub> is the gist of key<sub>1</sub>, and gist2 is the gist of key<sub>2</sub>, then the following must hold:
- if
key<sub>1</sub> < key<sub>2</sub>, then gist<sub>1</sub> <= gist <sub>2</sub> - If
key<sub>1</sub> == key<sub>2</sub>, then gist<sub>1</sub> == gist<sub>2</sub> - if
key<sub>1</sub> > key<sub>2</sub>, then gist<sub>1</sub> >= gist<sub>2</sub>
A default gist_traits is provided that simply returns 0 for all keys.
For strings, a specialization is provided that implements the following (sizeof(char)==1 for simplicity):
struct string_gist
{
const static size_t chars_per_size_t = sizeof(size_t);
size_t operator()(const std::string& s) const
{
sz = std::min(sz, chars_per_size_t);
size_t r = 0;
for (size_t i = 0; i < sz; ++i)
r = (r<<8) + (size_t)c[i];
return r;
}
};
value_policy
The value_policy parameter controls how an item is stored in the map. If value_policy is false_type, then each item inserted into the map is allocated separately, and a reference to the item is guaranteed to be valid (unless the item is erase()d, of course). If value_policy is true_type on the other hand, the items are stored as part of the stree nodes - and therefore can be reallocated when these nodes are split or merged.
By default, value_policy is true_type if both key and value are simple, small types, and false_type otherwise.
Performance
A simple benchmark is provided with the source. The benchmark creates a large container, then erase(), find(), and insert() are called repeatedly with random values. The same benchmark is performed for a std::map<int, int> and smap<int, int>.
Here are the results when compiling with Visual Studio 2008 with standard "Release" optimizations (Core 2 6400, 2GB memory running on WinXP):
STL map time: 1548678032
smap time: 740111472
smap therefore shows x2.09 performance improvement vs. std::map.
Caveat
To simplify implementation, all iterators are invalidated if the container is modified, so the following code which (should) work with std::map will throw an exception:
smap<int, int> m;
smap<int, int>::iteraor it;
for (it = m.begin(); it != m.end(); ++it)
{
if (it->second == 1)
erase(++it); }
As a workaround, erase(iterator) returns an iterator to the next element after the element deleted, so we can write instead (this will also work with Visual Studio's STL implementation which extends erase() in the same way):
smap<int, int> m;
smap<int, int>::iteraor it;
for (it = m.begin(); it != m.end(); ++it)
{
if (it->second == 1)
it = erase(it);
In addition, there is a limitation on the Key type: a special infinite() value is required which must be larger than any key.
Implementation
Memory as bottleneck
The basic idea of stree is that in modern architectures, memory has become the main performance bottleneck: accessing a random main-memory location requires tens (and in some cases, hundreds) of clock cycles. New memory architectures mainly improve the transfer rate: once you get to a memory location, reading 1 or 100 bytes takes about the same time. Cache memory reduces memory-access latency by storing a low-latency copy of frequently used memory - accessing random (or wide-spread) memory locations will result in cache misses.
Disk-based data structures face the same issues - e.g., caching; high cost of accessing the first bit vs. accessing the next one, etc. The solution - using "flatter" trees (B-Trees) and keeping multiple items together, is now appropriate for memory-based data structures.
A bit on skip lists
A skip-list is basically a sorted linked-list with "shortcuts" which allow a fast (O(n) on average) find operation.
To construct a skip-list, start with a sorted linked list (let's call this the 0-level list). Now, choose (randomly) half of the nodes and connect them by another linked-list (the 1-level list). Now, choose randomly half the nodes in the 1-level list and create a 2-level list, and so-on until no elements are chosen for some level.
To search a linked-list, start by progressing along the highest-level list, "dropping" to the next level, if progressing to the next node will get us past the desired element. On average, no more than 3 elements need to be examined in each level.
The 1-2-3 Top-Down skip-lists
Munro, Papadakis, and Sedgewick have proposed an alternative version of the skip-list which is deterministic. In addition, they described a simpler implementation of the skip-list - the 1-2-3 Top-Down skip-list.
Here is an example of a 1-2-3 skip list:
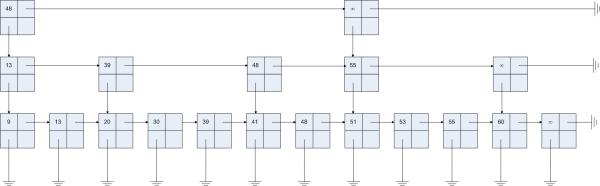
This structure is similar to a binary tree with the node leafs connected in a linked-list. Search starts with the head node at the top left (48), and goes right as long as the searched key is greater than the node's key, in which case, we drop to the next level and continue our search. Similar to a B+ Tree, items are stored only in the leafs.
Unlike a skip-list, this is a deterministic data structure: the "gap" between two nodes is always between 2 and 3. For example, there is a 3-node gap between the head node (48) and the node to its right. That gap includes the nodes 13, 30, and 48 at the middle level. Similarly, there is a 2-node gap between nodes 13 and 30 at the middle level, which includes the nodes 9 and 13 at the bottom. Whenever the gap goes outside the allowed range (2-3), the structure is fixed by adding (or removing) nodes.
stree
The 1-2-3 skip list allows only gaps of size of at most 3. However, there is nothing to prevent us from allowing larger gaps. This will somewhat reduce the memory requirements (less inner nodes), but will increase the search time (need to check more items per level).
Another possible modification would be to store all nodes of a single gap in an array, which we call an stree. Here is the stree version of the same skip-list:

By allowing larger gaps (up to BN) and replacing the link-list of items in a gap by an array, we get a data-structure quite similar to a B+ Tree.
History
- July 15, 2008: Published.
- July 17, 2008: Added more details on the implementation.
memmove() only used for simple types. - Aug 06, 2008: Removed the need for
infinite(). Supports all key and data types. Template parameters control whether to allow "movement" of value_type.
