Introduction
I wanted to know how a regular expression parser works. So I did some Googling and found some cool articles that describe the process of how regular expressions find a match. I listed the articles in the reference section of this article. I have implemented this parser based on my research. I will not go too much into describing the process and the theory behind the regular expression, since the articles in the reference section cover this very well (the topic of regular expressions is huge and will require a book to explain thoroughly).
In this article, I will simply show an implementation of a simple Regular Expression parser (or Mini Regular Expression Parser). I will go on using the terms Automata, NFA, DFA, Minimum DFA, state, transitions, and epsilon transition. If you do not understand these terms, I highly recommend you read up on some of the articles in the reference section before continuing.
So you ask, "why this one?" This implementation is done step-by-step, so it makes it easy for someone wanting to learn how regular expressions work. Other features:
- Has a GUI that helps you understand the states and transitions
- Use of ^ and $ tokens to specify match at the beginning and ending of the pattern respectively
- A C# implementation, quite object-oriented
- Easy to understand code with comments
- Has a feature allowing you to control the greediness of the parser - allowing you to experience the different behavior of greediness.
- Not limited to ASCII characters (0-255)
- This implementation is more complete than most parsers I came across.
So I wanted to share the implementation with CodeProject users. BTW: This is my first submission to CodeProject, hope you like it.
Features
The table below shows the symbols the parser supports.
| Symbol | Description | Example |
| ? | (Quantifier) Match the precedent character zero or one time | "A?" finds zero or one A |
| + | (Quantifier) Match the precedent character one or more time | "A+" finds one or more As |
| * | (Quantifier) Match the precedent character zero or more time | "A*" finds zero or more As |
| _ (underscore) | Any single character. | "a_b" will find "abb", "aab", "acb" and will not find "ab" |
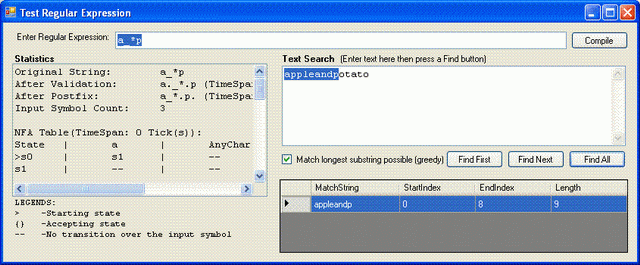
| _* | Match any character zero or more time (wildcard). | "a_*p" will find "appleandp" in string "appleandpotato". |
| [ ] | Any single character within the specified range ([a-f]) or set ([abcdef]). | "[C-P]arsen' finds "Carsen", "Larsen", "Karsen", and so on. |
| [^] | Any single character not within the specified range ([^a-f]) or set ([^abcdef]). | "de[^l]-*' finds string beginning with "de" and where the following letter is not l. |
| $ | Token to specify to match at the beginning of the string | "AA$" finds last two As in "AAA" |
| ^ | Token to specify to match at the end of the string | "^AA" finds first two As in "AAA" |
| \ (escape) | You can escape the following characters:
\(, \), \n (new line), \r (carriage return), \[, \], \*, \?, \+, \t (tab)
| "\n\n" finds any two consecutive occurrence of new line.
"a]b[cd\]]" is a valid pattern.
|
Some parsers use a dot(.) to denote any single character, instead of _(underscore). If you want, you can change this in the source code by simply changing the value of the constant that is defined for this.
You can control the greediness of the parser by setting the RegEx.UseGreedy property. If you set this property to false and use the pattern "a_*p" in string "appleandpotato" — it will match "ap" and not "appleandp".
The parser validates the input pattern string for its correctness. If it encounters an error in the syntax, it will report error with details information (i.e., error position, length, and type of error) accurately.
Using the Code
The algorithm in this parser follows the lecture notes of Mr. Mike Clark. Unfortunately, he had taken the notes offline since I downloaded them. So I am making them available here.
I find these notes rather simple and very easy to understand. And I structured my code according to the steps mentioned in these notes. If sometimes you find it difficult to understand what my code is doing (I hope you won't), please read one of these relevant notes.
This parser is written in C# using Visual Studio 2005. Below is the partial class diagram with the key classes of the component.

The Set class is a simple representation of a Set in mathematics. Since .NET does not come with a Set class, I had to write one. The Map class is a map between a key and one or more objects, also not in .NET. The State class holds the data structure of the automata. RegEx is the main class that actually uses other classes. The RegExValidator class is used to validate a pattern string. Validation is done using Recursive Descent Parsing. Besides validating the pattern, it does two other tasks: insertion of implicit tokens making it explicit and expanding character classes. i.e.,
- "AB" -> "A.B" (inserting the concatenating operator(.) )
- "A.B" -> "A\.B" (inserting the escape)
- "[A-C]" -> "(A|B|C)" (expanding the range)
- "(AB" -> Reports error with mismatch parenthesis
You will find a description of methods of the classes in the source code as comments.
The sequence diagram below shows how to use the parser.

The code snippet below shows how you can use the RegEx class:
private void TestMatch()
{
RegEx re = new RegEx();
string sPattern = "a_*p";
ErrorCode errCode = re.Compile(sPattern);
if (errCode != ErrorCode.ERR_SUCCESS)
{
string sErrSubstring = sPattern.Substring(re.GetLastErrorPosition(),
re.GetLastErrorLength());
string sFormat =
"Error occured during compilation.\nCode: {0}\nAt: {1}\nSubstring: {2}";
sFormat = String.Format(sFormat, errCode.ToString(),
m_regEx.GetLastErrorPosition(), sErrSubstring);
MessageBox.Show(sFormat);
return;
}
int nFoundStart = -1;
int nFoundEnd = -1;
string sToSearch = "appleandpotato";
bool bFound = m_regEx.FindMatch(sToSearch, 0, sToSearch.Length - 1,
ref nFoundStart, ref nFoundEnd);
if (bFound)
{
int nMatchLength = nFoundEnd - nFoundStart + 1;
if (nMatchLength == 0)
{
MessageBox.Show("Matched an empty string at position " +
nFoundStart.ToString() + ".");
}
else
{
string sMatchString = sToSearch.Substring(nFoundStart, nMatchLength);
MessageBox.Show("Match found at: " + nFoundStart.ToString() + "\n" +
sMatchString);
}
}
else
{
MessageBox.Show("No match found.");
}
}
Points of Interest
The NFA models for quantifiers *, + , and ? can be found in the articles I mentioned.
When I was implementing the parser, I had a lot of trouble with a couple of transitions:
_ (underscore) -any single character
[^A] -Complement of character set
I did not find information regarding these transitions during my Googling.
After much trial and error, I came up with the NFA models that work fine. Using these models, you do not have to modify the original algorithm at all.

This "AnyChar" transition is handled in the RegEx.FindMatch method as an special case. If the current state does NOT have a transition over the current input symbol, it checks to see if the current state has a transition over the "AnyChar" symbol. If so, it uses the transition.

The complement of character set uses an "AnyChar" transition and a "Dummy" transition. If the current state uses a transition that is forbidden (i.e., A in [^A] ), it ends up in a state that has only one transition going away from it — that is the "Dummy" transition and that state is not an accepting state. A "Dummy" transition is NEVER used in the actual process and thus the parser reaches a dead-end state, effectively resulting in a mismatch. If the current state does not have any transition over the current input symbol, it uses the "AnyChar" transition and ends up in accepting state effectively matching the correct sub/string.
Also, the RegEx.FindMatch method requires some discussion as well. Without the implementation of ^(match at start), $(match at end), _(any single character), _*(wildcard - any number of any character), and greediness (control of it) features, this method would be much simple like below.
public bool FindMatch(string sSearchIn,
int nSearchStartAt,
int nSearchEndAt,
ref int nFoundBeginAt,
ref int nFoundEndAt)
{
if (m_stateStartDfaM == null)
{
return false;
}
if (nSearchStartAt < 0)
{
return false;
}
State stateStart = m_stateStartDfaM;
nFoundBeginAt = -1;
nFoundEndAt = -1;
bool bAccepted = false;
State toState = null;
State stateCurr = stateStart;
while (nSearchStartAt <= nSearchEndAt)
{
char chInputSymbol = sSearchIn[nSearchStartAt];
toState = stateCurr.GetSingleTransition(chInputSymbol.ToString());
if (toState == null)
{
toState = stateCurr.GetSingleTransition(MetaSymbol.ANY_ONE_CHAR_TRANS);
}
if (toState != null)
{
if (nFoundBeginAt == -1)
{
nFoundBeginAt = nSearchStartAt;
}
if (toState.AcceptingState)
{
bAccepted = true;
nFoundEndAt = nSearchStartAt;
}
stateCurr = toState;
nSearchStartAt++;
}
else
{
if (!bAccepted)
{
nSearchStartAt = (
nFoundBeginAt != -1 ? nFoundBeginAt + 1 : nSearchStartAt + 1);
nFoundBeginAt = -1;
nFoundEndAt = -1;
stateCurr = stateStart;
}
else
{
break;
}
}
}
return bAccepted;
}
But with those features added, this method gets a little more logic oriented. The current implementation looks like this:
public bool FindMatch(string sSearchIn,
int nSearchStartAt,
int nSearchEndAt,
ref int nFoundBeginAt,
ref int nFoundEndAt)
{
if (m_stateStartDfaM == null)
{
return false;
}
if (nSearchStartAt < 0)
{
return false;
}
State stateStart = m_stateStartDfaM;
nFoundBeginAt = -1;
nFoundEndAt = -1;
bool bAccepted = false;
State toState = null;
State stateCurr = stateStart;
int nIndex = nSearchStartAt;
int nSearchUpTo = nSearchEndAt;
while (nIndex <= nSearchUpTo)
{
if (m_bGreedy && IsWildCard(stateCurr) == true)
{
if (nFoundBeginAt == -1)
{
nFoundBeginAt = nIndex;
}
ProcessWildCard(stateCurr, sSearchIn, ref nIndex, nSearchUpTo);
}
char chInputSymbol = sSearchIn[nIndex];
toState = stateCurr.GetSingleTransition(chInputSymbol.ToString());
if (toState == null)
{
toState = stateCurr.GetSingleTransition(MetaSymbol.ANY_ONE_CHAR_TRANS);
}
if (toState != null)
{
if (nFoundBeginAt == -1)
{
nFoundBeginAt = nIndex;
}
if (toState.AcceptingState)
{
if (m_bMatchAtEnd && nIndex != nSearchUpTo)
{
}
else
{
bAccepted = true;
nFoundEndAt = nIndex;
if (m_bGreedy == false)
{
break;
}
}
}
stateCurr = toState;
nIndex++;
}
else
{
if (!m_bMatchAtStart && !bAccepted )
{
nIndex = (nFoundBeginAt != -1 ? nFoundBeginAt + 1 : nIndex + 1);
nFoundBeginAt = -1;
nFoundEndAt = -1;
stateCurr = stateStart;
}
else
{
break;
}
}
}
if (!bAccepted)
{
if (stateStart.AcceptingState == false)
{
return false;
}
else
{
nFoundBeginAt = nSearchStartAt;
nFoundEndAt = nFoundBeginAt - 1;
return true;
}
}
return true;
}
Initially I fought myself trying not to add any additional logic in the FindMatch method and was trying to find solutions for those features using the NFA model. That effort took me nowhere and I ended up adding a little addition to the logics in this method. But now all these features work very well.
Final Word
This is a simple implementation. More features can be added to this demo code if you want. If you add more features to this demo code presented here, I would very much like to have a copy of that code if it is OK with you. You can use the code anyway you like under the CodeProject license (CPOL). I don't think it would be too difficult to port this demo code to C++ if you want.
History
- August 1, 2008 -- Initial submission
- February 24, 2009 -- Xawiersas found an error in the code (see below) So I fixed it and restructured the code to make it more readable
- June 24, 2009 -- Updated source and demo project
References
