Introduction
Although data is obviously stored in memory or on disk in binary form, .NET automatically converts it into base 10 (decimal) whenever we want to see the data or set values. It does have a little functionality for getting or setting values in other bases, as listed below.
Inbuilt functions
Setting an Int32 (base = 2 for binary, 8 for octal, or 16 for hexadecimal): Convert.ToInt32 (string, base). E.g.:
string binaryString = "11111111";
int i = Convert.ToInt32 (binaryString, 2);
i now equals 255.
Alternative for hexadecimal only:
int i = 0xFF;
i now equals 255.
Getting a value from an Int32: Convert.ToString (integer, base). E.g.:
int i = 255;
string binaryString = Convert.ToString (i, 2);
binaryString now equals 1111111.
This class library
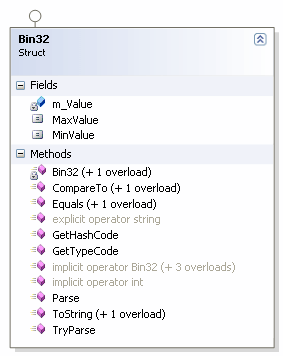
These suffice in most situations, but I’ve often found I need a more natural/flexible way that basically wraps these functions up. This class library is a few simple bits of code to address this. All the structs are built around an Int32 (m_Value), so are therefore called Bin32, Oct32, and Hex32.
The first thing you’ll notice in each struct are several implicit and one explicit operator methods.
In Bin32, the first one is:
public static implicit operator Bin32(int value) {... }
This bit of magic allows us to accept an int directly to create an instance of Bin32, without needing to call an overloaded constructor in our code (it's done automatically to a private constructor). You can do this, for example:
Bin32 binaryValue = 255;
instead of the usual:
Bin32 binaryValue = new Bin32(255);
The next is similar, but allows us to use a string:
public static implicit operator Bin32(string value) {... }
So, we can simply use:
Bin32 binaryValue = "11111111";
A little further down is a similar method to the first, but with Bin32 and int reversed.
public static implicit operator int(Bin32 value) {... }
This allows us to automatically use our value as an int without explicitly casting.
Bin32 binaryValue = "11111111";
int i = binaryValue;
The next line is different in that it is explicit rather than implicit:
public static explicit operator string(Bin32 value) {... }
By using the explicit keyword, it means we have to explicitly cast to this type to use the method.
Bin32 binaryValue = "11111111";
string binaryString = (string)binaryValue;
Why not use implicit here? Well, having multiple implicit return types can cause some major headaches. Just try changing the explicit to implicit, and then try:
Console.WriteLine(binaryValue);
Oops! There is a lot of ambiguity created as it doesn’t know what to write to the console – more than one choice is too many!
Initially, I had the string as implicit and the int as explicit. It can work fine that way, but a lot more code is needed as all unary, binary, logical, and conditional operators then require overloading. Keeping the int as implicit, we get to use the code that Microsoft has already done for the Int32 operators :-).
For more information on operator overloading, see my article: An Introduction to Operator Overloading in C#'.
As well as the explicit cast there are also the two ToString methods (one for Oct32).
I’ve implemented the standard IComparable and IEquatable interfaces. The Parse, ToString, and TryParse methods are mainly covered in by the in-built functions I covered at the beginning of the article.
There is one other class here – a static class called ExtensionMethods, where a few simple extension methods are declared to give added functionality to ints and strings without having to actually call any Bin32, Oct32, or Hex32 instances ourselves.
In use
Add a reference to BinOctHex.dll to your project. Using these structs is very easy. A simple example is attached. All the usual stuff you can do with an int can be done with any of these (including bit shifting, which makes more sense in hex and binary). You can also do operations on combinations of these. E.g.:
(bin number % hexnumber) / octnumber;
Motivation for use
I often need to do calculations on multiple binary and hexadecimal numbers and have the results displayed in either base (octal less frequently, but I included it for completeness).
Imagine something simple such as:
((1 + 2 + 3 + 4 + 5) % 4) * 15 = ?
Easy if they're all ints, but what if they're mixed binary and hex strings?
((00000001 + 00000010 + 00000011 + 00000100 + 00000101) % 00000100) * 0F = ?(base 8)
Currently, you'd have to convert each string manually to an int, and then convert again to display the answer in the correct base. Using this, you just perform the calculation as it looks.
string a1 = "00000001";
string b1 = "00000010";
string c1 = "00000011";
string d1 = "00000100";
string e1 = "00000101";
string f1 = "00000100";
string g1 = "0F";
int h1 = (
(Convert.ToInt32(a1, 2) +
Convert.ToInt32(b1, 2) +
Convert.ToInt32(c1, 2) +
Convert.ToInt32(d1, 2) +
Convert.ToInt32(e1, 2))
% Convert.ToInt32(f1, 2))
* Convert.ToInt32(g1, 16);
Console.WriteLine(Convert.ToString(h1, 8));
Bin32 a2 = a1;
Bin32 b2 = b1;
Bin32 c2 = c1;
Bin32 d2 = d1;
Bin32 e2 = e1;
Bin32 f2 = f1;
Hex32 g2 = g1;
Oct32 h2 = ((a2 + b2 + c2 + d2 + e2) % f2) * g2;
Console.WriteLine((String)h2);
I also timed the code above, and both performed in roughly the same time - sometimes the first section was fractionally quicker, sometimes the second - so it's not slowing anything down at all. Working with straight ints is about 50x faster, but if you have data in a different base, then you have to do the conversion anyway. If you want to change it to an int to remove the overhead - that's what the implicit casting is for.
History
