Summary
Depending on the complexity of the grammar, a hand-built recursive descent compiler may actually be the best option. It can be quicker to implement than learning a compiler-compiler system, plus it avoids having to integrate the compiler-compiler's runtime into your source code base. But it also involves risks that must be carefully weighed.
Introduction
Many years ago, smart people recognized that building compilers was tough. BUT, they also recognized that there were many repeated patterns within the code for compilers. And where there is the combination of smart people, AND patterns, software magically evolves*. Thus was born "compiler-compilers" to assist in converting grammar specifications into compilers without the tedium of writing the same code over and over for those patterns. Famous among these compiler-compilers is YACC -- Yet Another Compiler Compiler.
This article demonstrates a few of the patterns of compilers, and how to go about implementing a simple compiler WITHOUT a compiler-compiler. To help make the ideas concrete, we work through the task of building an expression evaluator.
This is NOT a tutorial on compiler theory or on language design. There are several textbooks on that subject. Plus there's always that repository of all useful knowledge, Wikipedia if you want that. Rather, this article is a pragmatic look at the patterns that go into building a simple recursive descent compiler. If you want, you can download the full source code for the expression evaluator.
But first, some important preliminaries: Before reading this article thinking that you're going to implement a compiler, follow this flowchart:
Do you need to implement a fairly simple parser/compiler?
- no
{ save a link to this article, and come back when you need it.
If you're anything like me, you won't remember enough of the
details to make it worth reading anyway. Heck, I wrote it,
and I don't even remember what's in here!
}
- yes
{ Can you afford to hire someone who really understands
compilers?
- yes
{ just do it! Save yourself a lot of pain.
}
- no
{ Do you have enough time to learn to use a good
compiler-compiler?
- yes
{ this is probably the smart move. Good compiler-
compilers reduce the risk of missing things, or of
accidentally coming up with a compiler that accepts
constructs you hadn't planned on, which are
probably meaningless anyway.
}
- no
{ I feel sorry for you. Be sure you implement an
exhaustive test suite.
}
}
}
Several years back, I needed to implement a very small compiler for reading and processing industry-standard stacking sequence codes for lamina layup in composite structural materials (like fiberglass or carbon-fiber composites) into strength and stiffness results for the final product. Because the grammar was quite small, I opted to not dig out my compiler-compiler (a commercial product called "LALR" written by Paul B. Mann, one of the geniuses of our day) and decided instead to implement a simple top-down recursive descent parser. It took me a few hours of focused thought to get it working correctly.
One of the advantages of NOT using a compiler-compiler is that you don't have to drag in all the (possibly licensed) parsing engine and lexing engine code. Another advantage, as I alluded to earlier, is that it MIGHT actually be quicker than learning (or re-learning) the compiler-compiler's system. All compiler-compilers that I'm aware of have their own syntax for inputs, then requirements for where to put output files, how to build the resulting generated code, etc. Once you learn all that, it's pretty quick to make changes and re-generate. But there IS DEFINITELY a learning curve.
Even if you do use a compiler-compiler, you still have to implement the action code associated with each individual grammar production. That means you STILL have to REALLY UNDERSTAND what you're trying to accomplish. The compiler-compiler really only helps you implement the parser. The actions you take as the parser dissects the input are still up to you. You still have to build the backend data structures, the logic, the compiler's output, etc.
The risks of rolling your own compiler (instead of using a compiler-compiler) is that you are building the code for each production from scratch, and you can miss little things that will cause your parser to misbehave, or to behave differently on similar productions on which it SHOULD behave pretty much the same.
Well, having said all that, let's throw caution to the wind and get started.
Getting Started: The Project Requirements
In my expression evaluator project, I needed to read in a mathematical expression from an appropriate .ini file, and then to evaluate the result of that expression at run-time, with parameter values that could only be known at run-time. The expression was to be evaluated tens of thousands of times so it needed to be compiled only once into an intermediate-form that would be very fast to evaluate. I also wanted it to be able to deal with differences in the formula for different points in the domain; just like a real mathematical function would:
f(x) = {0 when x<0, x when 0 <= x <= 2, 4-x when x>2}
Thus, my goal was to implement an expression evaluator that:
- Accepts replaceable parameters
- Accepts logical constructs
- Executes branching based on logical results
- Produces a pre-compiled version for speedy execution
The simple approach for my application would have been to drag in a scripting language that could handle all of these with ease. If you have the environment available to you, using PERL, or VBScript would probably take care of all the details for you (actually, I don't know whether they pre-compile an expression, or whether they recompile the expression each time it's evaluated). Unfortunately, in my environment, I had no pre-made scripting language that would be available, so I needed to implement the expression evaluation code myself.
The three primary tasks here are:
- Come up with the intermediate-form. This is quite independent of writing the compiler. The compiler will simply put the human-written expression INTO that intermediate-form. Part of this task is also to implement the evaluator function that turns the compiled expression plus replaceable parameters into a final single number.
- Come up with an appropriate grammar. This part is critical, and determines the precedence and associativity of the operators. If this part is wrong, nothing else is going to work as expected. I'll share with you some of the joys I had in getting certain aspects of the grammar incorrect, and having to work thru them.
- Implement a compiler that both recognizes and parses the grammar correctly, AND takes appropriate construction actions (constructing that intermediate-form from part 1) along the way.
--Task 1: Design the Intermediate Form --
The intermediate-form I settled on is very similar to RPN (Reverse Polish notation: see http://www.hpmuseum.org/rpn.htm), a stack based representation of an expression formally called "postfix" form. Humans write expressions in "infix" form where the operators are in-between the operands. As such, we frequently have to add parenthesis to indicate precedence. Postfix expressions don't need parenthesis because they just perform all operations in left to right order. Here are a couple of examples.
infix form : 7 + 2
postfix form: 7 2 +
infix form : 5*sqrt( 4 + 3*4 )
postfix form: 3 4 * 4 + sqrt 5 *
To evaluate a postfix expression, a pointer into the postfix expression represents the "top of the stack". As the expression is traversed from left to right, when operators are encountered, the appropriate number of operands to the left of the operator is processed and the results replace the operator.
Stepping through that last example expression, stopping when operators are recognized and executed, the expression evolves as follows:
3 4 * 4 + sqrt 5 *
^
3 4 12 4 + sqrt 5 *
^
3 4 12 4 16 sqrt 5 *
^
3 4 12 2 16 4 5 *
^
3 4 12 2 16 4 5 20
^
When finished, the final answer is on the top of the stack (last position of the postfix expression).
The problem with using this exact process is that I needed to be able to repeat the process many times. You can see that the postfix expression is consumed along the way, making it unavailable for re-use. Also, so far there is no provision for replaceable parameters. And lastly, the expression evaluator must recognize that '+', '*', and "sqrt" are operators, not operands. That likely involves decision making at run time, which, for speed sake I wanted to avoid or to make as simple as possible. All of these obstacles could probably be overcome using a strict postfix idiom, but I chose a slightly different approach.
After stewing about it for a while, I settled on a hybrid approach that involved four arrays: one array of constants that is populated at compile time, one array of instructions that is also populated at compile time, one array of parameters that is passed to the evaluator routine for use at evaluation time, and a scratch-pad array -- the stack, used at evaluation time. The structure looks something like this:
typedef struct ExpressionStruct {
double *constants;
int constantsLen;
int *instructions;
int instructionsLen;
} Expression_T;
For the following input, "6 * sqrt( 5 + 3*4 )", the generated arrays are:
constants: 3 4 5 6
instructions: PUSH_C PUSH_C MUL PUSH_C ADD SQRT PUSH_C MUL
Where PUSH_C means "get the next constant from the constants array and push it onto the local stack". There is also a PUSH_P "Push Parameter" instruction. See the algorithm below.
The evaluation routine runs through the entire instructions array, and depending on the instruction either copies the next constant to the scratch-pad stack, copies one of the parameters to the same stack, or executes the indicated instruction (like SQRT or ADD or MULT) using values near the top of the stack. It looks like this:
double evaluate( Expression_T* ep, double* parameters )
{
int constantIndex = 0; int ndx; double stack[50]; int stktop = -1;
for( ndx=0; ndx < ep->instructionLen; ndx++ )
{
int instruction = ep->instructions[ndx];
if( 0 == instruction )
stack[++stktop] = ep->constants[constantIndex++] ;
else if( instruction < 0 )
stack[++stktop] = parameters[-instruction-1];
else switch( instruction )
{
case ADD: stktop-- ;
stack[stktop] += stack[stktop+1];
break;
case MUL: stktop-- ;
stack[stktop] *= stack[stktop+1];
break;
case SQRT: stack[stktop] = sqrt( stack[stktop] );
break;
default: error("Unrecognized operator");
}
}
return stack[0]; }
The actual code is quite a bit longer owing to a much longer switch statement (more operators). Plus it includes lots of debugging and tracing code. It can be downloaded from links elsewhere in this post.
Note that in the example code in this article, there are some hard limits embedded within the code; like the "double stack[50]" above. This is especially bad form unless you plan to test the stack height at every PUSH, and throw a runtime error if something goes wrong. If you use the code where you expose the functions to the outside world, like if you're getting the infix expression from a web-form or some such thing, using hard limits exposes you to nasty runtime things like buffer overruns. For example, the expression...
"1*(1*(1*(1*(1*(...)))))"
...will eventually overflow the 50 element stack if continued long enough. The actual code uses dynamic memory for the stack as well as for the instructions and constants arrays. While I won't discuss it in the article, the actual stack usage can be computed at compile time, and the correct amount of stack pre-allocated so that run-time stack-overflow tests won't even be necessary. Again, you can see how this is done in the actual code within the addInstruction() function.
That finishes the task of designing the intermediate form that the compiler will generate.
--Task 2: Design the Expression Grammar --
We're going to be recognizing human-readable infix expressions. Later in task 3, we'll implement the production actions associated with each grammar rule, converting them to the quasi-postfix format discussed above. For now, we just need to write the BNF that describes the grammar.
The first thing to note is that we want the compiling process to end when it hits the end-of-string marker (the null terminator). Before then, it better have recognized an "expression". Thus, we can say:
goal:
-> expression '\0'
where "expression" is one of the non-terminals we're going to implement.
I'm going to attempt to express the expression grammar from the "bottom-up". That is, thinking about the lowest, most primitive forms, and then building upon them.
It seemed to me that the most primitive operands within the grammar would be literal numbers, and parameters. That is, everything that ends up on either side of an operator must ultimately come down to something that can be reduced to just a number. To indicate the most basic of operands, I use the non-terminal name t0. As we progress to more complicated forms, we'll march through t1, t2, t3, etc.
t0:
-> number
-> parameter
It also occurs to me that among the most basic forms, we should include anything within parenthesis. Thus, we should add:
-> '(' expression ')'
where we've yet to define what an expression is, but it will end-up being just what you think it is; a series of operands and operators that reduce to express a single number.
We should also count function calls as most basic. Thus, we should add:
-> funcname '(' list ')'
where a list will be a comma separated list of expressions.
And one last thing: if we want to allow named constants, like "pi", we should do it here. I only implemented "pi", but more could be added if desired.
Thus, the complete description of the t0 non-terminal is:
t0:
-> number
-> parameter
-> '(' expression ')'
-> funcname '(' list ')'
-> named_constant //I'm actually only allowing pi for simplicity.
I'll go ahead and note here that on my first pass, I thought the branching construct should go here. Thus, I had another production rule like this:
-> expression '?' expression ':' expression
where you'll recognize the use of the C language "conditional". More about this later. Here I just want to point out that this was a mistake, and caused the parser to act in very odd ways, looking for and processing tokens in a way that I had not intended at all. After looking to the C language specification to see how THEY implemented it, I realized it needed to be at the LOWEST precedence, not the highest. Thus, I moved it out of the definition for t0.
Having decided what our "primitives" are, we begin progressively adding complexity to our terms by following the old PEMDAS pattern: Parenthesis, Exponentiation, Multiplication, Division, Addition, Subtraction (or as my kids learned it, "Parachute Expert My Dear Aunt Sally"). We've already taken care of parenthesis, so we can begin progressively creating non-terminals for each precedence level of operator, paying close attention to the operator's associativity.
Actually, the PEMDAS pattern is not completely correct as we should apply unary negation ahead of exponentiation. I want to be able to say -2^3 and have it mean (-2)^3, not -(2^3). In this example, you get the same answer, but what about in a formula that uses a parameter instead of a literal: for example, -p1 ^ 3.2 where you know ahead of time that the parameter value p1 is negative, and its sign must be changed BEFORE attempting to exponentiate it with a fractional exponent. Obviously the binding should be (-p1)^3.2.
t1: //unary prefix operators.
-> t0
-> '-' t0
-> '+' t0
The purist in me says we ought to be able to negate (or posate?) ANY single term, and thus we should rewrite it with a recursive definition as follows:
t1:
-> t0
-> '-' t1
-> '+' t1
making this a right recursive rule (because the non-terminal symbol "t1" shows-up on the right end of (at least) one production rule). But the pragmatist in me says, "how many times should we really allow...
x + - - - - + + + - - 5
...anyway?" Thus, I'm overruling the purist, and sticking to my decision to ONLY allow a single negation (or posation, er uh, positivation, or maybe positively_plusillyation) operator, and leaving it as originally written.
NOW that unary operators are handled, let's do exponentiation:
t2:
-> t1
-> t1 '^' t2
Note the right recursion. This guarantees that the ^ operator will bind from right to left. That is, in a sequence of operations like 4 ^ 3 ^ 2, the compiler will recognize that "4" must remain as a t1, and "3 ^ 2" must be reduced to a t2. In reducing "3 ^ 2" to a t2, it must leave "3" as a t1, but reduce "2" to a t2. Thus, the implied binding will be from right to left, effecting 4^(3^(2)).
Next is multiplication and division. They are at the same level of precedence, and thus all go within the same non-terminal, and are evaluated in first-come first-served (left to right) order. We're going to add another operator to the classic PEMDAS, and implement modulo as well.
t3:
-> t2
-> t3 '*' t2
-> t3 '/' t2
-> t3 '%' t2
Note the left recursion. Again, this is what forces left associativity of the operators. We'll find that most of our operators are actually left associative.
And finally addition and subtraction: Again, we want them to associate left to right, so we need left recursion.
t4:
-> t3
-> t4 '+' t3
-> t4 '-' t3
That finishes the simple calculator part of formula evaluation. However, as stated earlier, I want the ability to do tests and branching to different formulas based on those tests. Thus, the first thing we need to implement is logical comparisons: less than, greater than, equals, etc. Turns out that the precedence of logical equals needs to be lower than the comparison operators, so we need to do the less than and greater than first.
t5:
-> t4
-> t5 "<" t4
-> t5 "<=" t4
-> t5 ">" t4
-> t5 ">=" t4
t6:
-> t5
-> "not" t5
By placing "not" at one precedence level lower than the comparison operators,
not x < 7
evaluates as not(x < 7), instead of (not x) < 7. I believe this makes more intuitive sense than having the "not" bind with x first.
Note that by putting it at this level of precedence, "not x" cannot be used in contexts that require a t5, a t4, a t3, a t2, a t1, or a t0. That is, you can't say "6 * not p2" to effect a 0 or 6 toggle based on p2. You CAN however effect exactly this by simply enclosing the "not p2" in parens. "6 * (not p2)" DOES effect a 0 or 6 toggle. Because of the parenthesis, "(not p2)" is a primitive (i.e. a t0) and can be used in any context, whereas "not p2" is a t6 and is limited in where it can be used.
Note also that we're patterning this after the unary negation (t1). Thus we only test t5s on the right hand side. As with unary negation, it is NOT recursively defined.
t7:
-> t6
-> t7 "eq" t6
-> t7 "not_eq" t6
One might wonder why not to include equality tests as higher precedence than "not" so that...
not y eq x
...evaluates as not(y eq x) instead of how it's actually going to evaluate: (not y) eq x.
The answer is that there is a separate operator for not-equal, and to compute not equal, we should just use that operator. Again, if "not y eq x" bound as not(y eq x), how would we effect (not y) eq x? We would be forced to use parens.
I'll note here that I was well into the testing aspect of the project when it finally dawned on me (via a test) that the "eq" token created a slight conflict. Consider this construct:
6.5eq7.0
Obviously this is false, but it illustrates the problem. Because I'm using strtod() to pick up numbers, the strtod() function scans up through 6.5e thinking it's getting a scientific notation number, like 6.5e3 for 6500. Then it sees the 'q' and aborts. Yes, I could have fixed this by writing my own number scanning function. But this seemed like overkill. Instead, I just added the C operators "==" and "!=" to the t7 rule so someone can write "6.5==7.0" and get the result they want (of course they could also have just added spaces: "6.5 eq 7.0" works just fine). Besides, when the "6.5eq" fails it throws an error and does not quietly march forward and produce erroneous results. I deemed that "good enough"!
t7:
-> t6
-> t7 "eq" t6
-> t7 "==" t6
-> t7 "not_eq" t6
-> t7 "!=" t6
For logical completeness, here are the ands and ors.
t8:
-> t7
-> t8 "and" t7
t9:
-> t8
-> t9 "or" t8
Both are left recursive meaning they associate left to right. Since "and" is higher precedence than "or",
x and y or z and w
evaluates as (x and y) or (z and w)
We're only lacking two things now: "expression"s, and "list"s for use with function parameters. First, the left associative list:
list:
-> expression
-> list ',' expression
Note that, unless we allow null expressions, this way of defining a list is not going to permit empty lists. In our grammar, that is not a problem since we’re not going to be calling functions with empty parameter lists anyway. But in a more general grammar where we wanted to allow empty parameter lists, we would need to consider implementing empty expressions (and consider how to deal with the complexity that will produce) or add another production to permit empty lists:
list:
-> expression
-> list ',' expression
-> ''
But now we’ve introduced some interesting issues. First, input like the following is now legal:
somefunc( , , 2)
Unless you know what you want to do with such input, that is, what kind of structures you want the compiler to build in response to such input, they are meaningless anyway and you don’t want to allow them.
Next, you’ve just introduced a conflict into the grammar. Consider how such a grammar should parse a simple function call: sin( 2 ). Realize that before the “2”, there is an empty string (of zero length). It’s invisible to us, but not to the parser. Should the parser first accept the zero-length string, reducing it to a “list”? Or should it first attempt to recognize and accept an expression? It is clear to US that the right answer is to look for an expression first, then if one is not found, to accept nothingness as a valid list. But to implement this, you’ll have to be careful of the order in which you do things.
Turns out, if all you want is to implement empty parameter lists (and not to accept constructs like somefunc( , , 2)), this is probably the wrong place to do it. You should probably modify the t0 non-terminal by adding the following rule:
-> funcname '(' ')'
We'll talk more about this when we implement the list non-terminal.
This finishes everything except the "choose which expression" operator. Since only the expression non-terminal is left to define, this is the place to incorporate the branching operator. I opted to use the C language ?: conditional operator for branching.
expression:
-> t9
-> expression '?' expression ':' expression
That finishes the grammar. Now on to task number 3: actually implementing it as a compiler.
--Task 3: Building the Compiler --
Parsers (input language recognizers) are broadly placed into one of two categories: Top-down, or bottom-up. In a bottom-up parser, a list of "next legal tokens" is generated for each "state" the parser finds itself in. If the next token read from the input doesn't match one of the items in the list, there's an error in the input. If it does match, the parser executes whatever action (that you design as part of making the "parser" into a "compiler") that is associated with that state and that token, and then moves to the next parser state associated with that state and that token. Bottom-up parsers may execute faster than top-down parsers, but they are difficult to build by hand.
Top-down parsers on the other hand can be built in a "recursive-descent" fashion almost directly from the grammar specification. Consider the t2 non-terminal,
t2:
-> t1
-> t1 '^' t2
we can implement this very simply with the following function. In this function, the parameter "ifp" is the infix expression pointer address. We need the address of the pointer so we can modify where the expression pointer is pointing to as we "consume" tokens from the input. As you'll see, all the non-terminal functions return a value that can be used to express success or failure: success when one of the production rules is recognized, and failure when none of the rules are recognized.
int t2( Expression_T* ep, const char** ifp )
{
if( not t1(ep, ifp) ) {
return 0; }
ltrim( ifp );
if( **ifp == '^' ) {
*ifp++ ; if( t2(ep, ifp) ) { addInstruction( ep, EXPON ); return 1; }
else
{
return 0;
}
}
return 1;
}
Pattern: Recursive descent parsers can be written almost directly from the grammar definition. You check for the existence of non-terminals in the input by simply calling the function that implements that non-terminal, then testing the return to see if it succeeded. You check for literals in the input by first bypassing white-space, then doing a direct '==' character comparison, or a strcmp(). As we match input literals (tokens), we "consume" them by advancing the input pointer past them.
Pattern: Anytime you have two rules that begin the same, make sure you don't prematurely accept the shorter rule (like t2 -> t1 in the above example) without checking if a longer rule is actually present (like t2 -> t1 '^' t2 in the above example). If a rule is seen, execute a construction action if required (like the “addInstruction()” action above). Indicate whether any of the rules were seen by returning a zero (for failure) or non-zero (for success).
Saving State
Note that in each case where we returned zero (failed to see a valid production), we just glibly returned, without restoring the input pointer (ifp) to where it had been before our failed t1 or t2 attempt, even though either of those actions could have advanced the pointer to who-knows where, and made it impossible to continue with an alternate action. For example, consider the following grammar:
tx:
-> first_production
-> next_production
-> last_production
first_production:
-> "hello world" ';'
next_production:
-> "hello world" '?'
We implement first_production like this:
int first_production( Expression_T* ep, const char** ifp )
{
ltrim( ifp ); if( 0 == strncmp( *ifp, "hello world", 11 ) and ( *ifp += 11, ltrim( ifp ), ';' == **ifp ) ) {
*ifp ++ ; return 1; {
else
return 0; }
Now suppose the actual input looks like this:
"hello world?"
Within first_production, the input is advanced past "hello world" and is pointing at the '?' when the production fails and returns. tx now attempts next_production, but since the input is pointing at the '?' instead of at "hello world?" it will also fail, even though it should succeed.
Clearly, if first_production fails, before trying next_production, we must restore the pointer to where it was at the beginning of the function. The same thing if next_production fails; before trying last_production, we must restore the input pointer (the state).
And while we're talking about it, note that state is actually much more than just the input position pointer. In our compiler, state also includes the instruction array end pointer, and the constants array end pointer. In a more complicated compiler, it might include other things as well.
The question is, WHERE should we restore state? That is, which function should be responsible for restoring state: the calling function, or the called function?
The way t2 is implemented, we are clearly ASSUMING that if a function in the call chain ahead of t2 needs the state restored, it will take care of it, because t2 certainly didn't do it!
This gets down to a design decision: should the caller, or the called function do state restoration. Well, consider the first few non-terminals and production rules of our grammar:
t1: -> t0
...
t2: -> t1
...
t3: -> t2
...
t4: -> t3
...
If we rely on the called function to restore state, we're going to have code that looks like this:
int t1( Expression_T* ep, const char** ifp )
{
State_T s;
save_state( &s, ep, ifp );
if( not t0( ep, ifp ) )
{
restore_state( &s, ep, ifp );
return 0;
}
else ...
}
int t2( Expression_T* ep, const char** ifp )
{
State_T s;
save_state( &s, ep, ifp );
if( not t1( ep, ifp ) )
{
restore_state( &s, ep, ifp );
return 0;
}
else ...
}
etc.
Each non-terminal function must save a local copy of the state before it does anything else. Thus, saving and restoring state becomes a rather time and stack consuming process as each non-terminal function drills into the next lower non-terminal function.
Now suppose we let the calling function take care of restoring state. Then the example functions above become:
int t1( Expression_T* ep, const char** ifp )
{
if( not t0( ep, ifp ) )
{
return 0;
}
else ...
}
int t2( Expression_T* ep, const char** ifp )
{
if( not t1( ep, ifp ) )
{
return 0;
}
else ...
}
Much simpler, much faster, and uses less stack space for local variables.
Pattern: Let the calling functions restore their own state if they need to. Any time there are alternate rules (that is, if failing the first rule doesn't doom the whole non-terminal), that non-terminal will need to save state before drilling down with other non-terminal calls.
As we will see, most of our grammar rules will be like the t2 rule implemented above, where, if the first production fails, there's no point in moving forward; that non-terminal has already failed. Since there was no alternative, there was no point in saving the state within that non-terminal.
Before moving forward with more code, lets update our Expression_T type to take care of that annoying double pointer input "**ifp".
typedef struct ExpressionStruct {
double *constants;
int constantsLen;
int *instructions;
int instructionsLen;
const char* infix;
} Expression_T;
This will allow us to pass just one argument to the non-terminal functions, and make manipulating the input pointer easier. When we initiate the compiling process, we'll set the infix member to the actual expression the user wants compiled.
Left Recursion Pattern
Now let's demonstrate more patterns by writing the functions for different non-terminals. The t2 rule demonstrated right recursion. Now let's demonstrate left recursion by implementing t4.
t4:
-> t3 //rule #1
-> t4 '+' t3 //rule #2
-> t4 '-' t3 //rule #3
Before we get started, note that the ONLY way to get a t4 (from a non-t4) is by seeing a t3. If we don't begin by seeing a t3, there is no way to move forward. Thus, while there ARE three separate rules, implying we should save state, the first one is mandatory, so there's really no point is saving state before it.
int t4( Expression_T* ep )
{
InstructionEnum_T ins;
if( not t3( ep ) )
{
return 0;
}
while(
ltrim( &(ep->infix) ),
(ins=ADD , '+' == *(ep->infix))
or (ins=SUBT, '-' == *(ep->infix)) )
{
ep->infix += 1; if( t3( ep ) ) {
addInstruction( ep, ins ); }
else
}
return 1; }
Pattern: Implement grammar left recursion via a "while" loop. Don't carelessly create an infinite loop by recursively calling a non-terminal that will bring you right back to the same position in the code!
More State Saving
So, what should we do about that 'else' clause after seeing "t4 OP ", but then NOT seeing a successful t3 non-terminal? I know of two possible approaches.
The Purist Approach
In the purist approach, we should attempt to isolate the t4 non-terminal logic from every other non-terminal, and make it stand alone. In this way, if any other parts of the grammar should ever change, the t4 is rock-solid, and will not need to change. Let's think about how to do this. Regardless of whether we want to be a purist, it's worth examining anyway because there may be other situations where this is the only choice we have.
Let's consider input that looks like this:
"4 + 5 - 6 * 7"
The first '4' is a t0 which ultimately reduces to a t3, which generates success for rule #1. We then move into the while loop looking for a '+' or a '-' sign. We get it at the '+' sign. We then call t3 to see what's on the right hand side of the '+' sign. The '5' reduces to a t3 and returns success, which signals we can again reduce via rule #2 to t4. We then continue the while loop and see the '-' sign. We call t3 again and now the entire "6 * 7" reduces to a t3. We move forward still within the while loop looking for the next '+' or '-' sign. There isn't one so the while loop exits and we return 1 (the last line of the function).
Now consider this input:
"4 + 5 - &x"
This isn't legal input for our expression grammar, BUT as stated earlier, perhaps the grammar will be extended in the future and we want our rule to stand alone and still work correctly. We need to somehow indicate that the "4 + 5" portion reduced successfully, but return failure for the "- &x" portion of the input. Suppose that we add a rule to the t1 non-terminal:
t1: //unary prefix operators.
-> t0
-> '-' t0
-> '+' t0
-> '&' t0 //new rule
In this case, since t1 is higher precedence than t4, the "&x" input will successfully reduce to a t3, and everything will work fine: NO ERROR.
But suppose instead that the t6 non-terminal gets a new rule:
t6:
-> t5
-> "not" t5
-> t6 '-' '&' t0 //new rule
Remember our input:
"4 + 5 - &x"
Within the t4 non-terminal, the "4 + 5" reduces to a t4, then the minus sign is consumed and the t3 fails with the "&x" input. If we could somehow indicate that the "4+5" successfully reduced to a t4, then it would in-turn reduce to a t5 (via t5 rule #1), which would reduce to a t6 (via t6 rule #1), and we'd be ready to move forward with the rule "t6 -> t6 '-' '&' t0" PROVIDED the minus sign that was consumed in the t4 was replaced.
That is, within the t4 non-terminal, within the while loop, we should keep track of the state at the LAST SUCCESS, and if we do encounter a failure, restore that state before returning SUCCESS.
Let's rewrite t4 with this new information (most of the comments removed to highlight our new-found policy):
int t4( Expression_T* ep )
{
InstructionEnum_T ins;
State_T s;
if( not t3( ep ) )
{
return 0;
}
while(
ltrim( &(ep->infix) ),
(ins=ADD , '+' == *(ep->infix))
or (ins=SUBT, '-' == *(ep->infix)) )
{
saveState( &s, ep ); ep->infix += 1; if( t3( ep ) ) { addInstruction( ep, ins );
}
else { restoreState( &s, ep );
break; }
}
return 1;
}
This represents a deviation from our earlier policy of not restoring state prior to returning to a calling function. But in this case, since we are inside of a loop, there's just no way for the calling function to know how far along we got before we quit seeing successful reductions.
Actually, since the while loop represents recursion (left recursion), once we get into the loop, THIS FUNCTION IS the calling function (as well as the called function). It is implicitly calling itself. Thus, when we restore state, t4 essentially IS the calling function restoring the context. So this actually is not a deviation from earlier policy.
Pattern: Within a while loop that represents left recursion, you should save state after each successful production, and if you advance state while looking for a pattern, but the pattern fails, restore state before returning the success indicator. Remember, if you saw ANY successful rules, you return "SUCCESS", not "FAILURE".
The Pragmatic Approach
I started the last section by saying there were TWO WAYS to deal with the else clause, and the way we just discussed was the "purist" approach. The other approach is to simply look around the grammar and see where else the '+' and '-' signs appear. Turns out they only appear in this t4 rule, and in the higher-precedence t1 rule. Unlike our fictitious example where we purposely installed a '-' sign in a lower-precedence rule, in the real grammar, once you get a "t4 '-' " there simply are NO OTHER LEGAL productions. If you DON'T get a t3, you have an error in the input. So for our real grammar, we can simplify t4 even more by just raising an error if we get a '+' or '-' but then DON'T get a t3.
int t4( Expression_T* ep )
{
InstructionEnum_T ins;
const char* oldfix;
if( not t3( ep ) )
{
return 0;
}
while(
ltrim( &(ep->infix) ),
(ins=ADD , '+' == *(ep->infix))
or (ins=SUBT, '-' == *(ep->infix)) )
{
ep->infix += 1; oldfix = ep->infix; if( t3( ep ) )
addInstruction( ep, ins );
else error( oldfix ); }
return 1;
}
We still sort-of saved state via the oldfix variable, just not as much state -- it's only a single pointer instead of stack-tops, etc. AND we saved it AFTER advancing past the '+' or '-' token. We needed this in order to get a decent error message if the t3 does fail. If we don't care about telling the user what went wrong, we could even skip this part. BUT, not giving some clue to the user about what went wrong is BAD FORM. Your users will hate you... They will curse you as they pull their hair out hunting for what went wrong. They will lay in bed at night and dream-up bad things to do to you -- ways to make you PAY!
SAVE YOURSELF! Just give them a decent error message for pity's sake.
As noted earlier, this version of t4 is no longer independent of the rest of the grammar. If other parts of the grammar change, t4 needs to be reexamined to see whether it is still correct to raise an error within this context.
Pattern: If you KNOW within a production that you've encountered an error in the input, you can just abort right there (with a nice error message of course), and not worry about returning up the call chain.
Greedy Input
Now let's implement the t5 non-terminal. As you'll see, it is pretty much exactly like t4, EXCEPT that there is a subtlety in how to match "<=" instead of "<", and ">=" instead of ">". Here we must be sure to use a greedy algorithm when attempting to consume the comparison token. If we don't, we can incorrectly match the shorter token.
t5:
-> t4
-> t5 "<" t4
-> t5 "<=" t4
-> t5 ">" t4
-> t5 ">=" t4
int t5( Expression_T* ep )
{
InstructionEnum_T ins;
const char* oldfix;
int toklen;
if( not t4( ep ) )
{
return 0;
}
while(
ltrim( &(ep->infix) ),
(ins=LT_EQ, toklen=2, 0 == strncmp( ep->infix, "<=", 2 )) or (ins=LT , toklen=1, 0 == strncmp( ep->infix, "<", 1 )) or (ins=GT_EQ, toklen=2, 0 == strncmp( ep->infix, ">=", 2 )) or (ins=GT , toklen=1, 0 == strncmp( ep->infix, ">", 1 ))) {
ep->infix += toklen; oldfix = ep->infix;
if( t4( ep ) ) addInstruction( ep, ins ); else
{
error( oldfix );
}
}
return 1; }
Primitives
The code for the t0 (primitives) non-terminal illustrates the requirement to store state between rules, and it illustrates a greedy algorithm in searching for function names.
But before we write it, we need a list of function names that we're going to allow. We'll binary-search this list when looking for a match within the input, so it must be in alphabetic order.
const char* funcnames[] =
{ "abs", "acos", "asin", "atan", "atan2", "ceil", "cos", "cosh", "erf"
, "erfc", "exp", "fact", "floor", "gamma", "ln", "lngamma", "log10"
, "mod", "pow", "sin", "sinh", "sqrt", "tan", "tanh"
};
int t0( Expression_T* ep )
{
double val;
char* end;
const char* oldfix;
int numargs; State_T s;
FindRet_T fr;
ltrim( &(ep->infix) );
oldfix = ep->infix ;
if( val = strtod( ep->infix, &end ), (ep->infix != end) ) {
addConstant( ep, val ); addInstruction( ep, PUSH_C ); ep->infix = end;
}
else if(('p' == *(ep->infix) or 'P' == *(ep->infix)) and isdigit( *(ep->infix + 1) ) and ( 0 == *(ep->infix + 2) or not isdigit( *(ep->infix + 2) ) or 0 == *(ep->infix + 3) or not isdigit( *(ep->infix + 3) )) ) {
int pnum = *(ep->infix + 1) - '0';
ep->infix += 2;
if( isdigit( *(ep->infix) ) ) {
pnum *= 10;
pnum += *(ep->infix) - '0' ; ep->infix += 1; }
if( 0 == pnum ) error( oldfix );
addInstruction( ep, (Operation_T)(-pnum) ); }
else if( 0 == strncmp(ep->infix, "pi", 2) )
{
addConstant( ep, 3.1415926535897932384626433832795 );
addInstruction( ep, PUSH_C ); ep->infix += 2; }
else if( saveState( &s, ep ) , ( ( '(' == *(ep->infix)) and (ep->infix++ , expression( ep )) and (ltrim( &(ep->infix) ), ')' == *(ep->infix)) )) {
ep->infix++; }
else if( restoreState( &s, ep ), fr = binarySearch(oldfix,funcnames,
FUNCNAMES_LENGTH,sizeof(char*),funcAryNameCompare) ,
( not fr.notfound and ( ep->infix += strlen(funcnames[fr.index]), ltrim( &(ep->infix) ), '(' == *(ep->infix) ) and (ep->infix++ , (numargs=list( ep ))) and (ltrim( &(ep->infix) ), ')' == *(ep->infix)) ) )
{
if( numargs-1 != opStkUse[fr.index] )
error( oldfix ); ep->infix++; addInstruction( ep, (Operation_T)(fr.index) ); }
else
{
return False; }
return True;
}
Pattern: When accepting one of the language tokens, always use greedy input. Look for and accept the longest legal token.
Note that the list() non-terminal function returned the number of items in the list (see the line containing “numargs=list( ep )”), NOT a Boolean value as every other non-terminal does. There’s no reason why you can’t return whatever information you need from any non-terminal function -- including a structure, if that makes sense. Here, we needed to verify that the number of parameters being passed to a function was the correct number. To do this, we encoded success and failure within the return value: zero for failure, and num_items+1 otherwise. That way, we can accept empty parameter lists but still get a “success” indicator. Remember, we talked earlier about other changes we would have to make to actually accept empty parameter lists. Here I just wanted to point out how we might want to deal with a "list" non-terminal if it did accept zero parameters.
Pattern: The return value from a non-terminal does not have to be Boolean – it can be whatever makes sense. You just have to be able to determine from the return value whether the non-terminal succeeded, or failed.
More Interesting Subtleties
The "list" non-terminal brought up some interesting points regarding empty lists that we should probably look at. Although not used within the expression evaluator being built for this project, it's worth looking at how "empty" rules might be dealt with.
Let's look at two different scenarios: The first is where we just want to accept empty parameter lists, and return the value "1", indicating success, but "1-1" (or zero) items actually in the list. Here's the code:
static int list( StaticExpression* ep )
{
const char* oldfix;
int ret = 1;
if( not expression(ep) ) { if( ep->infix = ltrim( ep->infix ),
')' == *(ep->infix) )
{
return 1; }
return 0; }
while( ep->infix = ltrim( ep->infix ),
',' == *(ep->infix) )
{ ret++ ;
ep->infix += 1; oldfix = ep->infix;
if( not expression(ep) ) error( oldfix );
}
return ret;
}
And here's another shot at it, but this time we actually accommodate the empty string production, which allows inputs like somefunc( , , 1.5, ). You'll have to decide what eval() action should happen for a null parameter.
static int list( StaticExpression* ep )
{
int ret = 1;
State_T s;
saveState(&s, ep);
if( not expression(ep) ) { restoreState(&s, ep);
addInstruction( ep, NULL_LIST_ELEMENT ); }
while( ep->infix = ltrim( ep->infix ),
',' == *(ep->infix) )
{ ret++ ;
ep->infix += 1; saveState(&s, ep);
if( not expression(ep) ) { restoreState(&s, ep);
addInstruction( ep, NULL_LIST_ELEMENT ); }
}
return ret;
}
The Branching Mechanism
The last thing I want to cover in depth in this article is the branching mechanism used to implement the ?: conditional operator. It is contained within the "expression" non-terminal.
The branching construct implemented here is effectively an if/else construct (as opposed to a simple "if" construct). As such, it needs two jumps: one conditional jump to the "do this if test is FALSE" section, and one unconditional jump to the "after the whole thing" section. The flow is like this:
if( test is false ) //these two lines form the
goto FALSE_SECTION; //conditional jump section.
//otherwise, just proceed.
<code for true section>
...
goto AFTER_SECTION; //unconditional jump.
FALSE_SECTION
<code for false section>
...
AFTER_SECTION
<code that follows the z?x:y construct>
...
The way we'll execute these jumps is to store the current state of the instructions array and constants array inside the constants array, along with some PUSH_C instructions to push those constants onto the stack, then well jump to those positions by restoring the state of the two arrays. We'll do this at two different points along the parse of the ?: construct; once at each jump.
To help explain how this is going to work, here are the COND_JMP and UNCOND_JMP instructions as they will be executed within the evaluate function. You can see that they pull their operands off the stack, just like every other operation does.
double evaluate( Expression_T* ep, double* parameters )
{
double stack[50];
int stktop = -1; int constantIndex = 0; int indx;
...
for( indx=0; indx < ep->instructionsLen; indx++ )
{
...
switch( instruction )
{
...
case UNCOND_JMP: assert( stktop >= 1 );
stktop -= 2; cndx = (int)stack[stktop+1]; indx = (int)stack[stktop+2]-1; break;
case COND_JMP: assert( stktop >= 2 );
stktop -= 3; if( not stack[stktop+1] ) { cndx = (int)stack[stktop+2]; indx = (int)stack[stktop+3]-1; }
break;
...
}
}
return stack[0]; }
To do all this, however, we're going to need a little more detail within the Expression_T structure.
typedef struct ExpressionStruct {
double *constants;
int constantsLen;
int cndx; int *instructions;
int instructionsLen;
int indx; const char* infix;
} Expression_T;
It should be obvious that as we call addConstant() and addInstruction() we are incrementing the cndx and indx members respectively.
expression:
-> t9
-> expression '?' expression : expression
int expression( Expression_T* ep )
{
if( not t9( ep ) )
return 0;
while( ltrim( &(ep->infix) ), '?' == *(ep->infix) )
{
int condJmpConstant;
int uncondJmpConstant;
condJmpConstant = ep->cndx; addConstant( ep, 0 ); addConstant( ep, 0 ); addInstruction( ep, PUSH_C ); addInstruction( ep, PUSH_C ); addInstruction( ep, COND_JMP );
ep->infix++ ; oldfix = ep->infix;
if( not expression( ep ) )
{
error( oldfix ); }
uncondJmpConstant = ep->cndx; addConstant( ep, 0 ); addConstant( ep, 0 ); addInstruction( ep, PUSH_C ); addInstruction( ep, PUSH_C ); addInstruction( ep, UNCOND_JMP );
ep->constants[condJmpConstant] = ep->cndx;
ep->constants[condJmpConstant+1] = ep->indx;
ltrim( &(ep->infix);
if( ':' != *(ep->infix) ) {
error( oldfix ); }
ep->infix++ ; oldfix = ep->infix;
if( not expression( ep ) )
{
error( oldfix );
}
ep->constants[uncondJmpConstant] = ep->cndx;
ep->constants[uncondJmpConstant+1] = ep->indx;
}
return True;
}
Pattern: You may have to write a good bit of "compiler" code within your "parser". I can't think of any way we could have fully accepted the ?: construct in one step, THEN gone back and filled in the details. We had to mix it up along the way.
The main() Routine
Any time you implement a compiler, and especially if you do it by hand as we have done the expression compiler, you should build a really good test suite. While I'm not going to discuss building it, I will say that it's a good idea to start by testing the simplest constructs first, and then slowly build upon success. The "main()" routine in the expression source contains the tests I implemented.
By the time I have software up and running, I usually have it just chock-full of debugging statements. I find the most effective debugging to be a combination of an interactive debugger (like Visual C++) AND a logfile generation mechanism. The logfile lets me quickly jump to the position in the execution where I'm trying to figure out what's going on. The expression.c source code is no different. The actual code (as opposed to the example code I've included in the article) is full of assertions and debugging code.
It's also a good idea when writing a test routine to NOT fill up the output screen on success, but rather to only throw error messages on actual errors. On my 3GHz machine, if I have full debugging output turned on, it takes about 7 seconds to output all the data from the test cases. On the other hand, if I have the debugging turned off, and ONLY ask it to run the internal tests (without tracing), it completes as quickly as I hit the return key. This is a whole lot better option in case someone wants to put a script together to run test suites on many different libraries.
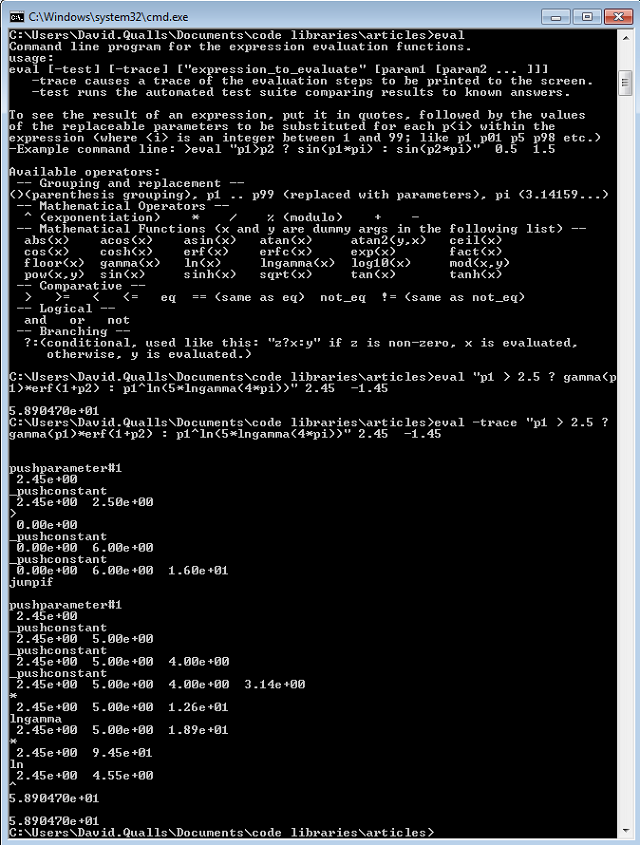
One thing that occurred to me during testing was that there is not a sure-fire way of determining HOW the expression system is going to compile any particular infix expression handed to it at run time. Here is the scenario: I put an expression into my .ini file, read it in, compile it, and HOPE that the expression compiler interprets it the same way I intended! Yes, I could write a separate program to read in the expression and compute it and compare against known outputs, but that seems a lot of work for the USER of these routines. Therefore, I included a section within the main() program that can be used interactively for just this purpose. Additionally, if someone is uncertain that the compiler is actually parsing the expression correctly, I included the "-trace" option to show the top few elements on the stack during evaluation, and how the operation is being performed. One can compare this against a hand-generated RPN version of the same expression.
I have found the test version of the program to be so useful for everyday work, that I renamed it "eval.exe" and put it in my path so I can call it from the command line. Now I use it regularly for quick little computations that I used to use the Windows "calc" program for, or would break open a spreadsheet for.
Summary (x2)
With careful consideration, and a simple enough grammar, the patterns identified in this article can be used to successfully roll your own recursive descent parser/compiler. Considering the time it takes to learn a compiler-compiler system, it MAY be a more effective use of your time to roll your own compiler than to learn a new system. I'd say that the complexity of the expression grammar implemented in this article is on the ragged edge of needing to break out a compiler-compiler.
Regardless of whether you roll your own, or use a compiler-compiler, you must CLEARLY UNDERSTAND what the compiler needs to do upon recognizing each production rule. The non-terminal function that implemented the branching construct (the "expression()" non-terminal above) should have been a good example of that principle. A compiler-compiler cannot help you with this. The compiler-compiler just helps you implement the grammar correctly, and get the production actions in the right place.
*Final Thoughts
*From the introduction paragraph: "...software magically evolves" (wink) when smart people are in the presence of patterns. Of course, WE know there's nothing magical about it: it's a lot of thought and hard work. But biological machines (living organisms), which are orders of magnitude more complex than any software or hardware ever seen, apparently do evolve without the benefit of any "smartness" (or intelligence) whatsoever. If we are to believe evolutionists, they just spring into existence by pure random chance.
I once heard a very smart programmer say that trusting things to chance was not a good way to write software. As a mechanical engineer myself, I can affirm that this principle also applies in machine design; randomly stringing mechanical-components together just doesn't cut it. Apparently, however, according to evolutionists, random chance works GREAT in biological design. Pure random chance composed not just any-old biological machine, but machines so complex that they can reproduce, and one of them is so sophisticated and intelligent that it even designs computers and writes software! Just unbelievable...
Hmmmm. A compiler-compiler "writes" software, kind-of mimicking the actions of a biological machine (it mimics the actions of those so-called "humans"). I'm thinking a really great compiler-compiler can be had by just randomly scrambling lots of instructions together. And hey, isn't that how YACC originally came about (but it evolved in the days of slower computers. Today, we have better random number generators and faster computers so this new compiler-compiler will be much smarter / more evolved).
I'M ON IT!<nbsp><nbsp>
<nbsp><nbsp>;-)
Have fun building YOUR compiler!
David Qualls
History
- 17th November, 2011: Initial version
- 5th December, 2011: Article updated
