Introduction
Ever wondered if some programming languages stereotypes like "Fortran is the fastest language" or "C++ cannot be matched by Java or C#" are still valid? This article tries to answer a part of this question. Evaluations have been done in the following languages:
- C#
- C++
- Java
- Fortran
- JavaScript
The last one was not meant as a serious competitor for the ones above rather than out of interest. The results of JavaScript will not be mixed up with the other four languages. Every language had several tests in order to find out other interesting details. Some of those details concerned:
- How much slower is Debug than Release for a C# application?
- How much acceleration do I get for (32-bit) integer operations due to 64-bit (instead of 32-bit)?
- Does it matter if a C# application is compiled for AnyCPU or x64?
- How much slower does a program get by compiling it to MSIL instead of direct bytecode?
- Which browser has the fastest JavaScript engine measured in cycles per operation?
In order to do those evaluations as realistic as possible, a code has been set up that will be explained later. It should be noted that the code was rewritten as exact as possible. Nevertheless, some languages did not provide equal features as the original program code, which was written in C#. Therefore other time measurement routines have been used for JavaScript, Java and Fortran since those languages do not offer a good connection to the Windows system and therefore cannot access the Windows system team measured in Ticks, where 1 Tick occurs every 1000 cycles.
What This Article is Good For
This article aims to give some qualitative comparison of the languages performance on the core operations such as the addition (+), subtraction (-), multiplication (*) and division (/) as well as modulo (%). Also combined operations like division, addition and modulo (/+%) and division, addition, subtraction and multiplication (/+-*) were tested. This will give us some insight about the optimizations of the used compiler. Every language depends hugely on the used compiler since a language is nothing more than a set of grammar rules and meaningful words. The compiler is responsible to use the given language in order to translate the code from a high-level to a lower level (like Assembler code or MSIL).
What This Article Is Not About
This article does not aim to give insight about peak performances of each language or compiler. Optimizations were used in a restrictive manner, such that the optimizations would never break any big code. Therefore I used O2 optimizations as a maximum level for Fortran or C++. Also I did not set up a complete new computer, i.e. some programs and services were running and active during the benchmarks. However, the CPU was at a low / medium load while doing the benchmarks, which is something that will also occur in real world applications. Therefore, I consider this a practical test.
This article will also not say that any language is faster than another language. In my opinion, the speed of language is determined by a lot of factors. Even if a language executes faster operations, it is not said that memory operations are also scaled like that. Also many programs access different resources (HDD, Network, ...) which may also favor different languages than the ones that are listed here. In total, the speed of a language for a certain kind of operation does not say too much about the performance of the language - every language targets a different class of problems.
Background
In order to calculate the optimal width of an item in a collection, I divide the width of the available space through the number of items. This is an integer division, i.e., we will get back an integer. In general, the result is not exact, i.e. if I multiply the result with the number of items, then I won't obtain the width of the available space again. In order to avoid such a mistake, I basically do the following:
int widthPerItem = total_width / items.Length;
int remaining = total_width % items.Length;
From this point on, we have two possible solutions. The first solution is not very elegant:
items[0].Width = widthPerItem + remaining;
for(int i = 1; i < items.Length; i++)
{
items[i].Width = widthPerItem;
}
Here we give the additional (remaining) pixels to the first item and leave the other items with the calculated width. The second solution is more elegant:
for(int i = 0; i < items.Length; i++)
{
items[i].Width = widthPerItem + Math.Sign(remaining);
if(remaining > 0)
remaining--;
}
Here, we add one pixel to the calculated width of each item until we have no more pixels. This means some items will get the calculated width plus one pixels, while the other items get just the calculated width. While those two solutions seem to fit in various situations, my article will deal with the initial problem of first doing a division followed by a modulo operation. Those two operations are about equally expensive. Both operations are really expensive as well! I was once told that a division is about eight times as expensive as an addition. This article will try to find out:
- Are the rules of thumb still valid?
- A subtraction is equal to an addition
- A multiplication is more expensive than an addition
- A division is about eight times as expensive as an addition
- A modulo operation is equal to a division
- Is the following code a better approach for retrieving the remaining part?
int widthPerItem = total_width / items.Length;
int remaining = total_width - widthPerItem * items.Length;
The Basic Code
The original code was written in C# for the .NET-Framework. In order to measure the performance, each operation had to be repeated multiple times. For the evaluation, we set the program to 10,000 repetitions. Since just repeating one operation in a for-loop can sometimes be solved trivially by the compiler, it was necessary to alter the operands. This was solved by using an array of data-points, with a quite long array length. We used 100,000 data-points. This results in an array size of 100,000 times 4 bytes (an integer), i.e. 400,000 bytes or about 391 kB. This is certainly bigger than the Level 1 cache of the processor but certainly smaller than the L2 cache of the processor (nowadays).
All in all, each operation (or combined operation) is executed 109 times. Since the usual frequencies are in the GHz or 109 Hz range, we can estimate that each loop will take longer than one second since every operation will require at least one cycle. The Stopwatch instance will give us the time in ticks, i.e. in 103 cycles. This will still result in quite large numbers, so we divide the result through 1000 in order to obtain the result in 106 cycles.
const int SIZE = 100000;
const int REPEAT = 10000;
static void Main(string[] args)
{
Random ran = new Random(0);
int[] A = new int[SIZE];
int[] B = new int[SIZE];
int[] C = new int[SIZE];
for (int i = 0; i < SIZE; i++)
{
A[i] = ran.Next();
B[i] = ran.Next();
}
Stopwatch sw = new Stopwatch();
sw.Start();
for (int j = 0; j < REPEAT; j++)
for (int i = 0; i < SIZE; i++)
C[i] = A[i] + B[i];
sw.Stop();
Console.WriteLine("+: " + sw.ElapsedTicks / 1000);
sw.Reset();
sw.Start();
for (int j = 0; j < REPEAT; j++)
for (int i = 0; i < SIZE; i++)
C[i] = A[i] / B[i] + A[i] % B[i];
sw.Stop();
Console.WriteLine("/ + %: " + sw.ElapsedTicks / 1000);
sw.Reset();
sw.Start();
for (int j = 0; j < REPEAT; j++)
for (int i = 0; i < SIZE; i++)
{
C[i] = A[i] / B[i];
C[i] += A[i] - C[i] * B[i];
}
sw.Stop();
Console.WriteLine("/ + -*: " + sw.ElapsedTicks / 1000);
}
One thing to remark here is that this is a real world evaluation. If we wanted to perform on peak performances, we would implement matrix vector products. No one could argue that in real world applications, one would first have to gather the operands from RAM or even hard-disk. However, this would make the evaluation even harder and less accurate, since RAM and hard-disk have a much higher access time than the operation would take. In such a case, it would be required to measure RAM or hard-disk access time independently and add it to the measurements of this evaluation.
The Benchmarks
Every benchmark included the 5 elementary operations and 2 combined operations. The following benchmarks were performed:
- C# with AnyCPU in Debug
- C# with AnyCPU in Release
- C# with x64 in Release
- C# with x86 in Release
- C++.NET AnyCPU in Debug (/CLI)
- C++.NET AnyCPU in Debug (/MSIL)
- C++.NET x64 in Release
- C++.NET x86 in Release
- C++ (MinGW) for x64
- C++ (MS) for x64
- Fortran (MinGW) for x64
- Java SDK7-x64 Release
All measurements have been performed in units of 106 cycles or have been performed in units of 10-3 seconds (milliseconds or short ms). Measurements using the later one have been recalculated to 106 ticks using the equation (where f is the clock-frequency of the CPU, i.e. cycles per second),
TTicks=f * TSeconds / 1000.
By using Ticks / s (which is cycles / ms) we can also use TMilliseconds in order to calculate the time in cycles. Since we want to compare 106 cycles, we have to divide the final result by 106. Those 106 cycles are then equivalent to 103 Ticks or Ticks in thousands. The final result of the first evaluation round is the following:
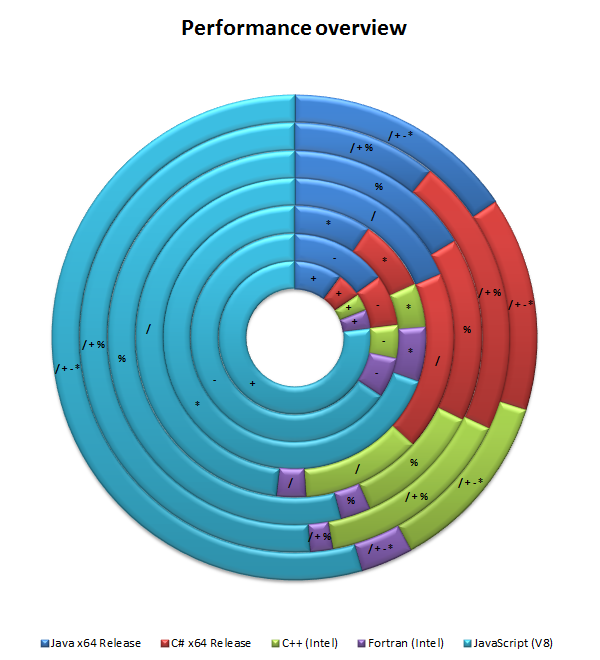
| | + | - | * | / | % | / + % | / + - * |
|---|
| C# | Any CPU, Debug | 19114 | 18686 | 19599 | 18916 | 18833 | 29893 | 37223 |
|---|
| Any CPU, Release | 2546 | 2638 | 2627 | 12341 | 12260 | 24269 | 12054 |
| x86, Release | 7743 | 7846 | 7630 | 12355 | 12072 | 26073 | 18906 |
| x64, Release | 2574 | 2555 | 2592 | 12486 | 12286 | 24324 | 12084 |
| C++ | Any CPU, /CLI, Debug | 11406 | 11795 | 11629 | 14681 | 14779 | 24347 | 31903 |
|---|
| Any CPU, /MSIL, Debug | 11563 | 11480 | 11514 | 14896 | 14698 | 24643 | 26446 |
| x86, Release | 3156 | 3337 | 3286 | 12575 | 12102 | 24939 | 12628 |
| x64, Release | 3850 | 3883 | 3969 | 13003 | 12846 | 24716 | 12855 |
| x64, mingw | 12522 | 12768 | 12773 | 15598 | 14572 | 24468 | 34050 |
| x64, ms | 3195 | 3196 | 3462 | 12828 | 12257 | 12132 | 12600 |
| Fortran | x64, mingw | 9324 | 9141 | 9361 | 12980 | 13857 | 26253 | 23328 |
|---|
| Java | jsdk7-x64 | 4929 | 4964 | 2800 | 12466 | 12565 | 12483 | 13057 |
|---|
| Best | 2546 | 2555 | 2592 | 12341 | 12072 | 12132 | 12054 |
|---|
Using the data, I could draw the following conclusions:
- The debug mode is really slow - this is due to the Visual Studio Hostprocess being attached to every operation.
- C# is a language that really benefits from 64-bit - the compiler seems to be able to increase speed compared from x86 to x64.
- There is no difference between x64 and AnyCPU (on my x64 system). Therefore compiling to AnyCPU seems to be the best option unless you want to restrict your program to a certain architecture or Framework. One example where this makes sense is if you want to use the x86 Version of the .NET-Framework - even on x64 Systems.
- The GNU compiler did not perform well at all. This seems to confirm the common stereotype that the GNU compilers are not suitable for HPC usage.
- Some intelligent compilers are also present - that can be seen by the fact that the naive (/ + %) operation requires the same cycles as the optimized version (/ + - *). This is only possible if the former one is translated to the later one automatically. The Java compiler and the Microsoft (C++) compiler did a very good job here.
- In debug mode, the only number that counts is the number of operations since the attachment of the Visual Studio Hostprocess costs more than the operation itself. This means that each operation costs about the same (and more than the operation itself) and scales with the number of operations.
- C# proves to be really solid winning nearly all.
The data resulted in the following chart:

It is also worth noting that I performed several JavaScript benchmarks on all major browsers:
- JavaScript in V8 (Chrome 15)
- JavaScript in Chakra (IE 9)
- JavaScript in Carakan (Opera 11.52)
- JavaScript in SpiderMonkey (Firefox 8)
- JavaScript in Nitro (Safari 5.1.1)
| | + | - | * | / | % | / + % | / + - * |
|---|
| JavaScript | V8 (Chrome) | 37274 | 21633 | 20543 | 32485 | 41556 | 58794 | 45791 |
|---|
| Chakra (IE) | 38424 | 38103 | 122998 | 143617 | 53781 | 231479 | 314839 |
| Carakan (Opera) | 66330 | 66426 | 68589 | 79509 | 68092 | 137450 | 165267 |
| SpiderMonkey (Firefox) | 49405 | 51231 | 51868 | 80634 | 195912 | 222444 | 105849 |
| Nitro (Safari) | 52014 | 51508 | 86761 | 69356 | 52750 | 99713 | 148745 |
| Best | 37274 | 21633 | 20543 | 32485 | 41556 | 58794 | 45791 |
|---|
Using the data, I could draw the following conclusions:
- All JavaScript engines perform worse than C++.
- Compiling to bytecode gives Google Chrome's V8 engine a huge boost compared to other engines.
- The other engines perform as other languages perform in debug mode - this is due the interpretation process. The browser is attached to the JavaScript code and therefore performs an interpretation step before and after each operation. This means that the operation itself does not matter - only the number of operations matter.
- A general statement might be: If you have the choice between doing something optimized - but with more operations - and naive (or less optimized) you should stick with the later one.
- The IE engine does have some problems with multiplication and division. The problem does not occur with modulo.
- Modulo seems to be implemented in a special way since all interpretation engines excluding Firefox show a better result here than with a division.
The data resulted in the following chart:

Additionally, I had the chance to do another interesting set of tests with high-performance compilers provided by Intel. These tests ran on another (special) machine, so it would have been unfair to compare those results with the ones from the benchmark above. These benchmarks included:
- Fortran (Intel) for x64
- C++ (Intel) for x86
- C++ (Intel) for x64
- C++ (MS) for x86
- C++ (MS) for x64
All those additional benchmarks were executed with the optimization level set to O2. This was also very effective for Fortran, since O3 crashed always and parallel mode or SSE3 optimized modes proofed to be even slower than a plain O2 optimization.
| | + | - | * | / | % | / + % | / + - * |
|---|
| Fortran | x64 - Intel | 1976 | 2025 | 1975 | 2024 | 2026 | 1973 | 2987 |
|---|
|
| C++ | x86 - Microsoft | 3045 | 3107 | 2974 | 8450 | 8449 | 8427 | 8594 |
|---|
| x64 - Microsoft | 2469 | 2422 | 2441 | 8359 | 8357 | 8395 | 8390 |
| x86 - Intel | 1852 | 1739 | 1876 | 9529 | 10156 | 18861 | 11644 |
| x64 - Intel | 1724 | 1723 | 1586 | 8196 | 8597 | 17427 | 10235 |
| Best | 1724 | 1723 | 1586 | 2024 | 2026 | 1973 | 2987 |
|---|
Using the data, I could draw the following conclusions:
- Fortran does obviously do a lot of cool optimizations.
- While Fortran seems to be slower on simple operations like addition, subtraction and multiplication it certainly is superior in more advanced or combined operations.
- Intel seems to know (their) hardware better (Ah, really?!) while Microsoft seems to know (their) software, i.e. a compiler or programming language, better. This can be seen by looking at the optimizations done by the Microsoft compiler in order to reach the same level with the naive operation (/ + %) as with the optimized operation (/ + - *).
The data resulted in the following chart:

Evaluations
The computer that was used for the primary benchmarks has the following specifications:
- Intel Core2Duo CPU
- Clock frequency 2343808 kHz
- 6 GB of RAM
- Windows 7 x64
The other computer which had the Intel compiler installed has the following specifications:
- Intel Core2Duo CPU
- Clock frequency 3247109 kHz
- 8 GB of RAM
- Windows 7 x64
I used the following environments in order to evaluate the different code files:
- All C++.NET, C++ with the Microsoft compiler, C++ / Fortran with the Intel compiler and C# evaluations have been done using Microsoft Visual Studio 2010 with Service Pack 1.
- C++ / Fortran with the MinGW compiler have been compiled using the command line.
- Java has been compiled and evaluated using IntelliJ IDEA.
For evaluation purposes, I rewrote the original C# code to other platforms. The major differences for the different languages and platforms (.NET, Windows, Browser, ...) are outlined in the code snippets below:
The C++.NET version was certainly quite close to the C# version in terms of the Random class as a random number generator. Also the Stopwatch class could be used.
#include "stdafx.h"
#define SIZE 100000
#define REPEAT 10000
using namespace System;
using namespace System::Diagnostics;
int main(array<System::String ^> ^args)
{
int* A = new int[SIZE];
int* B = new int[SIZE];
int* C = new int[SIZE];
Random^ ran = gcnew Random(0);
for (int i = 0; i < SIZE; i++)
{
A[i] = ran->Next();
B[i] = ran->Next();
}
Stopwatch^ sw = gcnew Stopwatch();
sw->Start();
for (int j = 0; j < REPEAT; j++)
for (int i = 0; i < SIZE; i++)
C[i] = A[i] + B[i];
sw->Stop();
Console::WriteLine(L"+: " + sw->ElapsedTicks / 1000);
sw->Reset();
}
The transition from C++.NET to C++ (Windows API) was not very complicated. However, it was necessary to a custom class to mimic the behaviour of the .NET-Stopwatch class. I wrote my own Stopwatch containing all the methods of the original version and using the Windows API in order to retrieve the current tick count.
#include <stdio.h>
#include <stdlib.h>
#include <windows.h>
#include <iostream>
#define SIZE 100000
#define REPEAT 10000
using namespace std;
class Stopwatch
{
LARGE_INTEGER start;
LARGE_INTEGER end;
public:
Stopwatch()
{
LARGE_INTEGER frequency;
QueryPerformanceFrequency(&frequency);
cout << "Frequency: " << frequency.QuadPart <<
" Ticks/s" << endl;
Reset();
}
long ElapsedTicks;
void Reset()
{
ElapsedTicks = 0;
}
void Stop()
{
QueryPerformanceCounter(&end);
ElapsedTicks = end.QuadPart - start.QuadPart;
}
void Start()
{
QueryPerformanceCounter(&start);
}
};
int main()
{
int* A = new int[SIZE];
int* B = new int[SIZE];
int* C = new int[SIZE];
srand(0);
for (int i = 0; i < SIZE; i++)
{
A[i] = rand() + 1;
B[i] = rand() + 1;
}
Stopwatch* sw = new Stopwatch();
sw->Start();
for (int j = 0; j < REPEAT; j++)
for (int i = 0; i < SIZE; i++)
C[i] = A[i] + B[i];
sw->Stop();
cout << "+: " << sw->ElapsedTicks / 1000 << endl;
sw->Reset();
}
Java (to my surprise) did also not include a Stopwatch class to be used. This might make sense since Java does also not know anything about Ticks, since Java aims to be platform independent and Ticks is a concept that was mostly used in Windows. So I used an already build Stopwatch instance and extended it with an automatic conversation into Ticks (this conversation is specific to my computer - so if you want to use it, you should alter the line in the code with your frequency in Ticks / s or with the general clock frequency / 1000).
public class Stopwatch {
private long startTime = 0;
private long stopTime = 0;
private boolean running = false;
public void start() {
this.startTime = System.currentTimeMillis();
this.running = true;
}
public void stop() {
this.stopTime = System.currentTimeMillis();
this.running = false;
}
public void reset() {
startTime = 0;
stopTime = 0;
}
public long getElapsedTime() {
long elapsed;
if (running) {
elapsed = (System.currentTimeMillis() - startTime);
}
else {
elapsed = (stopTime - startTime);
}
return elapsed;
}
public long getElapsedTicks() {
double frequency = 2343808;
return (long)((((double)getElapsedTime()) / 1000.0) * frequency);
}
public long getElapsedTimeSecs() {
long elapsed;
if (running) {
elapsed = ((System.currentTimeMillis() - startTime) / 1000);
}
else {
elapsed = ((stopTime - startTime) / 1000);
}
return elapsed;
}
}
Using the custom Stopwatch class, I could write the following program:
import java.util.Random;
public class Main
{
final static int SIZE = 100000;
final static int REPEAT = 10000;
public static void main(String[] args)
{
Random ran = new Random(0);
int[] A = new int[SIZE];
int[] B = new int[SIZE];
int[] C = new int[SIZE];
for (int i = 0; i < SIZE; i++)
{
A[i] = ran.nextInt();
B[i] = ran.nextInt();
}
Stopwatch sw = new Stopwatch();
sw.start();
for (int j = 0; j < REPEAT; j++)
for (int i = 0; i < SIZE; i++)
C[i] = A[i] + B[i];
sw.stop();
System.out.println("+: " + sw.getElapsedTicks() / 1000);
sw.reset();
}
}
The biggest change was certainly done by using Fortran. Fortran does not start the index of an array at 0 but at 1. Also Fortran uses regular (round) brackets instead of square brackets to talk to an index of an array. Also in order to be backwards compatible, it is required to write Fortran is the original way, i.e., using a very old style of programming with punched cards. This means that the program has to fulfill certain requirements such that the first six columns are specially handled by the compiler. Also the maximum length of a row cannot exceed 80 columns, with the last 8 columns being reserved for comments.
PROGRAM MEASUREMENT
INTEGER s
INTEGER A (100000), B (100000), C (100000)
INTEGER r
INTEGER i, j
s = 100000
r = 10000
C Those two are being used for the relative time measurements
REAL TIMEARRAY (2)
REAL DELAPSE
C Initializes the random number generator with a seed
CALL srand(0)
C Filling the vectors with random numbers
do i = 1, s
A(i) = 10 * rand(0) + 1
B(i) = 10 * rand(0) + 1
enddo
DELAPSE = DTIME(TIMEARRAY)
do j = 1, r
do i = 1, s
C(i) = A(i) + B(i)
enddo
enddo
DELAPSE = DTIME(TIMEARRAY)
WRITE (*,*) '+: ', DELAPSE
C More evaluations
END PROGRAM
The evaluation in JavaScript was quite fast to write. Also like Java JavaScript does not provide a certain routine to test the time. Testing the time can result in quite inexact results - depending on the browser. However, considering the length of the test it is obvious that deltas in time measurements as the 15 ms of (older?) Internet Explorer will not matter too much in this case, since the time will certainly be in the seconds (or even minutes) area.
var SIZE = 100000;
var REPEAT = 10000;
var A = new Array(SIZE);
var B = new Array(SIZE);
var C = new Array(SIZE);
for (var i = 0; i < SIZE; i++)
{
A[i] = parseInt(Math.floor(Math.random() * 100001)) + 1;
B[i] = parseInt(Math.floor(Math.random() * 100001)) + 1;
}
function benchmark(f, id) {
var start = (new Date).getTime();
f();
var diff = (new Date).getTime() - start;
document.getElementById(id).innerHTML = diff;
}
function plus() {
for (var j = 0; j < REPEAT; j++)
for (var i = 0; i < SIZE; i++)
C[i] = A[i] + B[i];
}
It should be said that the JavaScript has to be converted to Ticks / s manually afterwards. If you run this evaluation, then please build use something like the following or convert it afterwards:
function benchmark(f, id) {
var start = (new Date).getTime();
f();
var diff = (new Date).getTime() - start;
document.getElementById(id).innerHTML = parseInt(time2Ticks(diff) / 1000);
}
function time2Ticks(msec) {
var frequency = 2343808;
return msec / 1000 * frequency;
}
Using the Code
The code can be used without any limitations. If you have suggestions for improvements or ideas for further evaluations, you are welcome to comment here. It should be noted that I thought about doing the same evaluations on Linux, but skipped that because I thought it would be unfair to test a fresh system against a system that is running since some years and is loaded with some services and many programs in the background. Also the Microsoft compiler is not available on Linux leading to a different evaluation in this scope. For C#, I would have used the Mono implementation. However, you are welcome to make a similar evaluation on a Linux machine and inform me about the results. As long as the results are in Cycles / operation or Ticks / Operation, it is kind of comparable (again: the thing which makes it unfair to compare is the background load of the system, i.e. the programs and services that require some cycles to be executed while the (benchmark) program is running).
In order to get Fortran running, we used the following compilation command (this is obviously executing O2 optimizations against our code):
$ ifort base.f /check:bounds
All the required codefiles are included in the source.zip file.
Bonus: Scripting languages
Another interesting evaluation can be done in the scripting languages genre. Here I included the following languages:
- Perl (ActiveStatePerl for Windows 5.14.2 x64)
- PHP (Version 5.3.1 for Windows, which was included in the XAMPP)
- Python (Version 2.5.4 for Windows)
First: Please note that the version of Python is obviously outdated. I do not know if newer version provide a better performance. I did not hear about better performance, but if I'll ever have the time to change the Python installation on my computer I will do another evaluation for sure. The next thing to notice is that I did run all those benchmarks on Windows. PHP is getting faster and faster on Windows, however, I do think that it is still faster on Linux than on Windows. This is obviously also true for the other two scripting languages, since they have their origins in the Linux operating system as well.

PHP seems to be faster than Perl due to various factors. On the one hand it is a specialized version of Perl, on the other side it has been regularly maintained in the last decade. It is also worth noting that there is a certain Windows factor in this evaluation. I would be curious to see this evaluation on Linux (and I will either do that myself sometimes in the future or wait for somebody to post reliable results). Either way, it is quite obvious that the scripting languages are really slow. I actually thought that they might be even slower than JavaScript, but a factor of 20 is quite a surprise. It is also worth noting that all those languages are following the pattern as seen from other scripting languages, containing the costly interpretation steps between the operations.
All in all I do think that this kind of evaluation is kind of unfair. The scripting languages were never supposed to care about operations - they should provide a reliable and easy to use source for quick and dirty programming. The evaluation is unfair since the for-loop is in my opinion too heavy and does require too many operations to be performed. The languages presented before (which have been the original target of the article) do contain special treatment for such loops. Therefore the time spent performing the loop itself is neglectable compared to the operation. This is what we were up to. Now this is not the case. I believe that all languages are direct proportional to the number of operations performed - including conditions, loop counters and others.
This is true if have a close look at the following numbers:
| | + | - | * | / | % | / + % | / + - * |
|---|
| Script Languages | Python | 913839 | 945178 | 976808 | 942330 | 989024 | 1572805 | 2200857 |
|---|
| Perl | 787519 | 796895 | 794551 | 803926 | 820333 | 1335971 | 1999268 |
| PHP | 637516 | 637516 | 639860 | 665641 | 672673 | 1024244 | 1258625 |
| Best | 637516 | 637516 | 639860 | 665641 | 672673 | 1024244 | 1258625 |
The best values are provided by PHP which is linear dependent on the number of operations. We have three to six dominant operations (the inner loop counter increment, the inner loop condition and the number of operations which is ranging from atomic like + to complex / + - *). Therefore every operation is about 200 cycles of computation time, which is about 70 times as expensive as C#. Perl and Python might do some other operations internally, which is why the linear behaviour cannot be applied here. However, we do see that the number of operations scales with the computation time, which is still characteristic for such languages. Here writing something in a simple way performs better than trying to squeeze some performance out of the computer by using more operations in a more complex algorithm.
Update: JavaScript Performance
I was a bit disappointed after my first JavaScript performance evaluation. The browser vendors were marketing the new JavaScript possibilities of their products quite enthusiastically. However, the real performance was really slow compared to C++ (besides Google's V8 engine). Now I changed my opinion after doing these benchmarks on the most popular scripting languages. Since JavaScript is still (again: besides Google's V8 engine) a scripting language, it is remarkable how much performance the browser vendors could squeeze out. And according to reports they are still working on improvements for providing even faster JavaScript.
So I took the opportunity to have a close look at the recent versions of the five most popular browsers (compare with the listings above):
- JavaScript in V8 (Chrome 16)
- JavaScript in Chakra (IE 10 PP2 since PP4 is only available for Windows 8 DP)
- JavaScript in Carakan (Opera 11.6)
- JavaScript in SpiderMonkey (Firefox 9)
- JavaScript in Nitro (Safari 5.1.2)
Here bold numbers indicate a change. Since another table of data is too much I will just highlight the changes:
- V8 is still being enhanced. All evaluations remained constant with exception of the last (combined) benchmark. Google Chrome 16 saves about 25% of computation time there. I suppose the compiler now recognizes some patterns and performs some optimizations on these.
- IE did not change at all from the release version 9 to the platform preview of version 10. I think most of the performance upgrades have not been done in JavaScript but in the DOM manipulation and DOM rendering process.
- Opera did not change at all.
- Firefox made a huge leap. More on that below!
- Safari remains the same - maybe a little bit slower, but the difference is not significant.
Firefox 9 did not contain any spectacular features - one might think. However, under the surface the guys at Mozilla seem to have a done a pretty good job on improving the JavaScript engine. Firefox 9 now executes JavaScript operations about twice as fast as Firefox 8. The first benchmark (addition) is even the faster than Google V8 and the only winner in this JavaScript benchmark that is not called Google V8. The data from Firefox (the complete data can be viewed in the included sheet):
| | + | - | * | / | % | / + % | / + - * |
|---|
| Mozilla Firefox | 9 | 23956 | 24385 | 29424 | 55152 | 39906 | 76924 | 83547 |
|---|
| 8 | 49405 | 51231 | 51868 | 80634 | 195912 | 222444 | 105849 |
| Ratio 9 to 8 | 48% | 48% | 57% | 68% | 20% | 35% | 79% |
The Mozilla team did a really good job in improving their JavaScript engine. In the following chart we can also see that Google is still working on improvements for their JavaScript engine V8. It will be interesting into what kind of regions JavaScript will be pushed the next years. The next chart contains the ratio of the current performance vs the former performance, i.e. a value lower than 100% means an improvement. Values around 100% are usually equivalent in performance, since a small number of the evaluation is being determined by the current state of the computer and other factors.

Conclusion
In general, it is safe to say that a subtraction is equal to an addition, which is equal to a multiplication. A division is about five times as expensive as an addition and is equal to a modulo operation. Fortran executes division and modulo operations more efficiently, leading to a faster execution.
In general, the optimized version of the operation (% + - *) should be preferred over the naive one (% + / ). This statement breaks for interpreted scripting languages where the operations cost much more due to interpretation steps. Therefore in JavaScript, the best performance can be reached by the straightest solutions - skipping operations which would lead to optimizations in other languages.
Points of Interest
Writing the test program in all those different languages was quite funny. I did not write Fortran in a long time and was astonished that the language itself still feels really old and outdated. However, the performance is still unmatched in some key fields like divisions. I cannot imagine that this is something which could be only implemented in compilers for Fortran, so I wonder why other compilers do still not have similar features yet.
I was also amazed how strong Google's V8 JavaScript engine performed. When Chroma did come out, I used it for a while until I found myself being in love with Opera's independent browser. Now this performance test showed that the developers did not lie about the core feature of V8 - direct compilation into bytecode for the provided JavaScript code. Of course, this is something very cool for webpages, however, it should be noted that arithmetic operation time is usually not the key aspect of JavaScript code since JavaScript is not being used in HPC. Most operations in JavaScript code are DOM manipulations or other interactions with the browser. Therefore this benchmark does also not state that Google Chrome is the best browser or fastest browser for JavaScript. Nevertheless, I assume that Chrome won't perform too bad in DOM manipulations either.
References
I found the following links useful:
- Article on StackOverflow about using Windows API to retrieve the tickcount.[^]
- Corey Goldberg's Stopwatch class for Java.[^]
- Doing relative timing in Fortran.[^]
- How to measure the absolute time in Fortran.[^]
- John Resig about the accuracy of JavaScript timing.[^]
History
- v1.0.0 | Initial release | 23.12.2011
- v1.1.0 | Update (Included major scripting languages and a JavaScript update) | 17.01.2012
