Introduction
Refer to http://en.wikipedia.org/wiki/Electrocardiography for an understanding of ECG signal and leads. Conventionally such ECG signals are acquired by ECG acquisition devices and those devices generate a printout of the lead outputs. A cardiologist analyzes the data for checking the abnormality or normalcy of the signal. But in recent times, automatic ECG processing has been of tremendous focus. http://www.codeproject.com/KB/cpp/ecg_dsp.aspx gives a fantastic overview of acquiring and filtering ECG signals through inexpensive hardware into your PC. You can download ECG signal samples of various diseases from http://www.physionet.org/physiobank/database/mitdb/. Now the main point of concern is how to develop a system for extracting the features from ECG signal so that these features can be used for Automatic Diseases Diagnosis. In this Article we shall discuss a technique for extracting features from ECG signal and further analyze for ST-Segment for elevation and depression which are symptoms of Ischemia. You can Learn more about Cardio Vascular Abnormalities and their correlation with ECG peaks fromhttp://circ.ahajournals.org/content/110/17/2721.full.
Background
We will discuss about the algorithm in detail which process the ECG signal Obtained from MIT-BIH database and are in .mat format. For the current analysis, we consider signal of both Normal Sinus Rhythm and ST-Elevated signals. Finally Using a threshold we check the normalcy of the signals.
Using the Code
First Select a filename in .mat format and load the file.
[fname path]=uigetfile('*.mat');
fname=strcat(path,fname);
load(fname );
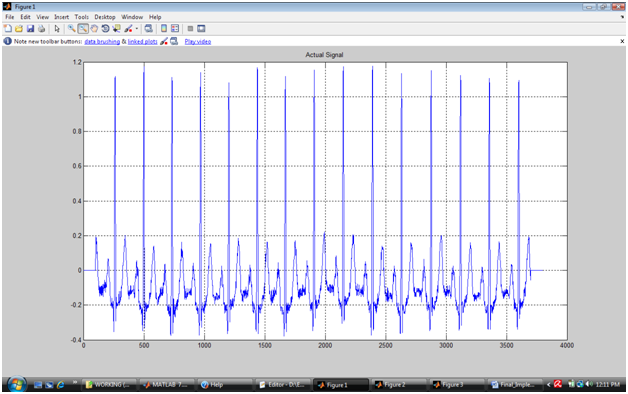
Append 100 zeros before and after the signal to remove the possibility of window crossing the signal boundaries while looking for peak locations.
z=zeros(100,1);
A=[z;A;z];
Perform wavelet decomposition. The process of wavelet decomposition down samples the signal. Which essentially means taking the samples at a much lower frequency than the orifinal signal. Therefore details are reduced and QRS complex is preserved.
[c,l]=wavedec(s,4,'db4');
Extract the Coefficients after the transform
ca1=appcoef(c,l,'db4',1);
ca2=appcoef(c,l,'db4',2);
ca3=appcoef(c,l,'db4',3);
ca4=appcoef(c,l,'db4',4);

If you plot the coefficients you will observe that the frequency bands are separated and ca1,ca2,ca3 and ca4 are cleaner signal. But they will have less number of samples than the actual signal due to downsampling. You can see that first signal resembles to the actual signal but has exactly one forth number of samples because the signal was decomposed in 4 levels. 2nd level has exactly half number of samples that of 1st level, 3rd level has exactly half number of samples than the 2nd level. Because the number of samples is reduced, such signals are also called down-sampled signal.
It is clear that 2nd level decomposed data is noise free. Therefore we consider this signal as ideal ECG signal from which QRS must be detected. But the first R is located in 3rd level decomposition signal at approximately 40th sample whereas the same is located in the original signal at 260th location. Therefore once R peak is detected in 3rd level reconstructed signal, it must be cross validated in the actual signal
Detecting R peak in the down sampled Signal
First find the values which are greater than 60% of the max value of the actual signal. Invariably these are R peaks. As the decomposed signals are noise free signals, First R peak needs to be detected in the Noise free signal. But remember the ultimate goal is to detect the Peak in the original Signal. The sample values in Original Signal will be different than the decomposed signal. So Our strategy here will be to first detect the R peaks in the down sampled signal and than cross verify those points the actual signal.
Let y1 be the decomposed signal.
m1=max(y1)*.60;
P=find(y1>=m1);
So P is now set of points which satisfies the above criteria. If you observe the signal very closely, R-Peak is not a single Impulse peak, therefore there are chances of multiple points in the same peak satisfying the criteria. One thing to remember is in 500Hz sampled signal No to R-Location will be found below 350 samples. In 4th Level decomposition order this value is around 20. So first we will remove the R locations that are too close.
P1=P;
P2=[];
last=P1(1);
P2=[P2 last];
for(i=2:1:length(P1))
if(P1(i)>(last+10))
% In this step we find R peaks which are atleast 10 samples apart
last=P1(i);
P2=[P2 last];
end
end
Now Variable P2 represents the position of R-Peaks in the down sampled signal.
Detecting R peak in the Original Signal
Search for the position of all the location in signal y1 which are greater than this value m1. They are R locations. But before we proceed, you must know that A R Location in Rt is at least 1/4th of the actual R location of the same point. Hence we will first map the detected positions to original signal by first multiplying with 4.
P3=P2*4;
%Multiply the current location with 4 to get the actual scale.
Another important thing you must remember is that, R location in down sampled signal will never be on the original signal at a scale of 4. Down sampling process always deviate the signal positions. Hence we need to search for the maximum value in the Original Signal in a window of +-20 samples from the reference R point obtained as P3.
Rloc=[];
for( i=1:1:length(P3))
range= [P3(i)-20:P3(i)+20]
%Search within a window of +-20 samples in the original signal with reference to up scaled R locations detected in downsampled signal.
m=max(A(range));
l=find(A(range)==m);
pos=range(l);
Rloc=[Rloc pos];
end
Ramp=A(Rloc);
It is clear now that Ramp and Rloc represents the R peak amplitude and location at the original scale. Let us see the marking of the same in the waveform.

Detecting Other Peaks With Reference to R-Peaks
From R-Peak Traverse Forth and Back and Search for Minima and Maxima, these are P,Q,T,S peaks respectively. So loop in Rloc and search for the other peaks.
Firstly, If you observe the waveform, it will be very clear that from R location if you select a window of Rloc-100 to Rloc-50 and find the maximum, than that maxima is P peak.
X=Rloc;
y1=A;
for(i=1:1:1) % If you have a 12 lead data than, for(i=1:1:12)
for(j=1:1:length(X))
a=Rloc(i,j)-100:Rloc(i,j)-10;
m=max(y1(a));
b=find(y1(a)==m);
b=b(1);
b=a(b);
Ploc(i,j)=b;
Pamp(i,j)=m;
%The minima in the Window of Rloc-100 to Rloc-10 is essentially the Q peak.
%% Q Detection
a=Rloc(i,j)-50:Rloc(i,j)-10;
m=min(y1(a));
b=find(y1(a)==m);
b=b(1);
b=a(b);
Qloc(i,j)=b;
Qamp(i,j)=m;
%With similar logic you can detect the S and T peaks.
%% S Detection
a=Rloc(i,j)+5:Rloc(i,j)+50;
m=min(y1(a));
b=find(y1(a)==m);
b=b(1);
b=a(b);
Sloc(i,j)=b;
Samp(i,j)=m;
%% T Peak
a=Rloc(i,j)+25:Rloc(i,j)+100;
m=max(y1(a));
b=find(y1(a)==m);
b=b(1);
b=a(b);
Tloc(i,j)=b;
Tamp(i,j)=m;
end
end
Once All the peaks are correctly detected, you can find the Onset and Offset as points of zero crossing for each lead. ST Segment can be calculated from S-Offset and T-Onset.
Points of Interest
You could also consider cleaning the ECG signal before processing using Symlet or any other filtering technique.
