Introduction
This article shows how to use a Fast Fourier Transform (FFT) algorithm to calculate the fundamental frequency of a captured audio sound. Also, we will see how to apply the algorithm to analyze live sound to build a simple guitar tuner: the code provides a solution to the problem of calculation of the fundamental frequency of the played pitch.
Background
The computer can capture live sound/music using a microphone that is connected to the sound card. Modern sound cards can capture digital signals. A digital signal is a set of quantized sound values that were taken in uniformly spaced times. The digital signal does not provide any information about frequencies that are present in the sound. To determine that, the data need to be analyzed.
The Short-Time Fourier Transform (STFT) makes representation of the phase and magnitude of the signal. The result of the STFT can be used to produce the spectrogram of the signal: the magnitude squared over time and frequencies. We will use a Fast Fourier Transform (FFT) to generate the spectrogram of the signal of short periods of time. After the spectrogram is calculated, the fundamental frequency can be determined by finding the index of the maximum value of the magnitude squared. The improved algorithm finds several such places, candidate frequency bins, with the magnitude squared in the top of the maximum values, and further analyzes them to verify the candidate fundamental frequencies by using the signal data.
When a note is played on a musical instrument, the sound waves are generated by strings, air, or the speaker - an instrument generates a musical note. One of the characteristics of a musical note is a pitch (fundamental frequency). Traditionally musical alphabet frequencies are divided by octaves, and then by semitones. An octave has 12 named pitches: C (prime), C#, D, D#, E, F, F#, G, G#, A, A#, and B. Octaves also have names: great, small, one-lined, two-lined, etc. The "standard pitch" (A one-lined or A4) has a fundamental frequency of its sound waves equals to 440 Hz. The frequencies of two neighboring notes are different by 21/12, and frequencies of the notes with the same name in two neighboring octaves are different by 2.
Table: Notes and Their Fundamental Frequencies
| Note Name | Traditional Octave Names (Scientific), Hz |
|---|
| Great (2) | Small (3) | One-lined (4) | Two-lined (5) |
|---|
| C | 65.4064 | 130.8128 | 261.6256 | 523.2511 |
| C# | 69.2957 | 138.5913 | 277.1826 | 554.3653 |
| D | 73.4162 | 146.8324 | 293.6648 | 587.3295 |
| D# | 77.7817 | 155.5635 | 311.1270 | 622.2540 |
| E | 82.4069 | 164.8138 | 329.6276 | 659.2551 |
| F | 87.3071 | 174.6141 | 349.2282 | 698.4565 |
| F# | 92.4986 | 184.9972 | 369.9944 | 739.9888 |
| G | 97.9989 | 195.9977 | 391.9954 | 783.9909 |
| G# | 103.8262 | 207.6523 | 415.3047 | 830.6094 |
| A | 110.0000 | 220.0000 | 440.0000 | 880.0000 |
| A# | 116.5409 | 233.0819 | 466.1638 | 932.3275 |
| B | 123.4708 | 246.9417 | 493.8833 | 987.7666 |
The typical (six string) guitar normally plays pitches of great through two-lined octaves. The pitches of the open strings (E2, A2, D3, G3, B3, and E4) are selected in the table in bold.
Using the Code
The solution contains three projects: the main windows application (FftGuitarTuner), the sound analysis library (SoundAnalysis), and the sound capture library (SoundCapture). The heart of the solution and the SoundAnalysis project is the FFT algorithm (see the Calculate method of the SoundAnalysis.FftAlgorithm class):
ComplexNumber[] data = new ComplexNumber[length];
for (int i = 0; i < x.Length; i++)
{
int j = ReverseBits(i, bitsInLength);
data[j] = new ComplexNumber(x[i]);
}
for (int i = 0; i < bitsInLength; i++)
{
int m = 1 << i;
int n = m * 2;
double alpha = -(2 * Math.PI / n);
for (int k = 0; k < m; k++)
{
ComplexNumber oddPartMultiplier =
new ComplexNumber(0, alpha * k).PoweredE();
for (int j = k; j < length; j += n)
{
ComplexNumber evenPart = data[j];
ComplexNumber oddPart = oddPartMultiplier * data[j + m];
data[j] = evenPart + oddPart;
data[j + m] = evenPart - oddPart;
}
}
}
double[] spectrogram = new double[length];
for (int i = 0; i < spectrogram.Length; i++)
{
spectrogram[i] = data[i].AbsPower2();
}
The data for the algorithm is provided from the sound card capture buffer. The abstract SoundCapture.SoundCaptureBase utility class is an adapter for DirectSound's Capture and CaptureBuffer classes, that helps to encapsulate buffering and setting up the audio format parameters. The application requires Microsoft DirectX 9 runtime components for the live sound capture from the microphone.
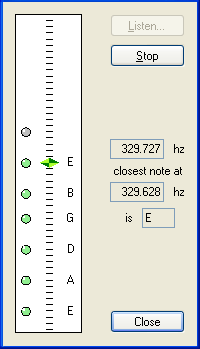
Figure: Main Application Form
After the application is started, select the sound device and play a note. The application will capture the live sound and will calculate the current fundamental frequency of the signal. The information can be used to tune the guitar.
Points of Interest
To calculate the Fast Fourier Transform, the Cooley-Tukey algorithm was used. It gives good performance for the required task. To challenge the algorithm, the application analyses about 22,000 sample blocks in real time: the sound is captured at a 44,100 Hz rate and a 16 bits sample size, and the analysis is performed twice a second.
The sound analysis library can be used for tone, background noise, sound, or speech detection. Series of the spectrogram of the continued sound can be displayed as a 2D (or 3D) image to present it visually.
References
- "Musical Note", Wikipedia
- "Short-Time Fourier Transform", Wikipedia
- "Fast Fourier Transform", Wikipedia
- "Cooley-Tukey FFT Algorithm", Wikipedia
History
- 1st January, 2009: Initial version
- 2nd January, 2009: Added algorithm code snippet
- 3rd August, 2010: Corrected article typos; new frequency detection algorithm
