Introduction
From Wikipedia:
A finite state machine (FSM) or finite state automaton (plural: automata) or simply a state machine, is a model of behavior composed of a finite number of states, transitions between those states, and actions. A finite state machine is an abstract model of a machine with a primitive internal memory.
Using the Code
In this article, I will focus on Moore machines. The easiest way to understand Moore FSA is to analyze its graph.
Example 1

- Symbols in the circles are states and they make up a set
{q0, q1}. Every state must have a unique symbol. - Labels written by every state
{y0, y1} describe data which is generated when the machine enters the state. - The arrows represent transitions between states. The
{z0, z1} set can also be called an "input alphabet".
Concluding, a Moore FSA is composed of states with assigned output symbols and transitions between those states. A Moore FSA is a specific case of definition from Wikipedia.
Let's find out how it works. If we were in the q0 state, then sending z0 signal would not change anything -- we would stay in the same place and repeatedly produce y0 (check it on the graph!). However, sending z1 would move us to the q1 state and produce y1. Now the situation is similar: z0 = stay here; z1 = go back to the q0 state.
This machine can be coded as follows:
MooreAutomaton moore = new MooreAutomaton(new MooreState[] {
new MooreState {
Table = new int[] {
0,
1,
},
Output = 0
},
new MooreState {
Table = new int[] {
1,
0,
},
Output = 1
}
});
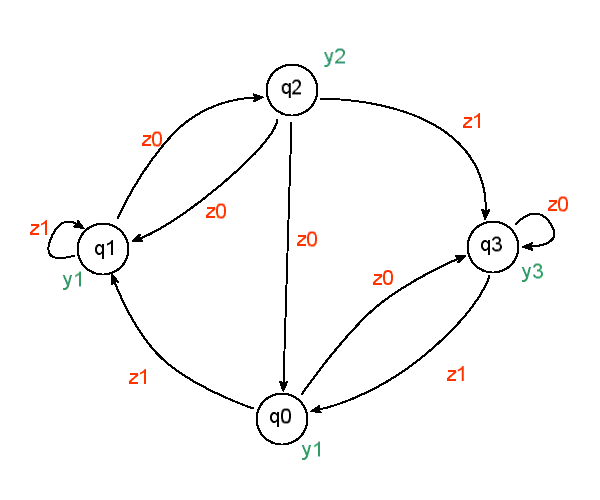
Example 2

The automaton above detects words in a string assuming that they can be separated by white spaces only. If any other character was encountered, the machine is supposed to enter a sink state. State Q is a sink state if and only if there are no transitions leading from Q to another state. Again, we assume that the initial state is q0.
Sending a string "abc de #fg" would give an output 1110110222. Note that the machine gives an output when entering a state. This machine can be easily implemented with an AsciiTableGenerator class:
const int sNothing = 0;
const int sWord = 1;
const int sError = 2;
MooreAutomaton moore = new MooreAutomaton(new MooreState[] {
new MooreState {
Table = new MooreAsciiTableGenerator {
EmptyTransition = sError,
Expressions = {
{ @"\s", sNothing },
{ @"\w", sWord }
}
}.GenerateTable(),
Output = 0
},
new MooreState {
Table = new MooreAsciiTableGenerator {
EmptyTransition = sError,
Expressions = {
{ @"\s", sNothing },
{ @"\w", sWord }
}
}.GenerateTable(),
Output = 1
},
new MooreState {
Table = new MooreAsciiTableGenerator {
EmptyTransition = sError
}.GenerateTable(),
Output = 2
}
});
The AsciiTableGenerator generates a table of 128 integers (ASCII numbers for printable characters). The regular expressions will be evaluated just once when a table is created, so the index of an character is equal to its ASCII value. This solution gives us an O(1) complexity of finding the next state.
If you wish to support all the UNICODE characters, you may want to use a ParsingAutomaton:
ParsingAutomaton parser = new ParsingAutomaton(new ParsingState[] {
new ParsingState {
EmptyTransition = sError,
Expressions = {
{ @"\s", sNothing },
{ @"\w", sWord }
},
Output = 0
},
new ParsingState {
EmptyTransition = sError,
Expressions = {
{ @"\s", sNothing },
{ @"\w", sWord }
},
Output = 1
},
new ParsingState {
EmptyTransition = sError,
Output = 2
}
});
The declaration is similar to the previous one but it evaluates Regex at run-time. Both machines can be executed using the following code:
for (int i = 0; i < inputString.Length; i++)
Console.Write(automaton.Send(inputString[i]));
BTW using a fixed statement instead of inputString[i] is generally recommended.
Example 3 : The INI File Parser
If you are looking for a good INI file parser, then navigate to my article "INI files". Now I'm going to discuss a simple INI file parser which is built of a Moore machine.
First of all, there is another useful visual representation of a Moore machine. Let's examine a structure of an INI file, shall we?
[SectionName]
Key=Value
I can see seven possible states here:
<sub>0</sub>[<sub>1</sub>SectionName<sub>2</sub>]<sub>3</sub>
<sub>0</sub>Key<sub>4</sub>=<sub>5</sub>Value<sub>6</sub>
Now we have to analyze the expression above and decide when a parser should move from one state to another. The important stage of creating an FSA is to test it. A complete solution is included in a test project.
Generating a Super-fast Moore Code
Every Moore FSA can be converted to a program similar to this:
fixed (int* _q = Q) {
int* q = _q;
int y_i = 0;
int[] Y_old;
fixed (int* _r = R) {
fixed (int* _z = Z) {
for (int* z = _z; *q >= 0 && z - _z < Z_len; z++, y_i++) {
int nextq = *(q + *z);
Y[y_i] = *(_r + nextq);
q = _q + stateLen * nextq;
if (y_i >= buferLen - 1) {
Y_old = Y;
Y = new int[buferLen *= 2];
Array.Copy(Y_old, Y, Y_old.Length);
}
}
}
}
Y_old = Y;
Y = new int[y_i];
Array.Copy(Y_old, Y, Y.Length);
}
return Y;
The method FastRun(int[] input) does a quick execution and returns the output as an int[] table. Internally, it generates these Q and R tables and runs the above algorithm. It is quite fast and makes Moore automata programming a considerable solution for performance-critical problems. More documentation can be found around the MooreTables structure.
Useful Wrappers for FSA
Each XxxAutomaton class derives from the FiniteStateAutomaton abstract. It provides a set of basic features and can be used as a bridge between the machine core (e.g. a MooreAutomaton or a MealyAutomaton) and a wrapper class.
Mapped & Match Automata
As you probably noticed, both input and output of a MooreAutomaton are integers. In some cases it is sufficient, but usually we need to send an input of type TInput and receive an output of a type TOutput.
This functionality is provided by the MappedAutomaton and MatchAutomaton classes. For example, we can map the output of an FSA from example 2.
OutputMappedAutomaton<string> mapped = new OutputMappedAutomaton<string>(moore) {
OutputMap = {
{0, " SPACE "},
{1, " WORD "},
{2, " ERROR "},
}
};
mapped.Reset();
for (int i = 0; i < length; i++)
Console.Write(mapped.SendAndMap(s[i]));
The output:
WORD WORD WORD SPACE WORD WORD SPACE ERROR ERROR ERROR
A matching (any idea for a better name?) automaton uses a Converter<TInput, TOutput> delegate to map the external input to internal input and the internal output to external output.
MatchAutomaton<byte, string> mapped = new MatchAutomaton<byte, string>(moore) {
OutputMatch = output => string.Format(" q{0} ", output),
InputMatch = input => (int)input
};
The EventedAutomaton
The evented automaton is extremely useful since it memorizes its recent history and fires events which notify about any change.
EventedAutomaton evented = new EventedAutomaton(moore);
evented.OutputChanged += delegate (object sender, FsaEventArgs e) {
if (e.PreviousOutput == 1) {
StringBuilder build = new StringBuilder();
foreach (int c in e.Automaton.OutputInput) {
build.Append((char) c);
}
Console.WriteLine("Word: {0}", build);
}
};
evented.StateChanged += delegate(object sender, FsaEventArgs e) {
Console.WriteLine("Transition: q{0} -> q{1}", e.State, e.CurrentState);
};
The output:
Transition: q0 -> q1
Word: abc
Transition: q1 -> q0
Transition: q0 -> q1
Word: de
Transition: q1 -> q0
Transition: q0 -> q2
Asynchronous Execution
The FiniteStateAutomaton abstract class provides a few nice features. For example, it supports an asynchronous execution of an FSA.
A sample from the IniFile.cs file:
void OpenAsync(Stream stream)
{
Pipe outputPipe = new Pipe();
IAsyncResult asyncResult = mooreAutomaton.RunAsync(new RunParameters {
Input = stream,
Output = outputPipe
});
However we cannot blame the RunAsync method itself (it is a very simple thing), the code in the IniFile.cs is very slow. A better solution for the thread synchronization problem must be found. Feel free to leave comments and suggestions in the message board below.
Points of Interest
About the Mealy FSA
The difference between Moore and Mealy FSA is a place where the output symbols are. In Moore machines, they were stored as part of a state definition. On the other hand, the output in Mealy machines is assigned to transitions. This approach might greatly reduce a number of states and improve performance but each transition consumes twice as much memory as before. Example 2 can be defined as a Mealy machine below:

MealyAutomaton mealy = new MealyAutomaton(new MealyState[] {
new MealyState {
Table = new MealyAsciiTableGenerator {
EmptyTransition = new MealySymbol { Output = 2, State = 1 },
Expressions = {
{ @"\s", new MealySymbol { Output = 0, State = 0 } },
{ @"\w", new MealySymbol { Output = 1, State = 0 } }
}
}.GenerateTable()
},
new MealyState {
Table = new MealyAsciiTableGenerator {
EmptyTransition = new MealySymbol { Output = 2, State = 1 }
}.GenerateTable()
}
}
);
We can also use a ToMealy conversion method which does all the optimization in O(n3):
MealyAutomaton mealy = moore.ToMealy();
Note about the MealyAsciiTableGenerator class: No special implementation is needed here. The definition of the MealyAsciiTableGenerator class is as below:
public class MealyAsciiTableGenerator : AsciiTableGenerator<MealySymbol>
{
}
The output is obviously the same: 1110110222.
Performance Comparison
A simple test brought predictable results (Pentium Quad 2.4, Vista Business):
Generate: 00:00:03.0150000 // 1000 keys and 1000 values
Save to a file: 00:00:00.6060000
Parsing
Classic: 00:00:01.9270000 (100%) // the IniFileLight from my another article
Mealy automaton: 00:00:00.8690000 (45,1%) // fewer transitions
Moore automaton: 00:00:02.3850000 (123,77%)// fairly comparable with classic parsing
Parsing automaton: 00:00:06.6780000 (346,55%)// regex at run-time
Asynchronous Moore automaton: 00:00:09.2800000 (481,58%) // need to be improved
Fast Moore: 00:00:00.8860000 (45,98%)// ASCII-only, but hey not only for parsing
A Bonus Content
I give you some bonus classes.
- The
Pipe is a multithreading-oriented memory stream. It is supposed to be read and written from two or more threads. Both Write and Read methods block the current thread until it is possible to obtain a requested amount of data or until there is enough space to write. It uses a fixed-sized buffer which can be defined in a constructor. Closing the stream disallows writing to it but data can still be read from the buffer. This prevents from a lock-forever state when a source of data finishes its job and the reader has its own buffer (for example a StreamReader). There is also a time-out support. - The
RestictedList<T> is a class which derives from the List<T>. It gives a possibility to set criteria which items must meet to be added to a list. If a user tried to add an item which didn't meet the criteria, an exception would be thrown. The criteria are defined by a Predicate<T> delegate. RestictedDictionary<TKey, TValue> - analogous to the RestrictedList<T> class.
Extending FSA Functionality
You need to implement 3 methods to make an extension to a standard FSA machine.
public class MyAutomaton : FiniteStateAutomaton
{
private readonly FiniteStateAutomaton fsa;
public MyAutomaton(FiniteStateAutomaton fsa)
{
this.fsa = fsa;
}
public override void Reset()
{
fsa.Reset();
}
public override int Send(int input)
{
int output = fsa.Send(input);
return output;
}
public override FiniteStateAutomaton ShallowCopy()
{
MyAutomaton copy = new MyAutomaton(fsa.ShallowCopy());
return copy;
}
}
Summary
In this article, I tried to prove that FSA systems are not as obsolete technology as they are considered. I am sure that there are cases where FSA could be used even as a design pattern. With a well-designed automaton, a fast and robust system can be created. Since every automaton may be presented in a graph form, a myth about obscurity of FSA is false. Even if a graph was lost, with a little effort we could develop a software which generates such graphs or just take a sheet of paper and make a damn artwork. Because of their generic nature, bugs like not investigated cases can be discovered quickly, even without a human contribution.
I hope that I managed to refresh the FSA technique well enough to bring it back to developers. Happy graphing!
TODOs
- Improve performance of asynchronous operations
- Find a better name for the
MatchAutomaton - As usual, track down bugs (so far so good)
History
- 31st January, 2009: First version posted
- 3rd February, 2009: Article updated
