Table of Contents
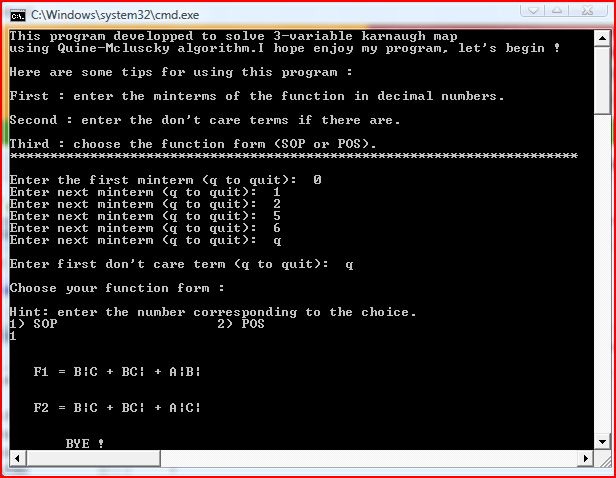
This program provides a general code in C language (you can call it pseudo code) that can be implemented in other languages to solve the 3-var Karnaugh map.
The program uses the Quine-McClusky algorithm and Petrick's method as they are easy to implement in programming.
Here are some tips to use this program:
- Enter the minterms in decimal numbers, when you finish, enter 'q' character to quit.
- Enter the Don't care terms (if they exist), when you finish, enter 'q' character to quit.
- Choose the function form (SOP or POS).
I'll start first with the algorithm to make the code easy to understand.
The Quine - McClusky algorithm was developed to implement karnaugh maps that are too important in digital design or simplifying the boolean functions. The algorithm consists of some steps we must handle to make our project or code work perfectly without any errors.
Gather all minterms & don't care terms (if there are any) and convert them to binary form, then sort them in groups and list them in a list (call it List 1).
Example: If we have these terms (0,1,2,3,4,7,6), then the groups should be like this:
- group 0 contains the binary [000]
- group 1 contains the binaries [001 (0 in decimal) , 010 (2 in decimal), 100 (4 in decimal)]
- group 2 contains the binaries [011 (3 in decimal), 110 (6 in decimal)]
- group 3, final group, contains the binary [111 (7 in decimal)]
We can see in these groups that they are sorted according to the number of ones in each binary number.
Compare group 1 with group 2 & group 2 with group 3 & group 3 with group 4, the comparison is achieved by comparing each term in the first group with all terms in the next group.The comparison concept is that if two terms have only 1 different bit, then this bit must be replaced with (-) like: (000 , 001) ==> (00-).
After the comparison is done in (List 1), move to List 2 and do the same comparison, but we will find a new element, the dash (-) that we must handle it in the comparison. When we compare two dashed terms, the comparison is legal only if the dash position is the same in the two terms, otherwise we can't compare those terms like: (00- , 01-) ==> (0--), but (00- , 0-1) is illegal.
If two terms compared successfully, a check character is put next to the compared terms (say the check chr is 't'), if not, I mean that the two terms have more different bits or the dash position is not the same in the two terms, then a check character must be put next to the uncompared terms (say check chr is '*') to indicate something we will discuss in step 3.
Note: If two terms can't be compared say a term in group 2 & term in group 3, if the term that is in group 3 can be compared later with a term in group 4, then the ('*') indicator must be replaced or overwritten by ('t') indicator.
| List 1 | List 2 | List 3 |
| group 0 | 000t | 00-t | 0--* |
| | 0-0t | --0* |
| | -00t | |
| group 1 | 001t | 0-1t | -1-* |
| 010t | 01-t | |
| 100t | -10t | |
| | 1-0t | |
| group 2 | 011t | -11t | |
| 110t | 11-t | |
group 3
| 111t | | |
Determine the prime implicants (if they are found in any list above).
Note: The prime implicants are terms that can't be compared any more and indicated with '*', like: (0-- , --0 , -1-).
Form the coverage table to determine the essential prime implicants. To form this table, we will put the minterms horizontally & the prime implicants vertically, then we should determine which terms a prime implicant cover like (0--) covers 0,1,2,3. and put an indicator (say 'X') in the cells corresponding to the row of prime implicant and its terms.
| 0
| 1
| 2
| 3
| 4
| 6
| 7
|
0-- (0,1,2,3)
| x
| x
| x
| x
| | | |
| --0 (0,2,4,6) | x
|
| x
|
| x
| x
| |
| -1- (2,3,6,7) |
|
| x
| x
|
| x
| x
|
Now after we finished the table, we can determine the essential prime implicants by dominating the row and column of a term that has only 'X' in his column, like : (1 , 4 , 7). By dominating these rows, we can say that the prime implicants corresponding to these rows became essential prime implicants.
Finding the Simplified function. As we know, our example gives us these terms to simplify (0, 1, 2, 3, 4, 6, 7). Those terms without simplifying should form this function:
F = A'B'C' + A'B'C + A'BC' + A'BC + AB'C' + ABC' + ABC
where, A, B, C are variables and A', B', C' are their compliment variables & their compliments are called literals representing the binary form of the terms.
After simplifying, the function looks like this:
F = A' + C' + B
There is another step left before (step 5) that handles the prime implicants left in the table using the Petrick's method. We will discuss it with some conditions we may meet later in another example.
- A group is missing, what happens if a group like group 2 is missing?
In this situation, group 0 & group 1 can be compared but group 1 can't be compared any more because group 2 is missing and therefore group 3 is left as it is and the term in group 3 considered as prime implicant.
- Repeated terms, while we comparing terms with others, repeated terms we may meet in the results.
Example, in the previous example at list 2, the terms (00- , 01-) can be compared and the result will be the term (0--).The terms (0-0 , 0-1) can be compared too and the result will be (0--), so the term (0--) is repeated and we can't put it twice in list 3.
- If we entered all minterms (0, 1, 2, 3, 4, 5, 6, 7), the resulted function can be considered directly as the value 1 (F = 1) without using any steps mentioned before.
- The don't care terms, don't care terms need special handling in Quine-McClusky algorithm, so if a problem or an example has thus terms, we will execute the steps 1,2,3 considering thus terms are minterms which we handled in the previous example but in step 4 thus terms must not be added in the coverage table.
Example: If we have this problem, F = m(0,1,2,6) + d(4,5), all terms, minterms & don't cares are handled normally with steps 1,2,3 but terms (4, 5) must not be included in the coverage table.
To implement step 1, we should take the inputs (minterms & don't caresa) from user in numbers, storing minterms in array & don't care in another array, then converting these numbers to its binary equivalent. There are many approaches to convert decimal numbers to binary numbers, here is a common technique implemented in a function.
char *ConvertToBinary(int num, char *bin)
{
int i;
int mask = 1;
int size = BINSIZE;
for (i = size - 1; i >= 0; i--, num >>= 1)
bin[i] = (mask & num) + '0';
bin[size] = '\0';
return bin;
}
When the inputs are all converted to binary numbers, we will sort it in groups using data structure that contains four 2-D arrays and dividing these groups to three lists using array of structures.
typedef struct q_mc {
char ar0[SIZE][ROWSIZE];
char ar1[SIZE][ROWSIZE];
char ar2[SIZE][ROWSIZE];
char ar3[SIZE][ROWSIZE];
}Q_MC;
Q_MC ar[NUMLIST] = {""};
After storing the data that the user entered in the structure of first element (list1) in the array <code>ar, we should now compare the groups (data structures we just created) by using this function:
int CompareTerms(const char *ar1, const char *ar2, int size)
{
int i;
int count = 0;
int temp;
for (i = 0; i < size; i++)
{
if (ar1[i] != ar2[i])
{
temp = i;
count++;
}
else
continue;
}
return (count == 1) ? temp : -1;
}
The previous function takes two strings 'ar1' & 'ar2', these strings represent the binary form of the terms like (01- , 11-).After the function takes its arguments, the for loop checks on every character in the two strings and if a character is different in a one string from another in the second string, the function returns the position of this character, else return (-1).
After completing the comparison, the check characters (t , *) should be attached next to the compared terms. We can do this by using the following piece of code:
if (bit_pos != -1)
{
for (j = 0; j < BINSIZE; j++)
{
if (j == bit_pos)
ar[1].ar0[_rows0][j] = '-';
else
ar[1].ar0[_rows0][j] = ar[0].ar1[index][j];
}
ar[0].ar0[0][BINSIZE] = 't';
ar[0].ar0[0][BINSIZE+CHKCHAR] = '\0';
ar[0].ar1[index][BINSIZE] = 't';
ar[0].ar1[index][BINSIZE+CHKCHAR] = '\0';
ar[1].ar0[_rows0][BINSIZE+CHKCHAR] = '\0';
_rows0++;
}
else
{
if (ar[0].ar0[0][BINSIZE] != 't')
ar[0].ar0[0][BINSIZE] = '*';
ar[0].ar0[0][BINSIZE+CHKCHAR] = '\0';
if (ar[0].ar1[index][BINSIZE] != 't')
ar[0].ar1[index][BINSIZE] = '*';
ar[0].ar1[index][BINSIZE+CHKCHAR] = '\0';
}
Let's start with the condition: if (bit_pos!= -1), bit_pos variable stores the returned value of the CompareTerms function. The for loop keeps track of the binary form of the term till j variable reaches the different bit's position, if so the bit replaced with dash '-', otherwise, do nothing, then put the new binary form in the new list.
After the new binary form was created, we will attach the character 't' to the two compared terms and a '*' to the uncompared terms, but if the terms are already attached with 't' character, it shouldn't replaced with '*' if they can't be compared with the other terms.
Hint:
ar[0] refers to list 1.
ar[1] refers to list 2.
ar[0].ar0 refers to group 0 in list 1.
ar[0].ar1 refers to group 1 in list 1.
ar[1].ar0 refers to group 0 in list 2.
Determining the prime implicants. When we put the check characters, now determining which term is prime implicant or not became too easy in programming, the only thing we will do is using the "strchr" function to find if the '*' indicator is found in a string or not, remember '*' referes to prime implicants terms. As an example, I'll illustrate how we can catch the prime implicants at group 0 in list 2 with the following code:
for (index = 0; index < _rows0; index++)
{
if (strchr(ar[1].ar0[index], '*') != NULL)
{
for (j = 0; j < BINSIZE; j++)
prime_imp[k][j] = ar[1].ar0[index][j];
prime_imp[k++][BINSIZE] = '\0';
}
}
_rows0 is the number of terms at group 0 in list2, if the '*' character found in any term in the group, it will be copied to a new array holding the prime implicants.
Finding the essential prime implicants. This part determines the essential prime implicant that will form the boolean function we need.
The dashes in each prime implicant are converted first to the binary states, then the binaries converted to the decimal numbers. As an example, if the prime implicant has one dash, so we got only two states (0 or 1), if it has two dashes, we got four states (00 or 01 or 10 or 11).
After we finished this replacement, we will convert all the binaries resulted to the terms that has been covered by them.
Example: The prime implicant (0--) is manipulated as follows:
(-1-) = replace dashes => (010 , 011 , 110 , 111) When we get these binaries, now we can compare each one of them to the binary form of the inputs to determine the term identical to the state of prime implicant.
If the binaries of an input & a state of the prime implicant, the index of the input or the input itself stored in array.This code can implement the comparison part:
for ( m = 0; m < n; m++)
if (strcmp(store_inputs[m],prime_imp_bin) == 0)
store_index[l++] = m;
Where, n is the number of inputs.
store_inputs is a (2-D) array holds the binaries of the inputs. prime_imp_bin array holds a state of the prime implicant. store_index array stores the index of each input which is identical only to the states of prime implicant.
After storing the indices of our inputs which are identical to states of prime implicants, we will sort these indices in increasing order to remove the repeated indices easily.
Why we removed the repeated indices of minterms in the coverage table?
Answer: To pick up the rest of minterms' indices which are unreapted.The minterms referred by the unrepeated indices guide us to the essential prime implicants that will form our function.
Hint: The unrepeated minterms are terms that have only one 'X' (bolded one) marker that was indicated in the coverage table.
And here is the code that implements the sort and remove part:
qsort(store_index, l, sizeof(int), mycomp);
j = 0;
for (m = 0; m < l; m++)
{
if (store_index[m] == store_index[m+1])
continue;
else if (store_index[m] != store_index[m+1] && store_index[m] == store_index[m-1])
continue;
else
store_index2[j++] = store_index[m];
}
The qsort function is used to sort alphapetic & numeric characters, as we see, it takes an array that holds the data we want to sort, length of this array, size of data type held by the array and the mycomp function that is considered as a fuel to the function without mycomp function, qsort will do nothing.
If we have two numbers say (n1,n2), mycomp function returns -1 if n1 < n2 , 0 if n1 = n2 and the value 1 if n1 > n2.
Now after we got the minterms that refer to prime implicants which are supposed to be essential prime implicants, we will use these terms which their indices stored in store_index2 array to get our essential primes.
We can use the following block of code to get our target:
for ( m = 0; m < unrepeated_terms; m++)
{
if (strcmp(store_inputs[store_index2[m]],prime_imp_bin) == 0)
{
prime_imp[index][BINSIZE] = '*';
prime_imp[index][BINSIZE+CHKCHAR] = '\0';
strncpy(ess_pri_imp[p++], prime_imp[index], BINSIZE);
}
}
The unreapted_terms variable is the number of unrepeated terms (that have only one X in its column), the strcmp function compares between each input (binary form) and each state of a prime implicant, at any condition they are equal, the prime implicant itself is not a state of it copied to the ess_pri_imp array. See the complete code of finding the essential prime implicants part in 3_var.cpp file starting with line 473 to line 730.
Our function has two forms, SOP and POS. SOP means Sum Of Products and POS means Product of Sum.
To form the SOP function, first convert each essential prime implicant to alphapetic form.
Example: If we have these essential implicants (0-1, 111, --0), the alphapetic form of these terms should be like that:
0-1 ===> A|C
111 ===> ABC
--0 ===> C|
In the previous example, we used the letters A,B,C. Actually, we can use any letters like X,Y,Z. At any SOP form the zero bit takes the complement of the letter (letter + bar) and because we don't have bar symbol, I used this symbol '|' to represent the complement of a letter.
Second: Put after each term a '+' operator.
Example, the function that represents the previous terms is " F = A|C + ABC + C| ".
Let's see the code that can implement the SOP form:
printf("\n\n F = ");
for (index2 = 0; index2 < unrepeated_terms2; index2++)
{
for (j = 0; j < BINSIZE; j++)
{
switch (j)
{
case 0:
if (ess_pri_imp2[index2][j] == '0')
printf("A|");
else if (ess_pri_imp2[index2][j] == '1')
putchar('A');
break;
case 1:
if (ess_pri_imp2[index2][j] == '0')
printf("B|");
else if (ess_pri_imp2[index2][j] == '1')
putchar('B');
break;
case 2:
if (ess_pri_imp2[index2][j] == '0')
printf("C|");
else if (ess_pri_imp2[index2][j] == '1')
putchar('C');
break;
}
}
if (index2 % unrepeated_terms2 == index2 && (unrepeated_terms2 - index2) > 1)
{
putchar(' ');putchar('+');putchar(' ');
}
}
The outer loop checks the content of ess_pri_imp2 array that contains the essential prime implicants. The variable unrepeated_terms2 is the number of essential prime implicants we have.
The inner loop checks the bits of each essential implicant. Then I used a switch to divide each implicant to positions (0,1,2). Each position can take a letter or its complement according to the state of bit in that implicant.
The final if condition in the code controls adding '+' operators after each term except the final term in the function.
Forming the POS function, we use the same procedure as SOP but in POS we convert the zero bit to the complement of a letter and the one bit takes the normal letter and we put after each letter that represent a bit a '+' operator to separate the literals (letters that represent the bits), then we add each term in parenthesis to make each term looks like a sum term and the function looks like a product of sum.
- http://en.wikipedia.org/wiki/Quine%E2%80%93McCluskey_algorithm
- http://en.wikipedia.org/wiki/Petrick%27s_Method
- Digital Design Fundamentals, 2nd Ed [Kenneth J. Breeding]
- Digital Fundamentals 9e [Floyd]
Help
My friend always says "Nobody is perfect, but a team can be", so I hope someone can complete this code to cover more than 3 variables.
