Introduction
This article shows an algorithm for the classification of a set of points into groups (clusters) according to their relative positions by putting into work some of the .NET features like Generic Collections, LINQ, Partial Classes, and Lambda Expressions.
Background
Clusterization algorithms are a well studied subject, and articles about it are easily found on the Internet.
At the core of each algorithm, there is always a loop, or series of loops, to traverse the set of points and classify them into groups (clusters) according to a certain criteria. In this article, I show how, by taking advantage of .NET collection classes, LINQ, and Lambda Expressions, an algorithm can be simplified.
First, some definitions to establish a common parlance:
- The algorithm's entry data will be a set of points {P}, let N be the total number of points in {P}; and a number (distance) D.
- Two points of {P} are said to be directly connected if their relative (Euclidian) distance is less or equal than D.
- Two points of {P} are said to be indirectly connected if a path of directly connected points can be established between them.
- A cluster is a subset of points of {P} that are (directly or indirectly) connected among them.
- A point can only belong to one cluster.
- If a point is not directly connected to any other point, then it forms all by itself one cluster. That cluster contains only one point.
- The result of the algorithm will be a set clusters {C}. This set describes how the points in {P} are grouped when following the above rules.
- Each individual member of {C} lists a subset of {P}.
Sorry, the last two sentences sound more complicated than what in reality the problem is. OOP clarifies these matters in the code.
Using the code
The class Point describes a point of the above mentioned set {P}. {P} itself is represented in code by a .NET generic collection l_ListPoints. The class Cluster has a property describing the points inside the cluster of type List<Point>. {C} is represented in code by l_ListClusters. The actual data for the points was generated using C#'s not-so-random generator and set into a .NET partial class BasicLibrary.AuxListPoint (spread in files AuxListPoint.cs and points.cs). The bottom line is the positions of the points are hardcoded for the sake of the example.
Figure 1 displays the core of the algorithm:
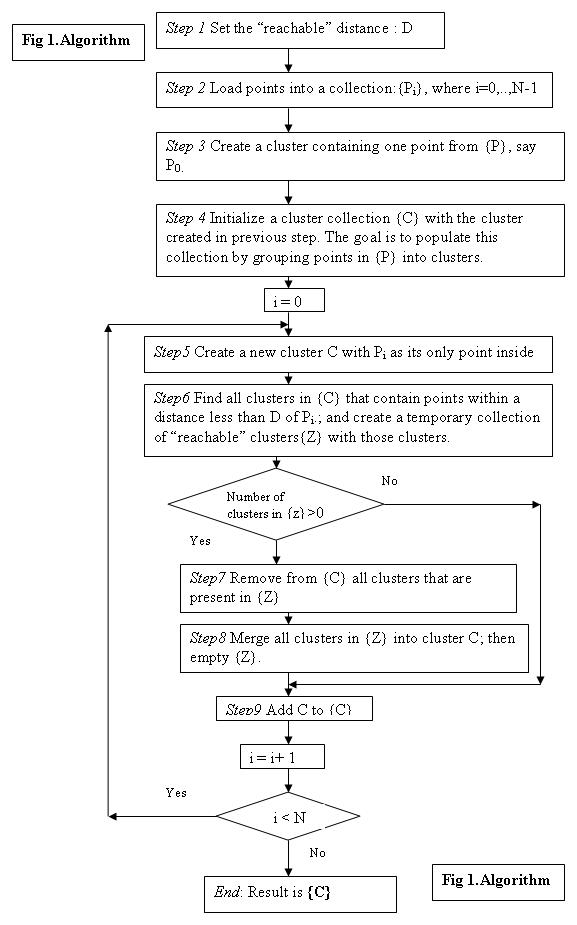
The simplification provided by using the .NET features can be seen in the coding of steps 6, 7, and 8 (see Fig 1). If we weren't using .NET, then we would have to code steps 6, 7, and 8 into elaborated sub-algorithms to handle collections.
In code, the implementation of those steps looks like:
#region Main Loop
List<Cluster> l_ListAttainableClusters;
Cluster l_c;
foreach (BasicLibrary.Point p in l_ListPoints)
{
l_ListAttainableClusters = new List<Cluster>();
l_ListAttainableClusters = l_ListClusters.FindAll(x => x.IsPointReachable(p));
l_ListClusters.RemoveAll(x => x.IsPointReachable(p));
l_c = new Cluster(l_Dist, p);
if (l_ListAttainableClusters.Count > 0)
l_c.AnnexCluster(l_ListAttainableClusters.Aggregate((c, x) =>
c = Cluster.MergeClusters(x, c)));
l_ListClusters.Add(l_c);
l_ListAttainableClusters = null;
l_c = null;
}
#endregion
Points of interest
It is worth mentioning that real life clusterization applications often deal with a huge number of points, and the performance of the algorithm is of the essence in those cases. The algorithm presented here hasn't been tested for a number of points greater than fifty thousands points; its performance for greater sets could be an issue.
There is a WPF app and a console app in the solution (see source code). Both use the same algorithm. The WPF project comes with a graphic display of the clusterization that is colorful but has yet to prove to be meaningful (Fig. 2 and Fig. 3 are examples of running the WPF app with two different D values). In the graphics, I used a helper class described in http://www.codeproject.com/KB/graphics/WpfCoordExample.aspx.


