Introduction
There are many available articles on The Code Project discussing about neural network concept and implementation. But when I wanted to find out how to implement Nguyen-Widrow initialization algorithm, I could not find one. So I searched through the internet, read some scientific papers and books and finally tried to implement those things I read into an applicable algorithm in C++. For us, as students, there are big gaps between things we learn in class and how to implement them into real world applications. By putting all things that I managed to learn into a single C++ class (CNeuralNetwork) and share them, I hope I can help others who encounter the same problem. The main neural network code here is based on Daniel Admassu work. Things I managed to implement in this class are:
- Weight initialization algorithm (some ordinary methods and Nguyen-Widrow method)
- Momentum learning
- Adaptive learning
Those three concepts will make the neural network we created able to learn faster (with less iterations). Although those are still minor thingies, I think it is a good idea to share them here.
Background
You might need a basic understanding of neural network theory. Since I am using back propagation method (the simple one), I am sure you can find a lot of tutorials about it.
Concepts
Feed-forward
Here we are using multilayer percepteron (MLP) neural network architecture. MLP consists of several layers, interconnected through weighted connections. MLP has at least three layers, they are input layer, hidden layer, and output layer. We can have several hidden layers. In each neuron, we assign an activation function which will be triggered by weighted input signal. The idea is: we want to find the appropriate value for all weights so that one set of input that we give will results in one set of output as we desire.
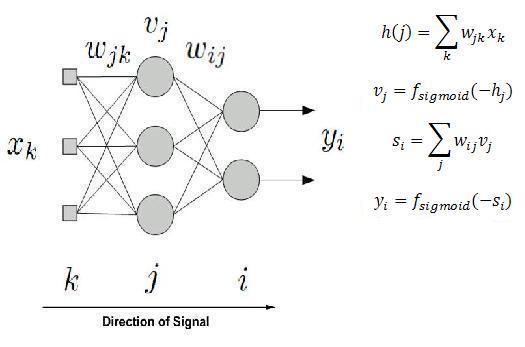
Here, for CNeuralNetwork, I use bipolar logistic function as the activation function in hidden and output layer. While in input layer, I use unity function. Choosing an appropriate activation function can also contribute to a much faster learning. Theoretically, sigmoid function with less saturation speed will give a better result.

In CNeuralNetwork, I only provide bipolar logistic function. But you can manipulate its slope (s) and see how it affects the learning speed. A larger slope will make weight values move faster to saturation region (faster convergence), while smaller slope will make weight values move slower but it allows a refined weight adjustment.

Back-propagation
In feed-forward process, the network will calculate the output based on the given input. Next, it will compare this calculated output to the desired output to calculate the error. The next mission is to minimize this error. What method we choose for minimizing this error will also determine the learning speed. Gradient descent method is the most common for minimizing this error. Finally, it will update the weight value as the following:

where:

Besides this gradient descent method, there are several other methods that will guarantee a faster learning speed. They are conjugate gradient method, quasi-Newton method, Levenberg-Marquardt method, and so on. But for me, those methods are too complicated. So, instead of using those methods, we can make the learning process much faster by adding momentum term or by using adaptive learning rate.
Adding Momentum Term
In momentum learning, weight update at time (t+1) contains momentum of the previous learning. So we need to keep the previous value of error and output.

The equation above can be implemented as the following. Variable a is the momentum value. The value should be greater than zero and smaller than one.
void CNeuralNetwork::calculate_weights()
{
for(unsigned int i=1;i<m_layer_num;i++){
for(unsigned int j=0;j<m_neuron_num[i];j++){
for(unsigned int k=0;k<m_neuron_num[i-1];k++){
float delta = m_learning_rate * m_error[i][j] * m_node_output[i-1][k];
float delta_prev = m_learning_rate * m_error_prev[i][j]
* m_node_output_prev[i-1][k];
m_weight[i][j][k] = (float) m_weight[i][j][k] + delta +
m_momentum * delta_prev;
}
}
}
}
Adaptive Learning
For adaptive learning, the idea is to change the learning rate automatically based on current error and previous error. There are many methods to perform this idea. Here is the easiest that I can find.

The idea is to observe the last two errors and adjust the learning rate in the direction that would have reduced the second error. Both variable E and Ei are the current and previous error. Parameter A is a parameter that will determine how rapidly the learning rate is adjusted. Parameter A should be less than one and greater than zero. You can also try another method by multiplying the current learning rate with a factor greater than one if current error is smaller than previous error. And if current error is bigger than previous error, you can multiply it with a factor less than one. In Martin Hagan book, it is also suggested that you discard the changes if the error is increasing. This will lead into a better result.You can find adaptive learning routine in function ann_train_network_from_file where learning rate update is performed once per epoch.
int CNeuralNetwork::ann_train_network_from_file
(char *file_name, int max_epoch, float max_error, int parsing_direction)
{
int epoch = 0;
string line;
ifstream file (file_name);
m_average_error = 0.0F;
if (file.is_open()){
for (epoch = 0; epoch <= max_epoch; epoch++){
int training_data_num = 0;
float error = 0.0F;
while (! file.eof() ){
getline(file, line);
if (line.empty()) break;
parse_data(line, parsing_direction);
calculate_outputs();
calculate_errors();
calculate_weights();
error = error + get_average_error();
training_data_num ++;
}
file.clear(); file.seekg(0, ios::beg);
float error_prev = m_average_error;
m_average_error = error/training_data_num;
if (m_average_error <= max_error)
break;
m_learning_rate = m_learning_rate*
(m_lr_factor*m_average_error*error_prev + 1);
}
}
file.close();
return epoch; }
Weight Initialization Algorithm
From several papers I read, it is known that the particular initialization values give influences to the speed of convergence. There are several methods available for this purpose. The most common is by initializing the weights at random with uniform distribution inside the interval of a certain small range of number. In CNeuralnetwork, I call this method HARD_RANDOM because I cannot find the existing name for this method. Another better method is by bounding the range as expressed in the equation below. In CNeuralNetwork, I call this method with just RANDOM.

Widely known as a very good weight initialization method is the Nguyen-Widrow method. In CNeuralNetwork, I call this method as NGUYEN. Nguyen-Widrow weight initialization algorithm can be expressed as the following steps:

As stated in the algorithm as written above, first, we assign random number of -1 to 1 to all hidden nodes. Next, we calculate the norm of these random numbers that we have generated by calling function get_norm_of_weight. Now we have all the necessary data and we can proceed to the available formula. All the weight initialization routines are located in function initialize_weights.
void CNeuralNetwork::initialize_weights()
{
if (m_method == HARD_RANDOM){
for(unsigned int i=1;i<m_layer_num;i++)
for(unsigned int j=0;j<m_neuron_num[i];j++)
for(unsigned int k=0;k<m_neuron_num[i-1];k+
m_weight[i][j][k]=rand_float_range(-m_init_val, m_init_val);
}
else if (m_method == RANDOM){
float range = sqrt(m_learning_rate / m_neuron_num[0]);
for(unsigned int i=1;i<m_layer_num;i++)
for(unsigned int j=0;j<m_neuron_num[i];j++)
for(unsigned int k=0;k<m_neuron_num[i-1];k++)
m_weight[i][j][k]=rand_float_range(-range, range);
}
else if (m_method == NGUYEN){
for(unsigned int i=1;i<m_layer_num;i++)
for(unsigned int j=0;j<m_neuron_num[i];j++)
for(unsigned int k=0;k<m_neuron_num[i-1];k++)
m_weight[i][j][k]=rand_float_range(-1, 1);
for(unsigned int i=1;i<m_layer_num;i++){
float beta = 0.7 * pow((float) m_neuron_num[i], (float) 1/m_neuron_num[0]);
for(unsigned int j=0;j<m_neuron_num[i];j++){
for(unsigned int k=0;k<m_neuron_num[i-1];k++)
m_weight[i][j][k]=beta * m_weight[i][j][k] / get_norm_of_weight(i,j);
}
}
}
}
Using The Code
Public methods:
- Create a new neural network.
void ann_create_network(unsigned int input_num, unsigned int output_num,
unsigned int hidden_layer_num, ...);
- Set learning rate value.
void ann_set_learning_rate(float learning_rate = 0);
- Set momentum value.
void ann_set_momentum(float momentum = 0);
- Set learning rate changing factor for adaptive learning feature.
void ann_set_lr_changing_factor(float lr_factor = 0);
- Set slope value for logistic sigmoid activation function.
void ann_set_slope_value(float slope_value = 1);
- Set desired weight initialization method.
void ann_set_weight_init_method(int method = NGUYEN , float range = 0);
- Set current input per neuron in input layer.
void ann_set_input_per_channel(unsigned int input_channel, float input);
- Get last average error in one epoch after a training completes.
float ann_get_average_error();
- Get the output after performing simulation.
float ann_get_output(unsigned int channel);
- Get number of epoch needed to complete training.
float ann_get_epoch_num();
- Train the neural network with train set from a text file. Text file for train set can be a comma separated or white-space separated file. Set the
parsing_direction to become INPUT_FIRST if in that text file input comes first. If output comes first, set the parsing_direction to become OUTPUT_FIRST. Result of the training, such as weight values, number of epochs required, final average MSE in one epoch, etc. will be logged to file result.log.
int ann_train_network_from_file(char *file_name, int max_epoch, float max_error,
int parsing_direction);
- Test the trained neural network with test set from a text file specified in parameter
file_name. The result will be logged to another file specified in parameter log_file.
void ann_test_network_from_file(char *file_name, char *log_file);
- Simulate the neural network based on the current input.
void ann_simulate();
- Delete all previous dynamically created dynamic variables, avoiding memory leakage.
void ann_clear();
The following is the example of how to use CNeuralNetwork. I put this class is in file Neural Network.h and Neural Network.cpp. If you want to use this class, you just need to include these two files in your project.
#include "stdafx.h"
#include "Neural Network.h"
int main()
{
float *result;
CNeuralNetwork nn;
nn.ann_set_learning_rate(0.5);
nn.ann_set_momentum(0);
nn.ann_set_lr_changing_factor(0);
nn.ann_set_slope_value(1);
nn.ann_set_weight_init_method(nn.NGUYEN);
nn.ann_create_network(2,1,1,3);
int epoch = nn.ann_train_network_from_file("input.txt", 500, 0.01, nn.OUTPUT_FIRST);
printf("number of epoch: %i with final error:
%f\n",epoch, nn.ann_get_average_error());
nn.ann_set_input_per_channel(0, 1.0F);
nn.ann_set_input_per_channel(1, 1.0F);
nn.ann_simulate();
printf("%f\n", nn.ann_get_output(0));
nn.ann_set_input_per_channel(0, 0.0F);
nn.ann_set_input_per_channel(1, 0.0F);
nn.ann_simulate();
printf("%f\n", nn.ann_get_output(0));
nn.ann_set_input_per_channel(0, 1.0F);
nn.ann_set_input_per_channel(1, 0.0F);
nn.ann_simulate();
printf("%f\n", nn.ann_get_output(0));
nn.ann_set_input_per_channel(0, 0.0F);
nn.ann_set_input_per_channel(1, 1.0F);
nn.ann_simulate();
printf("%f\n", nn.ann_get_output(0));
nn.ann_clear();
}
Experiment
To see how these ideas work, we will carry out some experiments with classic XOR problem. For this XOR problem, we will create a neural network that consists of 1 hidden layer with 3 neurons. First we will see how effective weight initialization issue is in a neural network. Then we will try to activate momentum learning and adaptive learning feature and see how the learning process gains more speed. Our target is to achieve average mean squared error of one epoch = 0.01. All the experiments are conducted with learning rate = 0.5 and maximum number of epoch is limited to 500 epochs. From the experiment, we can see how the existing methods will speed up the training process more than twice.
- Learning rate changing factor = 0; Momentum = 0; Weight initialization method = HARD_RANDOM with range -0.3 to 0.3.
Target of minimum mean square error is not achieved within 500 epochs.

- Learning rate changing factor = 0; Momentum = 0; Weight initialization method = RANDOM.
Target of minimum mean square error is not achieved within 500 epochs.

- Learning rate changing factor = 0; Momentum = 0; Weight initialization method = NGUYEN.
Target of minimum mean square error is achieved within 262 epochs.

- Learning rate changing factor = 0; Momentum = 0.5; Weight initialization method = NGUYEN.
Target of minimum mean square error is achieved within 172 epochs.

- Learning rate changing factor = 0.5; Momentum = 0; Weight initialization method = NGUYEN.
Target of minimum mean square error is achieved within 172 epochs.

Points of Interest
All the code is implemented in a single class: CNeuralNetwork. In that way, I hope it will be simple and easy enough to understand especially for students seeking more information about neural network implementation in C++. For further work, I still have an intention to learn more and to implement things I learn here with an expectation that it will be useful for others. For your information, I also included an extra training file from UCI database. You can use this file to test your neural network. Since this class is using basic function of C++, it will also run nicely in Linux.
References
- Back Propagation Algorithm, by Wen Yu
- Nguyen, D. and Widrow, B., "Improving The Learning Speed of 2-layer Neural Networks by Choosing Initial Values of The Adaptive Weights", IJCNN, USA, 1990
- Mercedes Fernández-Redondo, Carlos Hernández-Espinosa, "A Comparison among Weight Initialization Methods for Multilayer Feedforward Networks," IJCN, Italy, 2000
- Prasanth Kumar, Intelligent Control Lecture Note, School of Mechanical and Aerospace Engineering, Gyeongsang National University, Republic of Korea
History
- 9th August, 2009: Initial version
