Introduction
The principle of decision is not complex. Start from the root node, compare the feature value stored in node with the corresponding feature value of the test object. Then, turn to left substree or right substree recursively according to the comparison result. Finally, the label of the leaf node is the prediction of the test object.
For example, there is a decision tree below, where the feature set is {hungry, money} and the label set is {go to restaurant, go to buy a hamburger, go to sleep}.
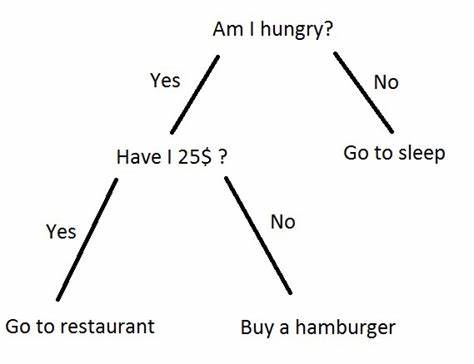
In the decision process, first if I am hungry, turn to the right subtree, which means I will go to sleep. Else turn to the left subtree. Then, check how much money in my wallet. If I have more than 25$, I will go to restaurant. Else, I can only go to buy a hamburger.
Decision Tree Model
Decision Tree model consists of feature selection, generation of decision tree and classify.
Feature Selection
The aim of feature selection is to choose the feature which has the ability of classification for training data to make the learning process more efficient. Feature selection includes two parts, namely, feature selection and feature value selection. The selected tuple (feature, feature value) are applied as the node in the decision tree.
Feature selection is usually based on information gain or information gain ratio. Information gain is defined as the difference between the empirical entropy of set D,  and the conditional entropy under selecting feature A,
and the conditional entropy under selecting feature A, , which is calculated as:
, which is calculated as:

Specifically, when the data set D is divided into two subset by feature A, the information gain is expressed as:

where  is the ratio of the first subset, namely:
is the ratio of the first subset, namely:

The code of calculation of information gain is shown below:
left_set, right_set = self.divideData(data, i, value)
ratio = float(len(left_set)/sample_num)
if ratio == 0.0:
info_gain = init_entropy - (1 - ratio) * self.getEntropy(right_set[:, -1])
elif ratio == 1.0:
info_gain = init_entropy - ratio*self.getEntropy(left_set[:, -1])
else:
info_gain = init_entropy - ratio *
self.getEntropy(left_set[:, -1]) - (1 - ratio) * self.getEntropy(right_set[:, -1])
So far, we have learned how to calculate the information gain. But, how to calculate the empirical entropy? The empirical entropy is the entropy of the labels of the training set, which is given by:

The above equation looks a bit complex but it is very easy to implement. Let's look at the code of it:
def getEntropy(self, labels):
labels_num = len(labels)
label_count = self.uniqueCount(labels)
entropy = 0.0
for j in label_count:
prop = label_count[j]/labels_num
entropy = entropy + (-prop*math.log(prop, 2))
return entropy
Generation of Decision Tree
There are many algorithms to generate decision tree, such as ID3, C4.5. In this article, we take ID3 algorithm as the example to generate the decision tree.
First, let's figure out the split process after feature selection. It is known to us that feature selection is to make the data classifiable. Thus, the split process is to divide the training data according to the selected feature index and its selected value value. Specifically, the split process is that if the index feature value in a sample is larger than value, then add the sample into right subtree and delete the index feature in the sample; else if the index feature value in a sample is smaller than value, then add the sample into left subtree and delete the index feature in the sample. The code of split process is:
def divideData(self, data, index, value):
left_set = []
right_set = []
for temp in data:
if temp[index] >= value:
new_feature = np.delete(temp, index)
right_set.append(new_feature)
else:
new_feature = np.delete(temp, index)
left_set.append(new_feature)
return np.array(left_set), np.array(right_set)
Before generating a decision tree, we define a data structure to save the node in the decision tree:
class DecisionNode:
def __init__(self, index=-1, value=None, results=None, right_tree=None, left_tree=None):
self.index = index
self.value = value
self.results = results
self.right_tree = right_tree
self.left_tree = left_tree
Then, we can generate the decision tree recursively. If there is no feature in the data set, stop. If the information gain is smaller than a given threshold, stop. Else, split the data set according to the best selected feature and its value as shown below:
def createDecisionTree(self, data):
if len(data) == 0:
self.tree_node = DecisionNode()
return self.tree_node
best_gain = 0.0
best_criteria = None
best_set = None
feature_num = len(data[0]) - 1
sample_num = len(data[:, -1])
init_entropy = self.getEntropy(data[:, -1])
for i in range(feature_num):
uniques = np.unique(data[:, i])
for value in uniques:
left_set, right_set = self.divideData(data, i, value)
ratio = float(len(left_set)/sample_num)
if ratio == 0.0:
info_gain = init_entropy - (1 - ratio) * self.getEntropy(right_set[:, -1])
elif ratio == 1.0:
info_gain = init_entropy - ratio*self.getEntropy(left_set[:, -1])
else:
info_gain = init_entropy - ratio * self.getEntropy
(left_set[:, -1]) - (1 - ratio) * self.getEntropy(right_set[:, -1])
if info_gain > best_gain:
best_gain = info_gain
best_criteria = (i, value)
best_set = (left_set, right_set)
if best_gain < self.t:
self.tree_node = DecisionNode(results=self.uniqueCount(data[:, -1]))
return self.tree_node
else:
ltree = self.createDecisionTree(best_set[0])
rtree = self.createDecisionTree(best_set[1])
self.tree_node = DecisionNode(index=best_criteria[0],
value=best_criteria[1], left_tree=ltree, right_tree=rtree)
return self.tree_node
Classify
The principle of classification is like the binary sort tree, namely, comparing the feature value stored in node with the corresponding feature value of the test object. Then, turn to left substree or right substree recursively as shown below:
def classify(self, sample, tree):
if tree.results != None:
return tree.results
else:
value = sample[tree.index]
branch = None
if value >= tree.value:
branch = tree.right_tree
else:
branch = tree.left_tree
return self.classify(sample, branch)
Conclusion and Analysis
There exist pruning process by dynamic programming after generation of decision tree to get the best decision tree. Moreover, Classification and Regression Tree (CART) is a type of decision tree which can be not only applied in classification but also regression. Finally, let's compare our Decision tree with the tree in Sklearn and the detection performance is displayed below:

From the figure, we can learn that the decision tree is not as good as sklearn's, which may be that we don't apply the pruning process.
The related code and dataset in this article can be found in MachineLearning.
