Introduction
As an originally C++ programmer, I miss some aspects of the STL containers which were not implemented in the standard .net collections.
Specifically, the ability to search for an item that is not necessarily in the collection, and get the closest match.
These are the lower_bound and the upper_bound of the std::map.
The need for this functionality (lower_bound and the upper_bound) emerged while trying to display tags along the time axis.
When the view was zoomed, the subset of tags within the zoomed range needed to be fetched. If the set of tags was static, then sorting once and then using
the generic List<> could do the trick, since it provides the BinarySearch method.
However, the set was dynamic, so another approach was needed. Here SortedMap<TKey, TValue> is presented: a generic collection based on the Red Black tree data structure.
It provides lower_bound and upper_bound in addition to the standard collection interface.
If you need the closest match functionality, you are welcome to read ahead and use the code. Even if you don't care about lower/upper bound, you might find the discussion about testing useful,
since it presents some of the primary testing principles, that in my opinion are important for creating robust and (relatively) bug-free software.
Red Black Trees
The Red Black tree is described in many places, so we'll only present it briefly here. It is a binary tree, with each node painted either in black or red (perhaps inspired
by the roulette colors). A red black tree satisfies the following properties:
- Every leaf is black.
- If a node is red, then its children are black.
- Every path from a leaf to the root contains the same number of black nodes.
It is not hard to prove using the properties above that the height of a Red Black tree is O(log n). Hence search for an element is O(log n).
Searching for a closest match, rather than exact match is easy enough: Just search for the element, and if not found, return the node where the search stopped.
Inserting an element into a Red Black tree is composed of two steps:
- First perform a standard binary tree insert. Second fix the the tree so its properties are preserved.
- Removing an element is similar: Standard remove followed by steps to preserve the Red Black properties.
It follows that insertion and removal are also O(log n).
Using the code
SortedMap is composed of 2 layers:
RedBlackTree<T> (in RedBlackTree.cs) - implementation of the Red Black data structure.SortedMap<TKey, TValue> (in SortedMap.cs) - a wrapper of the Red Black tree as a standard collection implementing IDictionary<>,
ICollection<>, and IEnumerable<>.
Other classes in the project:
GenericEnumerator<T> (in GenericEnumerator.cs) - helper for the SortedMap.PermutationGenerator (in PermutationGenerator.cs) - creates all permutations of a specific size: used for testingTreeVisualizer<T> (in TreeVisualizer.cs) - displays the tree in a graphical way: used for testingRedBlackTreeTester (in RedBlackTreeTester.cs) - testing the RedBlackTreeSortedMapTester (in SortedMapTester.cs) - testing the SortedMap
If you need a standard collection - use the SortedMap class, you will need
SortedMap.cs, RedBlackTree.cs, and GenericEnumerator.cs.
If you do not care about standard interfaces use directly the RedBlackTree class - only
RedBlackTree.cs is needed.
RedBlackTree<T> provides the following methods (note that it has only one type argument):
Clear() - empties the treevoid Add(T item) - add a new item to the treevoid Remove(T item) - removes an existing itemTreeNode Find(T item) - find an exact matchTreeNode FindGreaterEqual(T item) - find either an exact match or the next itemTreeNode First() - return the first node in the treeTreeNode Next(T item) - return the next nodebool IsValid() - check whether the tree is a valid Red Black tree (for testing)bool TravelTree(TreeVisitor visitor) - travels the tree and applies the visitor to each node (for testing)
SortedMap<TKey, TValue> provides the closest match functionality in addition to the standard collection methods:
TValue LowerBound(TKey key) - return the first element whose key is no less than the provided keyTValue UpperBound(TKey key) - return the first element whose key is greater than the provided keyIEnumerable<KeyValuePair<TKey, TValue>> LowerBoundItems(TKey key) - return an enumerator starting with the lower bound itemIEnumerable<KeyValuePair<TKey, TValue>> UpperBoundItems(TKey key) - return an enumerator starting with the upper bound item
It is surprising how much code is needed in order to create a standard collection. The SortedMap is almost 1000 lines although it does not contain
any logic - just implementing standard interfaces. The following code snippet demonstrates how to retrieve all items with keys that greater than a particular key:
SortedMap map = new SortedMap<int, double>();
...
int key = someValue;
foreach (KeyValuePair<int, double> pair in map.UpperBoundItems(key))
{
}
Complexity
As mentioned above, insertion removal and search for a key (both exact or closest match) cost O(log n) operations.
Moving to the next element is O(log n) - worst, O(1) - amortized. This means that a single next operation may cost O(log n),
but moving along the whole tree costs O(n) operations, so the average cost for a single operation is O(1). The following table summarizes the complexity of the various operations:
| Operation | Complexity |
|---|
| Insertion | O(log n) |
| Removal | O(log n) |
| Search | O(log n) |
| Next element | O(log n) (amortized O(1)) |
Testing the Tree
The first question that comes to mind when creating this kind of data structure is why this particular choice of colors (Red and Black).
The second question is how to make sure that the structure fulfills its requirements. One answer is validity check.
I added a method IsValid to the RedBlackTree class, that checks the validity of the structure,
and makes sure in particular, that the count of black nodes from every leaf is the same.
During testing, this method is called after each operation in order to locate the exact point when the tree became invalid.
However this is not enough, since the tree may be valid, but contains wrong data.
For this I used the "compare to a simpler data structure" technique. Each operation on the tree was applied also to a List<>.
The content of the tree was compared to the content of the list after each modification - to verify that the content of the tree is correct.
2 automatic tests were used to test the tree:
The first was adding to the tree all permutation of the numbers 1 to 9. The second was to randomly add and remove values to the tree while checking its validity.
I often use this kind of random test since in most cases it will reveal bugs in unexpected situations.
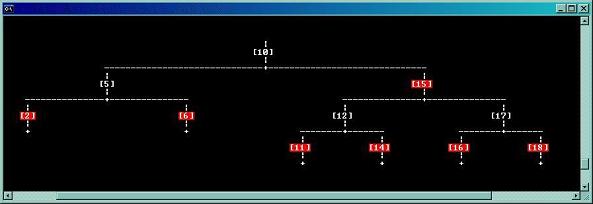
However this was not enough: The IsValid failed and the tree was too complex to understand the problem. Here the TreeVisualizer came to the rescue.
It is a simple class that displays the tree in a text window (You can see a snapshot at the top of the article).
Using it to within the tree implementation greatly helped to pinpoint the problems. So to summarize:
- Validation - Write a method that tests the requirements and invoke it during testing.
- Compare to a simpler structure - If possible, compare the new data structure to a simpler structure (preferably standard).
- Automatic Random Testing - It will reveal situations that you didn't foresee.
- Visualization - It helps to visualize the data structure. Sometimes it's a simple dump and in other times a graphical image.
