Step-by-Step Guide to Implement Machine Learning VI - AdaBoost

Ryukkkk

5.00/5 (1 vote)

20 May 2019CPOL2 min read

Easy to implement machine learning

This article is an entry in our Machine Learning and Artificial Intelligence Challenge. Articles in this sub-section are not required to be full articles so care should be taken when voting.

Introduction

AdaBoost is an approach of Boosting, which is based on the principle that combining multiclassifiers can get a more accurate result in a complex environment.

AdaBoost Model

The AdaBoost model consists of weak classifiers, weight update and classify.

Weak Classifiers

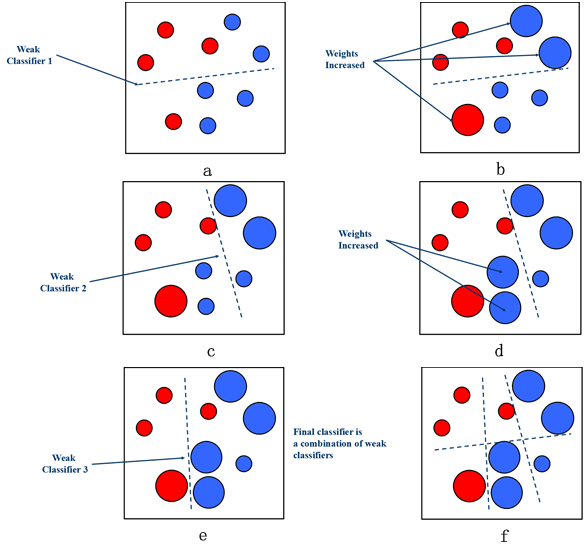
AdaBoost combines weak classifiers with certain strategies to get a strong classifier, as shown below. At each iteration, the weights of samples which are wrongly classified will increase to catch the classifier "attention". For example, in Fig. (a), the dotted line is the classifier-plane and there are two blue samples and one red sample which are wrong classified. Then, in Fig. (b), the weights of two blue samples and one red sample are increased. After adjusting the weights at each iteration, we can combine all the weak classifiers to get the final strong classifier.

Weight Update

There are two types of weight to update at each iteration, namely, the weight of each sample $w_{i}$ and the weight of each weak classifiers $\alpha_{m}$ . At the beginning, there are initialized as follows:

$w_{i}=\frac{1}{N}$

$\alpha_{m}=\frac{1}{M}$

where N, M are the number of samples and the number of weak classifiers respectively.

AdaBoost trains a weak classifier at each iteration denoted as $G_{m}\left(x\right)$ whose training error is calculated as:

$e_{m}=\sum_{i=1}^{N}w_{mi}I\left(G_{m}(x_{i})\ne y_{i}\right)$

Then, update the weight of weak classifier by:

$\alpha_{m}=\frac{1}{2}\ln\frac{1-e_{m}}{e_{m}}$

Update the weights of samples by:

$w_{mi}=\frac{w_{mi}\cdot \exp\left(-\alpha_{m}y_{i}G_{m}\left(x_{i}\right)\right)}{Z_{m}}$

where:

$Z_{m}=\sum_{i=1}^{N}w_{mi}\exp\left(-\alpha_{m}y_{i}G_{m}\left(x_{i}\right)\right)$

From the above equations, we can conclude that:

The training error is the sum of weights of the wrong classified samples.
When e_m is less than 0.5, a_m is greater than 0, which means the lower training error the weak classifiers has, the more important role that weak classifier plays in the final classifier.
The weight update can be written as:
$w_{mi}=\left\{ \begin{aligned} \frac{w_{mi}}{Z_{m}}e^{-\alpha_{m}},G_{m}\left(x_{i}\right)=y_{i}\\ \frac{w_{mi}}{Z_{m}}e^{\alpha_{m}},G_{m}\left(x_{i}\right)\ne y_{i} \end{aligned} \right.$

which means that the weights of right classified samples decrease while the weights of wrong classified samples increase.

The code of training process of AdaBoost is shown below:

Python

def train(self, train_data, train_label):
        if self.norm_type == "Standardization":
            train_data = preProcess.Standardization(train_data)
        else:
            train_data = preProcess.Normalization(train_data)

        train_label = np.expand_dims(train_label, axis=1)
        sample_num = len(train_data)

        weak_classifier = []

        # initialize weights
        w = np.ones([sample_num, 1])
        w = w/sample_num

        # predictions
        agg_predicts = np.zeros([sample_num, 1]) # aggregate value of prediction

        # start train
        for i in range(self.iterations):
            base_clf, error, base_prediction = self.baseClassifier(train_data, train_label, w)
            alpha = self.updateAlpha(error)
            weak_classifier.append((alpha, base_clf))

            # update parameters in page of 139 Eq.(8.4)
            expon = np.multiply(-1 * alpha * train_label, base_prediction)
            w = np.multiply(w, np.exp(expon))
            w = w/w.sum()

            # calculate the total error rate
            agg_predicts += alpha*base_prediction
            error_rate = np.multiply(np.sign(agg_predicts) != train_label, 
                         np.ones([sample_num, 1]))
            error_rate = error_rate.sum()/sample_num

            if error_rate == 0:
                break
            self.classifier_set = weak_classifier
        return weak_classifier

Classify

Combine all the weak classifiers to get a strong classifier. The classify rule is the weighted sum of each weak classifier result, which is given by:

$G\left(x\right)=sign\left(\sum_{m=1}^{M}\alpha_{m}G_{m}\left(x\right)\right)$

Conclusion and Analysis

AdaBoost can be regarded as additive model with exponent loss function using forward forward step algorithm. In AdaBoost, the type of weak classifiers can be different or the same. In this article, we use 5 SVM classifiers as the weak classifiers, and the detection performance is shown below:

It can be that the accuracy increases about 5% and the runtime is about 5 times of the single SVM.

The related code and dataset in this article can be found in MachineLearning.

License

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)