Introduction
In this article we show how odeint can be adapted to work with VexCL.
odeint is a library for solving ordinary differential equations (ODE) numerically with C++. ODEs are important in many scientific areas and hence numerous applications
for odeint can be found. VexCL is a high-level C++ library for OpenCL. Its main feature are expression templates which significantly simplify the way one writes code
for numerical problems. By using OpenCL the resulting code can run on a GPU or can be parallelized on multiple cores. Both libraries have been introduced here on the CodeProject:
Note: This article does not give an introduction to the odeint and ordinary differential equations. If you are unfamiliar with those read the odeint article first!
Note: VexCL needs C++11 features! So you have to compile with C++11 support enabled.
odeint provides a mechanism which lets the user change the way how the elementary numerical computations (addition, multiplication, ...) are performed. This mechanism consist of a combination of state_type, algebra and operations. state_type represents here the state of the ODE and it is usually a vector type like std::vector, std::array. An example is:
std::array< double , 3 > x1 , x2;
odeint::range_algebra algebra;
double dt = 0.1;
algebra.for_each2( x1 , x2 , default_operations::scale_sum1( dt ) );
The algebra is responsible for iterating of all elements of the state whereas the operations are responsible for the elementary operation.
In the above example a for_each2 is used, which means that two state types are iterated. The operation is a scale_sum1
which simply calculates x1[i] = dt * x2[i]. odeint provides a set of predefined algebras:
range_algebra: default algebra which works on Boost.Ranges array_algebra: specialized algebra for boost::arrayfusion_algebra: algebra for compile-time sequences like boost::fusion::vector,
std::tuple, ..., see Boost.Fusionvector_space_algebra: algebra for vector space types which redirect all computations directly to the operations.
thrust_algebra: algebra for Thrust
Many libraries for vector and matrix types provide expression templates for the elementary operations. Examples are Boost.Ublas, MTL4, and VexCL. Such libraries do not need an own algebra but can be used with the vector_space_algebra and the default_operations which simply calls the operations directly on the matrix or vector type. All you have to do in this case is to adapt odeint resizing mechanism. How this works for VexCL is described in this article. The adaption of Boost.Ublas and MTL4 is then very similar to the adaption of VexCL.
Adapting VexCL
VexCL introduces several vector types which live on OpenCL devices. The main vector type is vex::vector which is the classical analog to the std::vector. vex::vector can also be split over multiple devices. One of the major points of VexCL is that is supports expression templates. For example, it is possible to write code like
vex::vector< double > x() , y() , z();
z = 0.125 * ( x * x + 2.0 * x * y + y * y );
The second line in this example creates lazily an expression template which is evaluated when the assign operator is invoked. The advantage is surely that temporaries are avoided and you do not loose any performance.
Since VexCL already supports expression templates it can directly be used with the vector_space_algebra of odeint. There is no need to introduce an additional algebra or new operations. The example from the previous section can be written as
vex::vector< double > x , y;
vector_space_algebra algebra;
double dt = 0.1;
algebra.for_each2( x , y , default_operations::scale_sum1( dt );
In order to use vex::vector with odeint only the resizing of VexCL needs to be adapted for odeint. Resizing in odeint is necessary since many solvers need temporary state types. These state types need to be constructed and initialized which is done by the resizing mechanism of odeint.
The resizing mechanism of odeint consist of three class templates. These classes are is_resizeable<> which is a simply meta function telling odeint if the type is really resizable. The second class is same_size_impl<> which has a static method same_size taking two state_types as arguments and returning if both types have the same size. The third class is resize_impl<> which performs the actual resizing. These classes have a default implementation and can be specialized for any type.
For VexCL the specialization is:
template< typename T >
struct is_resizeable< vex::vector< T > > : boost::true_type { };
template< typename T >
struct resize_impl< vex::vector< T > , vex::vector< T > >
{
static void resize( vex::vector< T > &x1 , const vex::vector< T > &x2 )
{
x1.resize( x2.queue_list() , x2.size() );
}
};
template< typename T >
struct same_size_impl< vex::vector< T > , vex::vector< T > >
{
static bool same_size( const vex::vector< T > &x1 , const vex::vector< T > &x2 )
{
return x1.size() == x2.size();
}
};
That is all. Having the specializations one can use VexCL and odeint. Of course, these specializations are already defined in odeint. You only need to include:
#include <boost/numeric/odeint/external/vexcl/vexcl_resizing.hpp>
VexCL also has a multi-vector, which packs several instances of vex::vector and allows to synchronously operate on all of them. The resizing specializations for the multi-vector are very similar to vex::vector and are also included in the header above.
Examples
The power of GPUs is only used if one tries to solve large problems, such that many sub-problems can be solved in parallel. For ODEs one needs about 10000 coupled ODEs to gain performance from the GPU compared to the CPU. In this section two typical examples for large ODEs are introduced.
In the first example we will use the Lorenz system and study its dependence on one of the parameters. The Lorenz system is a system of three coupled ODEs which shows chaotic behavior for a large range of parameters. The ODE reads
dx / dt = -sigma * ( x - y )
dy / dt = R * x - y - x * z
dz / dt = - b * z + x * y
We will study the dependence on the parameter <coed>R. Therefore, we create a large set of these systems (each with a different parameter R),
pack them all into one system and solve them simultaneously on the GPU. The Lorenz system is a system of three coupled ordinary differential equations. If we want to solve N of these systems the overall state has 3*N entries. We can pack each component separately into one of VexCL's vectors. But multi-vector consisting of three sub-vectors fits this problem much better.
The typedefs are:
typedef vex::vector< double > vector_type;
typedef vex::multivector< double, 3 > state_type;
The vector_type here is needed to store the parameters <coed>R. The sub-vectors of the state_type can be accessed via:
state_type X;
auto &x = X(0);
auto &y = X(1);
auto &z = X(2);
So, all x-components of the N Lorenz system are in X(0), all y-components are in X(1), and all z-components are in X(2). Now, we implement the system function. This function represents the ODE and is used from odeint to solve the ODE. The system needs to be a function object (a functor or a plain C-function) with three parameters. Is signature is void( const state_type&, state_type&, time_type ). The first parameter is an input parameter and represents the current state of the ODE, the second one is an output parameter and is used to store
the RHS of the ode. The third parameter is simply the time. As said above VexCL supports expression templates for numerical computation. By using expression templates the system function becomes very simple.
const double sigma = 10.0;
const double b = 8.0 / 3.0;
struct sys_func
{
const vector_type &R;
sys_func( const vector_type &_R ) : R( _R ) { }
void operator()( const state_type &x , state_type &dxdt , double t ) const
{
dxdt(0) = -sigma * ( x(0) - x(1) );
dxdt(1) = R * x(0) - x(1) - x(0) * x(2);
dxdt(2) = - b * x(2) + x(0) * x(1);
}
};
Note that the system function holds a vector for all parameters R. Each line in system functions computes the expression for the whole set of all N elements of the vector. This is in principle all. We can now instantiate one of odeints solvers and solve the ODE. A complete main program might look like this:
vex::Context ctx( vex::Filter::Type(CL_DEVICE_TYPE_GPU) );
std::cout << ctx << std::endl;
const size_t n = 1024 * 1024;
const double dt = 0.01;
const double t_max = 100.0;
double Rmin = 0.1 , Rmax = 50.0 , dR = ( Rmax - Rmin ) / double( n - 1 );
std::vector<double> r( n );
for( size_t i=0 ; i<n ; ++i ) r[i] = Rmin + dR * double( i );
vector_type R( ctx.queue() , r );
state_type X(ctx.queue(), n);
X(0) = 10.0;
X(1) = 10.0;
X(2) = 10.0;
runge_kutta4<
state_type , double , state_type , double ,
odeint::vector_space_algebra , odeint::default_operations
> stepper;
integrate_const( stepper , sys_func( R ) , X , 0.0 , t_max , dt );
As you can see, odeint's vector_space_algebra and default operation set are used here.
As a second example we choose a chain of coupled phase oscillators. Phase oscillators
are a very simplified version of usual oscillator where the state is described by a 2π periodic variable. If a single phase oscillator is uncoupled its phase φ is described by a linear growth dφ / dt = ω where ω is the phase velocity. Therefore, interesting behavior can only be observed if two or more oscillators are coupled. In fact, a system of coupled phase oscillators is a prominent example of an emergent system where the coupled system shows a more complex behavior than its constitutes.
The concrete example we analyze here is:
dφ(i) / dt = ω(i) + sin( dφ(i+1) - dφ(i) ) + sin( dφ(i) - dφ(i-1) )
Note, that dφ(i) is a function of the time, the argument i denotes here the i.th phase in the chain. To implement such equations efficiently on the GPU Denis did a great job of introducing some kind of generalized stencils. The stencil for our problem is generated by
extern const char oscillator_body[] = "return sin(X[-1] - X[0]) + sin(X[0] - X[1]);";
vex::StencilOperator< double, 3, 1, oscillator_body > S( queue_list() );
The first line simply generates an OpenCL string of the elementary operation done in each kernel. The second line instantiates the stencil operator. It can be applied to a vector x by imposing S(x). The complete system function of the chain of phase oscillators is then
extern const char oscillator_body[] = "return sin(X[-1] - X[0]) + sin(X[0] - X[1]);";
struct sys_func
{
const state_type ω
vex::StencilOperator< double, 3, 1, oscillator_body > S;
sys_func( const state_type &_omega )
: omega( _omega ) , S( _omega.queue_list() )
{ }
void operator()( const state_type &x , state_type &dxdt , value_type t ) const
{
dxdt = omega + S( x );
}
};
Note again, how compact the code is. An equivalent version of the above system with Thrust is much larger. In fact the Lorenz system implementation introduced here as 78 lines of code, whereas the Thrust version has 145. Furthermore, Thrust also needed a separate algebra as well as a separate operations type.
Performance comparison
In this section we compare the performance of VexCL against Thrust. Thrust is a high level library for CUDA which provides a STL like interface to vectors on the CUDA devices. Furthermore, it can easily be used to put the computations on one or more cores of your CPU by using OpenMP. The Lorenz example for Thrust is described in the tutorial of odeint. Thrust does not provide expression templates, but is has an advanced iterator system which lets you program the numerical expression in an easy manner. Nevertheless it is more complicated than VexCL.
The image below shows the performance of the Lorenz system example for several configurations of Thrust and VexCL. In detail it shows the performance of VexCL on one GPU, two GPUs, three GPUs, and on one CPU core. Furthermore, the performance for Thrust on the GPU (only single GPU computations are supported) and on one CPU are shown shown. It is clearly visible that Thrust outperforms VexCL on one GPU. But if more than one GPUs are used (and are installed on your computer) VexCL becomes faster. The same holds for the CPU version. Furthermore, one can clearly see that for small system sizes where the computation time is relatively small VexCL has a constant run-time. This is due to the fact that the OpenCL compiles the kernels at run-time for the GPU. (The right panel shows the performance of VexCL relative to Thrust on GPU. So if the curves are above 1 then VexCL is faster otherwise it is slower.)
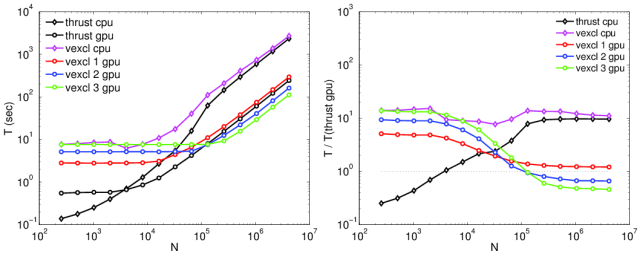
The performance results for the phase oscillator chain are shown in the next figure. For the Thrust version of the chain the system function has been implemented with Thrust's iterator system. Interestingly, VexCL here outperforms Thrust. Of course, for small system sizes the constant overhead is present and here Thrust performs better. But for large systems VexCL becomes faster. This might be due to the fact that the iterators in Thrust have their price but it is not exactly clear why which version is faster.

Conclusion
We have shown how VexCL can be adapted to odeint and how it can be used to increase the performance when solving large ordinary differential equations. Large here means that the system size (number of coupled coupled ODEs) should be of the order 10000-100000 to see a reasonable performance gain compared to usual CPUs. For large systems this gain can be about 20 times.
The performance of VexCL has also been compared against Thrust. In one example a large ensemble of ODEs has been solved. It turns out that Thrust is about 10% faster in this case compared to VexCL. In the second example a system of coupled phase oscillators has been studied. Here VexCL is faster by a factor of 1.2. Nevertheless, the expression templates of VexCL are a big plus for this library. It lets the user solve complicated problems within minutes where the development with native CUDA or OpenCL code or even with Thrust requires much more time.
References
History
- 26.7.2012 - Initial version
