Computational Types in C# and F#

Marc Clifton

4.91/5 (18 votes)

2 Aug 2012CPOL20 min read

93.1K

197

Exploring the concept of Computational Types in both C# and F#

Download ComputationalTypes.zip - 122.7 KB

Introduction

In this article, I will be exploring the concept of "computational types" - types that are associated with computations, and whose computations can be determined via reflection to self-document and automate the value computation, based on type. I will illustrate how to work with computational types in both C# and F# languages.

Type Systems

A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur. The particular type system in question determines exactly what constitutes a type error, but in general the aim is to prevent operations expecting a certain kind of value being used with values for which that operation does not make sense (logic errors); memory errors will also be prevented. Type systems are often specified as part of programming languages, and built into the interpreters and compilers for them; although they can also be implemented as optional tools.¹

The salient part of the above quote is the first sentence: "a type system associates a type with each computed value." In this article, I will explore the concept that not only is a type associated with a computed value, but that the computation of the value is itself is determined by the type, and I will demonstrate this concept in both C# and F# code.

Primitive Types

Primitive types (int, double, bool, etc., do not provide sufficient specification to derive anything other than the most basic computations / validations. In databases, for example, most validations require additional fields such as foreign key relationships, length, pattern matching, and triggers that further define the validation to be performed on the primitive type. Computations in a database are handled by SQL expressions, PL/SQL code, or client/server-side custom code, all of which evaluate to a primitive type or a collection (table) of primitive types.

Higher Order Types: Classes and Structs

While we almost always work in an object-oriented paradigm, we rarely create distinct (non-primitive) types for discrete fields within a class. This reduces the type safety of the program. Another artifact of working too closely with primitive types is that the code responsible for computations/validations on a type are difficult to locate, extend, and test. More on this topic will be discussed later.

Also, because classes and structs tend to be used to encapsulate the entire concept of an "object," they are not typically seen as a mechanism for providing exact type specification. For example, you may see something like this:

public class FullName
{
  public string FirstName {get; set;}
  public string LastName {get; set;}
}

but rarely will you see this:

public class FullName
{
  public TFirstName FirstName {get; set;}
  public TLastName LastName {get; set;}
}

where TFirstName and TLastName are simple type-specific implementations wrapping a string value. There obviously is a layer of complexity that is added with this latter approach, sacrificing type safety and computability for the easier syntax.

Church's Type Theory

Type theories are also called higher-order logics, since they allow quantification not only over individual variables (as in first-order logic), but also over function, predicate, and even higher order variables. Type theories characteristically assign types to entities, distinguishing, for example, between numbers, set of numbers, functions from numbers to sets of numbers, and sets of such functions...these distinctions allow one to discuss the conceptually rich world of sets and functions without encountering the paradoxes of naive set theory.²

By distinguishing values (numbers, strings, etc.) using unique types, the program can more easily express functions, in a completely type-safe manner, that operate on those unique types. Furthermore, program inspection (automated with reflection) can build a dictionary of functions that operate on the discrete types. For example, this function (intentionally obfuscated):

string X(string s1, string s2);

tells the programmer nothing other than that method X takes two strings and returns a string. Conversely:

TFullname X(TFirstName s1, TLastName s2);

tells the programmer that method X takes two types, TFirstName and TLastName, and returns a TFullName type. This is much more descriptive even though the method name and variable names are obfuscated. Furthermore, by reflection, the programmer can ask:

what are all the functions that use type T?
what are all the functions that compute type Q?

This begins to approach what the quote above is referring to with regards to allowing "one to discuss the conceptually rich world of sets and functions."

Computational Type Theory

A salient feature of computational type theory is that it has been publicly implemented and used to do hard work, especially in computer science. What does this mean? To say that a logical theory has been publicly implemented means that the following were accomplished: (1) Every detail of the theory was programmed, creating a software system (called by various names such as: a theorem prover, prover, proof assistant, proof checker, proof development system, logical programming environment, logic engine). (2) Many people used the system to find, check, and publish hundreds of proofs (3) Articles and books were published about the formal theory, its system, and how to use it. This kind of formalization in extremis became possible only in the 20th century and will be common in the 21st century as such theories advance computer assisted thought.

The scientific work done using an implemented computational type theory (CTT) includes finding new algorithms, building software systems that are correct-by-construction, solving open problems in mathematics and computing theory, providing formal semantics for modern programming languages (including modules, dependent records, and objects) and for natural languages, automating many tasks needed to verify and explain protocols, algorithms, and systems, and creating courseware that is grounded in fully formalized and computer checked explanations of key computing concepts.³

Consider what this quote is suggesting to -- the formalization of computational type theory "will be common in the 21st century." While there is considerable information on type theory, formal methods, theorem provers, etc., this so far has been in the domain mainly of mathematicians and obscure functional programming environments such as Coq¹⁰. Even Microsoft is researching verifiably secure program construction and proofs with F*¹¹. Currently this work is being applied mostly to improving security and creating provably correct algorithms. Personally, I think that computational types is a rich area to explore in improving code quality, accuracy, and maintainability (even if those buzzwords have gotten moldy over the last 30 years.) The purpose of this article is to introduce these concepts in a hopefully simple and easy to understand manner.

Dependent Types

In computer science and logic, a dependent type is a type that depends on a value. Dependent types play a central role in intuitionistic type theory and in the design of functional programming languages like ATS, Agda and Epigram.

An example is the type of n-tuples of real numbers. This is a dependent type because the type depends on the value n.

Deciding equality of dependent types in a program may require computations. If arbitrary values are allowed in dependent types, then deciding type equality may involve deciding whether two arbitrary programs produce the same result; hence type checking may become undecidable.

The Curry–Howard correspondence implies that types can be constructed that express arbitrarily complex mathematical properties. If the user can supply a constructive proof that a type is inhabited (i.e., that a value of that type exists) then a compiler can check the proof and convert it into executable computer code that computes the value by carrying out the construction. The proof checking feature makes dependently typed languages closely related to proof assistants. The code-generation aspect provides a powerful approach to formal program verification and proof-carrying code, since the code is derived directly from a mechanically verified mathematical proof.¹²

The concept of dependent types is outside of the scope of this article, but I mention it here because it adds a particular nuance to the idea of computational types - the type itself is dependent on the value. Consider however a simple case, where we have a table of addresses and a lookup field indicating whether the address is a PO Box, residential street, or commercial address. The type that is instantiated depends on the value of the lookup field. Or, a more simple example, consider a field with the possible values of 2, .33333, or 3.1415. Here we might instantiate the type "integer", "rational", or "irrational" respectively, depending on the value.

Defining The Problem: Types vs. Instances

Another way to state the problem of types vs. instances is "classes vs. objects." Classes are, of course, types, and objects are instances of classes. Regardless though of the terminology, the question is: How do we perform type-based computations? Obviously, the computations have to be performed on values, but is the specification for the computation determined by the type? Sort of. While this looks like a straight forward "type with member functions" solution, let's look at this more closely.

A Simple Example: Compute Full Name

Let's say we have these three types:

FirstName, with an instance "Marc"
LastName, with an instance "Clifton"
FullName, a computed type whose result is "Clifton, Marc"

To state this more abstractly:

We have a specification for a computed type that operates on the instances of two other types. The result of the computation should be an instance of the computed type.

And concretely:

Given instances of two types, FirstName and LastName, the computed type FullName should be a concatenation of LastName and FirstName, separated by a ", ". (This of course is specific only to certain societies.)

This might seem very simple at first:

public class FullName

{
  public string Compute(string firstName, string lastName)
  { return lastName + ", " + firstName; }
}

The problem here is that we have to first instantiate FullName in order to perform the computation:

FullName fn = new FullName();
string fullName = fn.Compute("Marc", "Clifton");

The problem is slightly improved by using a static method:

public static class FullName
{
  static string Compute(string firstName, string lastName)
  { return lastName + ", " + firstName; }
}

string fullName = FullName.Compute("Marc", "Clifton");

But we still have a few problems:

The computation returns a primitive type, not the desired type, FullName.
The computation's parameters are strings, not the types FirstName and LastName

Because these are primitive types, we have no type checking to ensure that the programmer doesn't get the order of the first and last name reversed:

string fullName = FullName.Compute("Clifton", "Marc");

Type vs. Instance: Summary of Issues

The above discussion can be summarized into four issues:

We have a computed type, and the computation on that type should return an instance of that type
We want to exactly specify the parameter types on which the computation operates to avoid incorrect computations
We need to somehow associate the computed type to its computational function
We need to somehow associate the fact that, given the instances LastName and FirstName, we can actually compute FullName

We will address these issues, beginning with how to define types exactly.

Defining Types Exactly

Our first inclination to exactly define the types FirstName, LastName, and FullName might be to attempt this in C#:

public class FirstName : String {}

which of course fails with: cannot derive from sealed type 'string'

In F#, we might be inclined to try this:

type FirstName = string

which is useless because "Type abbreviations are not preserved in the .NET Framework MSIL code. Therefore, when you use an F# assembly from another .NET Framework language, you must use the underlying type name for a type abbreviation."⁴ and therefore does not actually provide usable type specification.

C# Example

This leads us to this form, in C#:

public class FirstName
{
  public string Value { get; set; }
}

public class LastName
{
  public string Value { get; set; }
}

public class FullName
{
  public string Value { get; set; }
}

static FullName ComputeFullName(FirstName fn, LastName ln)
{
  return new FullName() { Value = ln.Value + ", " + fn.Value };
}

F# Example

In F#, this can be implemented with records the following types:

type typeFirstName =
{
    FirstName : string;
}

type typeLastName = 
{
    LastName : string;
}

type typeFullName = 
{
    FullName : string;
}

let ComputeFullName fn ls = 
    {FullName = ls.LastName + ", " + fn.FirstName}

Note the difference though - in the C# code, we could use the property "Value" in each class. In the F# code, because of the types are inferred, the record's labels must be unique.

A Comment About Type Inference in Functional Programming Languages

Failing to use unique labels in a record can lead to type inference confusion and has caused a considerable amount of wasted time, at least on the part of this developer! And given that in F# (as well as other functional programming languages like OCaml) the type inference does not look at the entire record instantiation to determine the type, it is very important that the first label in a record is unique from all other labels in other records. Otherwise, most likely, the type inference will result in the wrong type.

In F# Interactive (fsi), we can inspect the types for ComputeFullName, observing that the function takes FirstName and LastName types as inputs and returns a FullName type.

val ComputeFullName : typeFirstName -> typeLastName -> typeFullName

This is "obvious by inspection" in the C# method:

static FullName Compute(FirstName fn, LastName ln)

Calling the Computation

In C#, we can invoke our computation with something like this:

static void Main(string[] args)
{
  FirstName fn = new FirstName() { Value = "Marc" };
  LastName ln = new LastName() { Value = "Clifton" };
  FullName name = ComputeFullName(fn, ln);
  Console.WriteLine(name.Value);
}

and in F#:

let fn = {FirstName = "Marc"}
let ln = {LastName = "Clifton"}
let result = ComputeFullName fn ln
printfn "%s" result.FullName

With Regards to Currying

Currying is a feature of functional programming languages that lets you define partial functions. For example:

let fn = {FirstName = "Marc"}
let ln = {LastName = "Clifton"}
let partialResult = ComputeFullName fn
let fullResult = partialResult ln
printfn "%s" fullResult.FullName

The reason it's important to consider currying is that, while it is possible to specify function parameter types, this should be avoided whenever possible. Specifying function parameter types causes the compiler to treat the parameter list as a tuple, which disables currying.⁵

For example:

let ComputeFullName(fn : typeFirstName, ls : typeLastName) = 
    {FullName = ls.LastName + ", " + fn.FirstName}

let fn = {FirstName = "Marc"}
let ln = {LastName = "Clifton"}
let result = ComputeFullName(fn, ln)
let partialResult = ComputeFullName(fn)

Results in a compiler error in the last statement:

This expression was expected to have type typeFirstName * typeLastName but here has type typeFirstName

Note how the compiler is now expecting a tuple typeFirstName * typeLastName as the parameter list, which disables currying. This is not desirable, as currying is an important component of functional programming.

As Matt Newport pointed out in the comments to this article, this syntax allows one to specify parameter types and still preserve the ability to curry:

let Add (a:float) (b:float) = a + b
let AddPartial = Add 1.0 
printfn "%f" (AddPartial 2.0)

Thus we avoid using the tupled parameters but still support currying. As a personal note, I find it odd that I did not come across this example in any of my searches for specifying parameter types.

A Comment About Currying

In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments (or an n-tuple of arguments) in such a way that it can be called as a chain of functions each with a single argument (partial application). It was discovered by Moses Schönfinkel[1] and later re-discovered by Haskell Curry.⁷

Granted, Wikipedia is not to be taken as an authority on the subject, but I am disturbed by the word "discovered," as it implies that this was not an intentional feature but rather a "discovered" artifact. As such, since it was not intentional, perhaps the emphasis on currying is a bit overblown. Patrick Hurst, with regards to Haskell, writes "Furthermore, without currying, you couldn’t have variadic functions."⁸ Variadic functions are functions that take a variable number of parameters, and this is easily supported in imperative programming languages, for example, with C#'s params keyword.

In Haskell, every function takes a single argument. A function of multiple arguments, such as map, which applies a function to every element in a list, actually only has one argument; for example, map can be interpreted either as taking a function and a list and returning a list, or as taking a function and returning a function that takes a list and returns a list...This process, of taking a multi-argument function and converting it into a series of single-argument functions is known as currying...the process of partially applying arguments to a function in this way is known as ‘partial application’, but is also called currying.⁸

With Regards to Overloaded Functions/Methods

It would be useful to allow both the programmer to specify the first and last names in either order. In C#, we can easily achieve this:

static FullName Compute(FirstName fn, LastName ln)
{
  return new FullName() { Value = ln.Value + ", " + fn.Value };
}

static FullName Compute(LastName ln, FirstName fn)
{
  return new FullName() { Value = ln.Value + ", " + fn.Value };
}

Unfortunately, in F#, we cannot. This:

let ComputeFullName fn ls = 
    {FullName = ls.LastName + ", " + fn.FirstName}

let ComputeFullName ls fn =
    {FullName = ls.LastName + ", " + fn.FirstName}

Results in the compiler error: Duplicate definition of value 'ComputeFullName'. Don Syme writes:

Adhoc overloading of unqualified function names was considered as part of the design of F#. However, we rejected it on software engineering grounds.

As you would appreciate, adhoc overloading can be a blessing and a curse. In C# and .NET overloading is relatively "tamed" primarily because all references to overload sets are qualified by a type name, e.g. C.M, rather than just M (except in the body of C, which is somewhat different). In F# we chose to follow a similar approach: permit method overloading, but ensure that references to overloaded things are qualified by (type) names. We expect this restriction to continue.⁶

However, this implementation, as member functions, fails:

type typeFullName = 
    {
        FullName : string;
    }
    static member Compute fn ls =
        {FullName = ls.LastName + ", " + fn.FirstName}
    static member Compute ls fn = 
        {FullName = ls.LastName + ", " + fn.FirstName}

Resulting in the error

The method 'Compute' has curried arguments but has the 
same name as another method in this type. Methods with curried arguments cannot 
be overloaded. Consider using a method taking tupled arguments.

A Comment About Function Overloading

So, we have the same problem - overloaded functions:

Must be implemented as member functions
Must use the tuple form for parameters

and therefore disables currying, which is supposed to be a useful functional programming feature. This would appear to restrict the usability of F#. If "Overloading is typically the bugaboo of type-inferenced languages (at least when, like F#, the type system isn't powerful enough to contain type-classes)"⁹ and in particular, if overloaded functions must be implemented with tupled parameters, disabling currying, then this imposes a restriction that reduces the usability of the language. Conversely, the whole reason tupled parameters (and member functions) exists in F# is for compatibility with other .NET languages. In and of itself, having uniquely named functions instead of relying on function overloading can be viewed as a positive thing, improving code readability.

What Have We Achieved So Far?

At this point, we have essentially solved the four problems identified earlier.

We have exactly specified our types using C# classes or F# records.
This allows us to create methods/functions (computations) on those exact types, vastly improving type safety.
The return type is an exact specification of a computation that results in the desired type.
If we were to use reflection to inspect the return type, we could determine all the possible computations that result in a specific type. Thus, we can create a dictionary of "type computations."

What we need now is some glue to put the pieces together, namely, determining what computations can be performed given a set of instances and the desired output type. I am reminded of the very first article I ever wrote for Code Project, "Organic Programming Environment", in which I wrote:

Processing functions register themselves with the D-Pool Manager (DPM), indicating the data on which they operate, and the data that they produce.

A better way to phrase this would have been:

A dictionary of computations is created that defines the input types and the resulting output type. Given a set of instantiated types, we can determine the computations that results in desired output type.

We will look next at how to glue the pieces together.

A More Interesting Example: Computations on Zip Code

To demonstrate the concept described so far, let's look at a common data type, the zip code. We are going to specify the following computations on zip code, using a couple web services:

Look up city and state from a zip code
Look up the expected low and high temperatures from a zip code

Defining The Types

First, we need some concrete types.

C#

public class TZipCode
{
  public string ZipCode { get; set; }
  public override string ToString() { return ZipCode; }
}

public class TMinTemp
{
  public double MinTemp { get; set; }
  public override string ToString() { return MinTemp.ToString(); }
}

public class TMaxTemp
{
  public double MaxTemp { get; set; }
  public override string ToString() { return MaxTemp.ToString(); }
}

public class TMinMaxTemp
{
  public TMinTemp MinTemp { get; set; }
  public TMaxTemp MaxTemp { get; set; }
  public override string ToString() { return "(" + MinTemp.ToString() + ", " + MaxTemp.ToString() + ")"; }
}

public class TCity
{
  public string City { get; set; }
  public override string ToString() { return City; }
}

public class TState
{
  public string State { get; set; }
  public override string ToString() { return State; }
}

public class Location
{
  public TCity City { get; set; }
  public TState State { get; set; }
  public override string ToString() { return "(" + City.ToString() + ", " + State.ToString() + ")"; }
}

In the above code, note that I have also created explicit types for City and State. We will see why this is next.

F#

type TZipCode =
    {
        ZipCode : string;
    }
    override this.ToString() = this.ZipCode

type TMinTemp =
    {
        MinTemp : double;
    }
    override this.ToString() = this.MinTemp.ToString()

type TMaxTemp =
    {
        MaxTemp : double;
    }
    override this.ToString() = this.MaxTemp.ToString()

type TMinMaxTemp =
    {
        // note the unique label, which helps type inference.
        AMinTemp : TMinTemp;
        AMaxTemp : TMaxTemp;
    }
    override this.ToString() = "(" + this.AMinTemp.MinTemp.ToString() + ", " + this.AMaxTemp.MaxTemp.ToString() + ")"

type TCity =
    {
        City : string;
    }
    override this.ToString() = this.City

type TState = 
    {
        State : string;
    }
    override this.ToString() = this.State

type Location =
    {
        // note the unique label, which helps type inference.
        ACity : TCity;
        AState : TState;
    }
    override this.ToString() = "(" + this.ACity.City + ", " + this.AState.State + ")"

Defining The Computations

Next, we define the computations.

C#

public static TMinMaxTemp ComputeMinMaxTemp(TZipCode zipCode)
{
  double minTemp;
  double maxTemp;

  AcquireMinMaxTemp(zipCode.ZipCode, out minTemp, out maxTemp);

  return new TMinMaxTemp()
  {
    MinTemp = new TMinTemp() { MinTemp = minTemp },
    MaxTemp = new TMaxTemp() { MaxTemp = maxTemp }
  };
}

public static TMinTemp ComputeMinTemp(TMinMaxTemp temp)
{
  return temp.MinTemp;
}

public static TMaxTemp ComputeMaxTemp(TMinMaxTemp temp)
{
  return temp.MaxTemp;
}

public static TLocation ComputeLocation(TZipCode zipCode)
{
  string city;
  string state;

  AcquireLocation(zipCode.ZipCode, out city, out state);

  return new TLocation()
  {
    City = new TCity() { City = city },
    State = new TState() { State = state }
  };
}

public static TCity ComputeCity(TLocation location)
{
  return location.City;
}

public static TState ComputeState(TLocation location)
{
  return location.State;
}

private static void AcquireMinMaxTemp(string zipCode, out double minTemp, out double maxTemp)
{
  ndfdXML weather = new ndfdXML();
  string latLonXml = weather.LatLonListZipCode(zipCode);
  XDocument xdoc = XDocument.Parse(latLonXml);
  string[] latLon = xdoc.Element("dwml").Element("latLonList").Value.Split(',');
  decimal lat = Convert.ToDecimal(latLon[0]);
  decimal lon = Convert.ToDecimal(latLon[1]);
  string weatherXml = weather.NDFDgenByDay(lat, lon, DateTime.Now, "1", "e", "24 hourly");
  xdoc = XDocument.Parse(weatherXml);

  minTemp = Convert.ToDouble(xdoc.Element("dwml").Element("data").Element("parameters").Elements("temperature").
		Where(el => el.Attribute("type").Value == "minimum").
			Single().Element("value").Value.Trim());
  maxTemp = Convert.ToDouble(xdoc.Element("dwml").Element("data").Element("parameters").Elements("temperature").
		Where(el => el.Attribute("type").Value == "maximum").
			Single().Element("value").Value.Trim());
}

private static void AcquireLocation(string zipCode, out string city, out string state)
{
  USZip zip = new USZip();
  XmlNode node = zip.GetInfoByZIP(zipCode);
  XDocument xdoc = XDocument.Parse(node.InnerXml);
  city = xdoc.Element("Table").Element("CITY").Value;
  state = xdoc.Element("Table").Element("STATE").Value;
}

In the above code, the primitive types in ComputeMinMaxTemp and ComputeLocation are used internally to interface with the web services. Similarly, the primitive types used in the "Acquire..." methods (currently just stubs) are strictly for interfacing with the web services and are not intended to be called directly by consumers of the library defining the computations. This is enforced by the public and private access qualifiers on the static methods.

F#

// Refer to http://codebetter.com/matthewpodwysocki/2009/06/11/f-duck-typing-and-structural-typing/
let inline implicit arg =
    ( ^a : (static member op_Implicit : ^b -> ^a) arg)
let (!!) : string -> XName = implicit

// Webservice Support:

let AcquireMinMaxTemp zipCode =
    let weather = new ndfdXML();
    let latLonXml = weather.LatLonListZipCode(zipCode)
    let xdoc = XDocument.Parse(latLonXml)
    let latLon = xdoc.Element(!!"dwml").Element(!!"latLonList").Value.Split(',');
    let lat = Convert.ToDecimal(latLon.[0]);
    let lon = Convert.ToDecimal(latLon.[1]);
    let weatherXml = weather.NDFDgenByDay(lat, lon, DateTime.Now, "1", "e", "24 hourly");
    let xdoc = XDocument.Parse(weatherXml);

    let minTemp = Convert.ToDouble(xdoc.Element(!!"dwml").Element(!!"data").Element(!!"parameters").Elements(!!"temperature").Where(fun el -> (el : XElement).Attribute(!!"type").Value = "minimum").Single().Element(!!"value").Value.Trim())
    let maxTemp = Convert.ToDouble(xdoc.Element(!!"dwml").Element(!!"data").Element(!!"parameters").Elements(!!"temperature").Where(fun el -> (el : XElement).Attribute(!!"type").Value = "maximum").Single().Element(!!"value").Value.Trim())
    (minTemp, maxTemp)

let AcquireLocation zipCode =
    let zip = new USZip()
    let node = zip.GetInfoByZIP(zipCode)
    let xdoc = XDocument.Parse(node.InnerXml)
    let city = xdoc.Element(!!"Table").Element(!!"CITY").Value
    let state = xdoc.Element(!!"Table").Element(!!"STATE").Value
    (city, state)

// Computations:

let ComputeMinMaxTemp zipCode =
    let minMaxTemp = AcquireMinMaxTemp zipCode.ZipCode 
    {
        AMinTemp = {MinTemp = fst(minMaxTemp) }
        AMaxTemp = {MaxTemp = snd(minMaxTemp) }
    }

let ComputeMinTemp minMaxTemp = {MinTemp = minMaxTemp.AMinTemp.MinTemp}

let ComputeMaxTemp minMaxTemp = {MaxTemp = minMaxTemp.AMaxTemp.MaxTemp}

let ComputeCity location = {City = location.ACity.City}

let ComputeState location = {State = location.AState.State}

let ComputeLocation zipCode =
    let location = AcquireLocation zipCode.ZipCode
    {
        ACity = {City = fst(location) }
        AState = {State = snd(location) }
    }

Dependencies

Note the computational dependency:

Given TZipCode, TLocation can be computed
Given TZipCode, TMinMaxTemp can be computed
Given TLocation, TCity and TState can be computed
Given TMinMaxTemp, TMinTemp and TMaxTemp can be computed

The computational dependencies ensure that types are computed only when their instances are available. A simple mapping of computed types and their input types suffices for purposes of this article:

C#

public struct ComputedType
{
  public Type Type { get; set; }
  public MethodInfo Method { get; set; }
}

static Dictionary<ComputedType, List<Type>> computedTypes;

F#

type ComputedType =
{
    Type : Type
    Method : MethodInfo
}

let computedTypes = new Dictionary<ComputedType, List<Type>>()
let typeInstances = new Dictionary<Type, Object>()

We can then use reflection to populate this dictionary:

C#

static void CreateComputationalTypeDictionary()
{
  computedTypes = new Dictionary<ComputedType, List<Type>>();
  AddToComputedTypesDictionary(typeof(TMinMaxTemp));
  AddToComputedTypesDictionary(typeof(TMinTemp));
  AddToComputedTypesDictionary(typeof(TMaxTemp));
  AddToComputedTypesDictionary(typeof(TLocation));
  AddToComputedTypesDictionary(typeof(TCity));
  AddToComputedTypesDictionary(typeof(TState));
}

static void AddToComputedTypesDictionary(Type t)
{
  GetComputationsFor(t).ForEach(mi =>
  computedTypes.Add(
  new ComputedType()
  {
    Type = mi.ReturnType,
    Method = mi
  },
  new List<Type>(mi.GetParameters().ToList().Select(p => p.ParameterType))));
}

static IEnumerable<MethodInfo> GetComputationsFor(Type t)
{
  return
    from type in Assembly.GetExecutingAssembly().GetTypes()
      from mi in type.GetMethods(BindingFlags.Public | BindingFlags.Static)
        where
          mi.ReturnType == t
      select mi;
}

F#

let GetComputationsFor t =
    seq {
        for typ in Assembly.GetExecutingAssembly().GetTypes() do
            for mi in typ.GetMethods(BindingFlags.Public ||| BindingFlags.Static) do
                match mi with
                    | rt when rt.ReturnType = t ->
                        yield mi
                    | _ -> ()
        }

let AddToComputedTypesDictionary t =
    GetComputationsFor(t).ForEach(fun mi ->
        computedTypes.Add(
            {
                Type = mi.ReturnType
                Method = mi
            },
            new List<Type>(mi.GetParameters().ToList().Select(fun p -> (p : ParameterInfo).ParameterType))))
    |> ignore

let CreateComputationalTypeDictionary =
    AddToComputedTypesDictionary typeof<TMinMaxTemp>
    AddToComputedTypesDictionary typeof<TMinTemp>
    AddToComputedTypesDictionary typeof<TMaxTemp>
    AddToComputedTypesDictionary typeof<TLocation>
    AddToComputedTypesDictionary typeof<TCity>
    AddToComputedTypesDictionary typeof<TState>
    |> ignore

We can then iterate through the dictionary, performing computations on types that are "inhabited" (to use the phrase in the quote on Dependent Types), that is to say, have values associated with them:

C#

static Dictionary<Type, object> typeInstances;

static void ComputeAll()
{
  bool more;
  do
  {
    more = Compute();
  } while (more);
}

static bool Compute()
{
  bool more = false;

  foreach (KeyValuePair<ComputedType, List<Type>> kvpComputation in computedTypes)
  {
    if (!IsTypeComputed(kvpComputation.Key.Type))
    {
      List<object> parms = GetParameterValues(kvpComputation.Value);

      // If we have all the required parameters to perform the computation...
      if (parms.Count == kvpComputation.Value.Count)
      {
        object ret = kvpComputation.Key.Method.Invoke(null, parms.ToArray());
        typeInstances[kvpComputation.Key.Type] = ret;
        more = true;
      }
    }
  }

  return more;
}

/// <summary>
/// Returns true if the type has been computed and a value is associated with the type.
/// </summary>
static bool IsTypeComputed(Type t)
{
  return typeInstances.ContainsKey(t);
}

/// <summary>
/// Returns the computed value for the given type.
/// </summary>
static object GetComputedValue(Type t)
{
  return typeInstances[t];
}

static List<object> GetParameterValues(List<Type> paramTypes)
{
  List<object> ret = new List<object>();

  paramTypes.Where(t => IsTypeComputed(t)).ForEach(t => ret.Add(GetComputedValue(t)));

  return ret;
}

F#

let IsTypeComputed t = typeInstances.ContainsKey(t)

let GetComputedValue t = typeInstances.[t]

let GetParameterValues(paramTypes : List<Type>) =
    let ret = new List<Object>()
    paramTypes.Where(fun t -> IsTypeComputed(t)).ForEach(fun t -> ret.Add(GetComputedValue(t)))
    ret

let Compute computedTypes =
    let mutable more = false
    for kvpComputation in (computedTypes : Dictionary<ComputedType, List<Type>>) do
        match IsTypeComputed kvpComputation.Key.Type with
            | false ->
                let parms = GetParameterValues(kvpComputation.Value)
                match parms.Count with
                    | cnt when cnt = kvpComputation.Value.Count ->
                        let ret = kvpComputation.Key.Method.Invoke(null, parms.ToArray())
                        typeInstances.[kvpComputation.Key.Type] <- ret
                        more <- true
                    | _ -> () // ignore
            | true -> () // ignore
    more

let ComputeAll computedTypes =
    let mutable more = true
    while more do
        more <- Compute computedTypes
    typeInstances

The Results

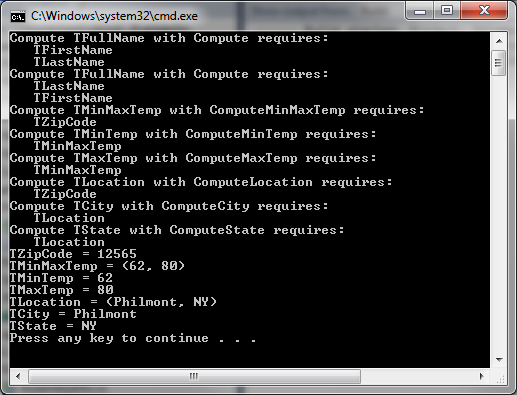
We can do a dump of the dictionary, revealing the computations:

And, by "inhabiting" the TZipCode type, we can perform all the computations necessary to compute the expected min/max temperature and obtain the city and state associated with the zip code:

C#

typeInstances = new Dictionary<Type, object>();
TZipCode zipCode = new TZipCode() { ZipCode = "12565" };
typeInstances.Add(zipCode.GetType(), zipCode);
ComputeAll();
DumpTypeInstances();

F#

In F#, we define a method we can call from C#:

let RunFSharpExample strZipCode =
    typeInstances.Add(typeof<TZipCode>, { ZipCode = strZipCode })
    ComputeAll computedTypes

and invoke the method from C# easily enough:

Dictionary<Type, object> fsTypeInstances = ComputationalTypeExample.RunFSharpExample("12565");
DumpTypeInstances(fsTypeInstances);

Resulting in:

Next Steps

It should be obvious that this is demonstration code. A few things that would need to be polished:

Eliminate the Method.Invoke reflection call
Cache the web services
Create a true dependency tree
The F# code, particularly the Compute method, is too imperative, with the "for" loop
The F# code should be modified to native collections rather than the .NET collection classes
If we improve the F# code to work with immutable data structures, we can easily take advantage of executing computations in parallel

Also, the code above is more of a "push" implementation - given an inhabited type, it iterates through all the possible computations until no further computations can be performed. Realistically, what we want is more of a "pull" implementation: we have certain inhabited types and we want to compute the values of other types. This implementation would require traversing a tree to determine the intermediate computations necessary to arrive at the desired computation.

F# Best Practices

From this exercise, we can arrive at several best practices with the F# language:

Use unique labels in records to ensure correct type inference
#1 helps us avoid typed parameters so that the currying feature is available
Do not use function overloading, instead, provide unique and specific names for functions
Functions in F# that do not take parameters are evaluated immediately, essentially as static initializers. Functions are normally expected to take parameters. In the F# code in this article, I am using a couple statically defined dictionaries, and in order to prevent certain F# functions from executing before the dictionaries are initialized, I have to pass the dictionaries in to the functions. Care needs to be taken with F# regarding parameterless functions, realizing that these will be invoked immediately, before your call into F# executes, and may have unintentional consequences.

Conclusion

Hopefully this article has illustrated some of the basic concepts of computational types in a down-to-earth, easy to understand approach. Writing programs that are expressive in the manner I have described above, while more verbose than typical implementations, results in a much more self-documenting, type safe, and maintainable code base. Certainly however, the use of method invocation is a significant performance penalty that must be addressed for this approach to be useable. This article also demonstrates C# calling F# functions and the use of two webservices, called from both C# and F#.