Welcome back to a new post on thoughts-on-cpp.com. This time, I would like to have a closer look at root approximation methods which I regularly use to solve numerous numerical problems. We start with an easy approach using Bisection, investigating in Newton and Secant method and are concluding with black-box methods of Dekker and Brent.
Preamble
In the following chapters, we have a closer look at several algorithms used for root approximation of functions. We will compare all algorithms against the nonlinear function 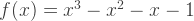 which has only one root inside a defined range [a,b] (this criterion is quite important, otherwise it might be hard to tell which solution we got from the algorithm). An additional criteria is defined by
which has only one root inside a defined range [a,b] (this criterion is quite important, otherwise it might be hard to tell which solution we got from the algorithm). An additional criteria is defined by  . Please keep in mind that we don’t check against the number of iterations we run. This might be necessary because we usually don’t want to run infinite loops. As usual, you can find all the sources at GitHub.
. Please keep in mind that we don’t check against the number of iterations we run. This might be necessary because we usually don’t want to run infinite loops. As usual, you can find all the sources at GitHub.
Bisection Method
Let’s start with a method which is mostly used to search for values in arrays of every size, Bisection. But it can be also used for root approximation. The benefits of the Bisection method are its implementation simplicity and its guaranteed convergence (if there is a solution, bisection will find it). The algorithm is rather simple:
- Calculate the midpoint
 of a given interval [a,b]
of a given interval [a,b] - Calculate the function result of midpoint m, f(m)
- If new m-a or |f(m)| is fulfilling the convergence criteria, we have the solution m
- Comparing sign of f(m) and replace either f(a) or f(b) so that the resulting interval is including the sought root

Implementation of Bisection Algorithm
As we can see from the source code, the actual implementation of Bisection is so simple that most of the code is just there to produce the output. The important part is happening inside the while loop which is executing as long as the result of f(x) is not fulfilling the criteria  . The new position x is calculated in method
. The new position x is calculated in method calculateX() which is checking the sign of f(x) and, depending on its result, assigning x to a or b to define the new range which is including the root point. It is important to note is that the Bisection algorithm needs always results of f(a) and f(b) with different signs which is assured by the method checkAndFixAlgorithmCriteria(). The algorithm is rather slow with 36 iterations to reach the convergence criteria of  , but it will converge with enough given time, regardless what happens.
, but it will converge with enough given time, regardless what happens.

Newton Method
As long as we also have the derivative of the function and the function is smooth, we can use the much faster Newton method where the next closer point to root  can be calculated by:
can be calculated by:


Implementation of Newton Algorithm
Also, this algorithm is iterating as long as the result of f(x) is not fulfilling the criteria  . The method
. The method calculateX() is not only applying the formula of the Newton method, but it is also checking if the derivative of f(x) is getting zero. Because floating point numbers can’t be compared directly, we have to compare f'(x) against the smallest possible floating point number close to zero which we can get by calling std::numeric_limits<double>::min(). In such a case, where f'(x) is zero, the algorithm wouldn’t be able to converge (stationary point) as shown in the image below.

The advantage of the Newton method is its raw speed. In our case, it just needs 6 iterations until the algorithm reaches the convergence criteria of  . But the algorithm also has several drawbacks as implied above. Such as:
. But the algorithm also has several drawbacks as implied above. Such as:
- Only suitable if we know the derivative of a given function
- Only suitable for smooth and continuously functions
- If starting point
 is chosen wrong or the calculated point
is chosen wrong or the calculated point  at or close to a local maximum or minimum, the derivative of f'(x) gets 0 and we have a stationary point condition.
at or close to a local maximum or minimum, the derivative of f'(x) gets 0 and we have a stationary point condition. - If the derivative of a function is not well behaving, the Newton method tends to overshoot. Then
 might be way too far from root to be useful to the algorithm
might be way too far from root to be useful to the algorithm

Secant Method
In many cases, we don’t have, or it might be too complex, a derivative of a function f(x). In such cases, we can use the Secant method. This method basically does the same thing as the Newton method, but calculates the necessary slope not via its function derivative f'(x) but through the quotient of two x and y values calculated with f(x).


Implementation of Secant Algorithm
This algorithm needs a range [a,b] which might include (not absolutely necessary but it helps) the root we are searching for. It uses the method calculateX() which not only calculates  , but it also checks if the denominator
, but it also checks if the denominator  is
is 0. Also, this algorithm is very fast, it needs only 7 iterations in a well-chosen range and 10 iterations in a broader range. Both calculations fulfill the same convergence criteria of  . As well as the Newton method, this algorithm also has its drawbacks which we have to be aware of:
. As well as the Newton method, this algorithm also has its drawbacks which we have to be aware of:
- Only suitable for smooth and continuously functions
- If one of the calculated points
 at or close to a local maximum or minimum, the derivative of f'(x) gets 0 and we have a stationary point condition.
at or close to a local maximum or minimum, the derivative of f'(x) gets 0 and we have a stationary point condition. - If the calculated slope quotient of a function has a very low steepness, also the
Secant method tends to overshoot. Then  might be way too far from root to be useful to the algorithm.
might be way too far from root to be useful to the algorithm. - If the range [a,b] is chosen wrong, e.g., including local minimum and maximum, the algorithm tends to oscillation. In general, minimum and maximum, local or global, are in some cases a problem for the Secant method

Dekker Method
The idea of Dekker’s method is now to combine the speed of the Newton/Secant method with the convergence guarantee of Bisection. The algorithm is defined as the following:


 is the current iteration guess of the root and
is the current iteration guess of the root and  is the current counterpoint of
is the current counterpoint of  such that
such that  and
and  have opposite signs.
have opposite signs.- The algorithm has to fulfill the criteria
 such that
such that  is the closest solution to the root
is the closest solution to the root  is the last iteration value, starting with
is the last iteration value, starting with  at the beginning of the algorithm
at the beginning of the algorithm- If s is between m and
 then
then  , otherwise
, otherwise 
- If
 then
then  otherwise
otherwise 
Implementation of Dekker Algorithm
As we can see in the implementation of Dekker’s method, we always calculate both values, m and s, with the methods calculateSecant() and calculateBisection() and assign the results depending on what the method useSecantMethod() confirms if s is between m and  (as in rule 4 defined). In line 32-33, we confirm if the resulting values of the function f(x) fulfill rule number 5. Because of the
(as in rule 4 defined). In line 32-33, we confirm if the resulting values of the function f(x) fulfill rule number 5. Because of the Bisection, we have to check and correct after each iteration if the condition of $latex f(a_k)f(b_k) < 0 &s=1 & is still accomplished which is done with the method checkAndFixAlgorithmCriteria().

The Dekker algorithm is as fast as the Newton/Secant method but also guarantees convergence. It takes 7 iterations in case of a well-chosen range and 9 iterations in case of a broader range. As we can see, the Dekker algorithm is very fast but there are examples where  is extremely small but is still using the secant method. In such cases, the algorithm will take even more iterations as the pure
is extremely small but is still using the secant method. In such cases, the algorithm will take even more iterations as the pure Bisection would take.
Brent Method
Because of Dekker’s slow convergence problem, the method was extended by Brent which is now known as Brent’s method or Brent-Dekker-Method. This algorithm is extending Dekker’s algorithm by using four points (a, b,  and
and  ) instead of just three points, additional Inverse Quadratic Interpolation instead of just linear interpolation and Bisection, and additional conditions to prevent slow convergence. The algorithm decides with the following conditions which of the methods to use,
) instead of just three points, additional Inverse Quadratic Interpolation instead of just linear interpolation and Bisection, and additional conditions to prevent slow convergence. The algorithm decides with the following conditions which of the methods to use, Bisection, Secant method or Inverse Quadratic Interpolation:
- Bisection (B = last iteration was using Bisection)
- Inverse Quadratic Interpolation
- In all other cases use the
Secant method
Implementation of Brent Algorithm
With these modifications, the Brent algorithm is at least as fast as Bisection but in best cases slightly faster than using the pure Secant method. The Brent algorithm takes 6 iterations in case of a well-chosen range and 9 iterations in case of a broader range.

But Which Algorithm to Choose?
We have seen five different algorithms we can use to approximate the root of a function, Bisection, Newton method, Secant method, Dekker, and Brent. All of them have different possibilities and drawbacks. In general, we could argue which algorithm to use as the following:
- Use the
Newton method in case of smooth and well- behaving functions where you also have the function’s derivative - Use the
Secant method in case of smooth and well-behaving functions where you don’t have the function’s derivative - Use the
Brent method in cases where you’re not sure or know your functions have jumps or other problems.
| Algorithm | Start/Range | No. Of Iterations |
| Bisection | [0, 2] | 36 |
| Newton | x0 = 1.5 | 6 |
| Secant Good | [1.5, 2] | 7 |
| Secant Bad | [0, 2] | 10 |
| Dekker Good | [1.5, 2] | 7 |
| Dekker Bad | [0, 2] | 9 |
| Brent Good | [1.5, 2] | 6 |
| Brent Bad | [0, 2] | 9 |
Did you like the post?
What are your thoughts? Did you like the post?
Feel free to comment and share this post.
