Introduction
The code implements the Gauss Newton method for solving non linear least squares, applied to the Zener diode IZ(VZ) model.
Background
Recently, I was considering the unexpected effect of a Zener diode current absorption on the input stage (ADC) of a microcontroller; the Zener was just expected to clamp possible high voltages, not to alter noticeably the input signal, as it actually did. Unfortunately, the diode datasheet did not provide detailed information about the IZ(VZ), so I had to measure it and then, irremediably attracted by, try to model it.
This articles describes the process.
Disclaimers
- This article does NOT try to explain or even introduce the Gauss Newton algorithm (it is already well detailed on Wikipedia, for instance). It merely uses it for a purpose.
- Gauss Newton method is used because it fits nicely (pardon the pun). Though I am sure there are more advanced methods to compute not linear least squares, I simply don't care. I had fun coding it.
The Experimental Data
Experimental data was collected using the trivial circuit shown in Picture 1: an adjustable voltage generator (laboratory power supply) connected with the series of a 992 Ohm resistor and the 3V3 Zener diode. The voltage generator fed the circuit providing both forward and reverse voltage to the Zener.

Picture 1: Circuit showing the measurement points.
In such a circuit, the same current flows in the resistor and the Zener:
IZ = IR = VR/R
So, measuring VZ and VR, all the needed data would be obtained.
However the additional measure of VTOT is not just a waste of (my) time, because it provides a 'redundancy check' of the collected {VZ, IZ} pair.
The Data File
There have been collected 123 data points, with VTOT ranging from about -21 V to (about) 18 V.
The corresponding values are available in the data.csv file. Picture 2 shows a partial view of the data.

Picture 2: Partial view of the collected data.
The Experimental Curve
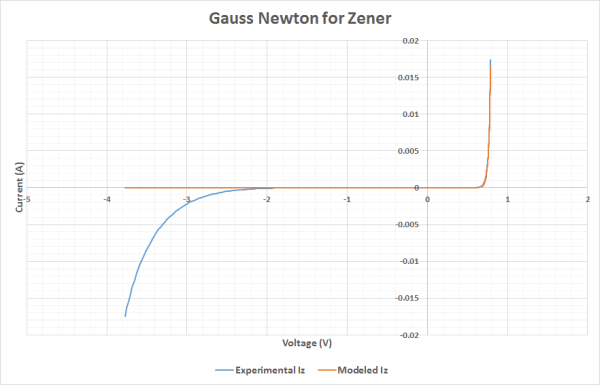
Collected data is represented by the curve plotted in Picture 3.

Picture 2: The experimental data points.
The characteristic behaviour of the Zener is shown: exponential current raise at forward voltage (about 0.7 V in this case), exponential raise, with a very different, more gently slope, of (negative) current at reverse breakdown voltage (about the nominal -3.3 V).
In the middle zone, the current is very low.
The Model
The IZ(VZ) model chosen is the 'exponential diode'.

In this article, I consider only the equation (1) which should be valid only in the V > -VB range, where VB is the (Zener) diode 'Breakdown Voltage'.
Picture 0, at the top of the page, in effect shows such equation spectularly failing in the invalid range ( V <= -VB).
Since the Zener is a 3V3 one, its nominal VB is 3.3 V. The aim of this test, however, is to establish experimentally the range of validity of the equation (1).
The Plan
The plan consists in iteratively applying the Gauss Newton method (not linear least squares) to a subrange (tail) of experimental data until a satisfying fit is achieved, in order to establish the 'Experimental Breakdown Voltage' (VBE) of the Zener diode.
(Such a result will be the starting point for another article, in which a fit for the equation (2) in the V < -VBE range has to be found).
The Details
- In step 0, all the experimental data are considered for fitting the model (VStart = Vmin = V0). the corresponding variance is computed.
- In step 1, the first experimental point is excluded (VStart = V1), fitting is applied to remaining tail of data, the corresponding variance is computed.
- In step 2, both the first and second experimental point are excluded (VStart = V2), the fit is applied and the variance computed on the remaining tail of data.
- ...
- In step 83, stop it all, because now the tail of data is pretty small.
Finally, the graph of variance(Vstart) is plotted in order to estimate VBE.
The Gauss Newton Algorithm
The Gauss Newton algorithm is an iterative method for solving not linear least squares (details at the very Wikipedia page: Gauss–Newton algorithm[^]).
The iteration step n+1, that is the value of the estimated parameters of the model at step n+1 is:

In our case, after rewriting the equation (1) this way:

We have the model function:

And the iteration step components:

Where the vectorial nature of the parameters (2 components) and residual (N components) is shown explicitly, likewise the matrix nature (N x 2 elements) of the Jacobian.
Luckily, the product JTJ is a 2x2 matrix: its inverse computation is trivial.
The Code
The code is in a single source file gn2.cpp - it is compiled with g++-7, though any modern C++ compiler should do the trick.
It contains a single class, having the very original name GN, which is constructed (in main function) with all experimental data values (and the initial estimate of the parameters).
The main first sets, quite arbitrarily, 20 iteration steps, then calls the GN::compute method iteratively on the tail of data defined by the offset parameter:
for ( size_t offset = 0; offset <= (N - 40); ++offset)
{
cout << "----------------------\n";
cout << "starting with item:\n" << offset << endl << endl;
auto [ best_pe, best_var] = gn.compute(steps, offset);
cout << "best pe:\n" << best_pe << endl;
cout << "best variance:\n" << best_var << endl << endl;
}
cout << "done." << endl << endl;
For every range is reported:
- on the standard output, the best computed variance, together with the corresponding estimate of parameters.
- on a log file, named
gn_<offset>.log (e.g. gn_009.log) all the clerical details of the computation (yes, roughly 80 log files are generated :-) ).
Excerpt of console output:
...
----------------------
starting with item:
9
best pe:
2.10572e-17
43.5169
best variance:
0.000195843
...
Excerpt of the corresponding log file gn_009.log:
experimental data
ex:
-3.773
-3.753
[...]
ey:
-0.0174294
-0.0164012
[...]
parameter estimates starting value
epe
5.18e-20
51.2
####################
step 0
r:
0
0
[...]
variance:
0.000197485
j:
0 0
0 0
[...]
jt:
0 0 0 0 [...]
[...]
jtr:
6.88719e+13
1.81736e-06
jtj:
7.32544e+35 2.96725e+16
2.96725e+16 0.00120204
inv_jtj:
1.30385e-32 -3.21856e-13
-3.21856e-13 7.94587e+06
identity:
1 0
0 1
dpe:
3.13055e-19
-7.72628
new parameter estimates:
3.64855e-19
43.4737
[...]
Where identity = (JTJ)-1 · (JTJ) is a 'consistence check', while dpe is the increment (delta) on the parameter estimates.
The Variance Graph
Variances computed for different ranges have been collected and plotted on a graph:

Picture 3: Variance of the fit computed on different ranges of experimental data.
The graph confirms once again the unsuitability of the equation (1) for voltages V < -VB.
It additionally indicates the experimental value VBE of the breakdown voltage. As a matter of fact, the model 'behaves well' when:
V > -VBE ≅ -2.8 V
Points of Interest
I use std::vector everywhere, every time, but, in this particular application, I discovered that the std::array, coupled with templates provides a powerful and neat tool for matrix computation, for instance, consider:
template <size_t R, size_t C>
array< array < double, R>, C > transpose
( const array < array< double, C >, R > & m, size_t offset)
{
array< array < double, R >, C > t{0}; for (size_t r = offset; r<R; ++r)
for ( size_t c = 0; c < C; ++c)
t[c][r] = m[r][c];
return t;
}
It is, in my opinion, an almost self-documenting implementation of the transpose operation.
You could achieve a neater implementation discarding the offset parameter, which I used here in order to gain performance at the expense of generality.
History
- 30th June, 2019 - First release
