License: MIT
Author: Anthony Daniels
Abstract
A new Open Source general purpose Data Sorting Engine that uses Fuzzy Logic Model based sorting is described. Unlike traditional sorting methods which sort nested columns of data (e.g., sort on A increasing, then B decreasing, then C increasing…), FuzzySortLib transforms the sorting problem into a Multi-Objective Optimization problem and sorts the results of the model. Unlike traditional multi-objective methods, the proposed method transforms the problem into a Fuzzy Programming equivalent similar to that outlined in Reference [1]. The Fuzzy Programming Model is applied to the data and the results are then sorted.
Index Terms—Data Sorting, Fuzzy Logic, Fuzzy Programming, Multi-Objective Optimization, Open Source, Sorting Engine
Introduction
In today’s world of search engine results, online shopping, and big data, sorting data happens on a continuous basis. When sorting these data sets the standard typically users use a nested sort where the data is sorted on one variable then the next until the end of the nesting. However, this type of sorting doesn’t handle the scenario where the user wants all columns considered together as a whole. In that scenario, the nested sorting method breaks down. Consider shopping for cars as an example. This example will be used throughout the article. When looking at cars, there are many independent variables to consider (e.g., Horsepower, Number of Seats, Trim Options, Cargo Capacity, MPG, etc.). The user has preferences to all of these and what they really want is to look at the data as a whole, satisfying as many of the individual variables as possible. What you really have is a multi-objective optimization problem where all of the independent variables represent individual objectives or constraints. The goal is to sort the data based on which row of data most satisfies all of the independent objectives or constraints. That is where formulating the data sorting problem as a Fuzzy Programming problem is beneficial. The following section is an excerpt from Reference [1] which explains Fuzzy Programming and how it relates to the data sorting problem.
Fuzzy Programming
Fuzzy Programming, as a method of optimization, takes the existing mathematical formulation of the objectives and constraints and transforms them into fuzzy preference functions [3]. This is best shown by example. As an illustration, take the simple constraint of X1 <= 5. Transformed, the constraint looks like the fuzzy utility preference function in Figure 1. Less than or equal to 5, the fuzzy constraint is fully satisfied with a utility of 1.0. This decreases as the constraint is violated until it maintains an unsatisfied value of 0.05. In fuzzy utilities, the fully unsatisfied constraint is a non-zero small number. The reason for this is that 0 utility means fully infeasible. Unfortunately, set operations with fully infeasible values lose all information in the multiplicative set inferences and thus make decision engines for agents ineffective at improving solutions that are temporarily in infeasible regions of the search space.
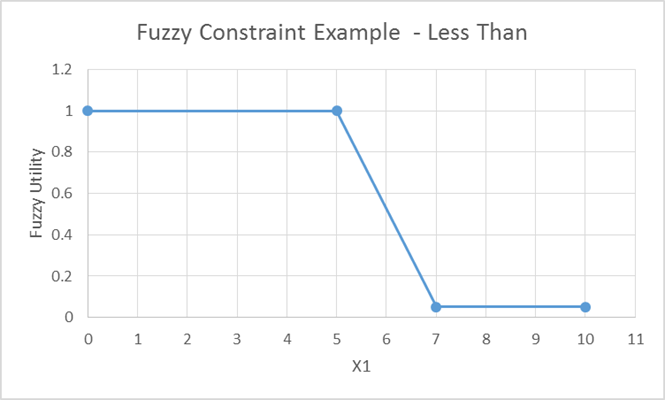
Figure 1: Example Fuzzy Constraint – Less Than or Equal to
Similarly to constraints, objective functions can also be turned into fuzzy utility functions. This is done through a process where the Pareto set current lower bound and upper bound are converted into a linear fuzzy utility preference function. This again is best illustrated by example. Say we have the objective function max f(x) = x1 + x2^2 and the current Pareto Set of candidate solutions has an objective function value range of [4.3…15.7], then the fuzzy utility would look like Figure 2.

Figure 2: Example Fuzzy Objective Function – Maximize F(x)
Extending this to multi-objective optimization is as simple as performing set operations on the fuzzified objective functions. For example:

Fi(x) is the fuzzy utility function of fi(x) and MIN is the minimum set operator. We are maximizing the minimum of the fuzzy utility functions. In terms of fuzzy set mathematics, this is the same as the AND operator. The proposed system performs the MIN and AVG operators on the set of fuzzy objective functions. This differs from weighted sum multi-objective methods that use scaling factors with summation, and not set operations to combine and reduce the number of objective functions.

Using the set operator in (4) provides upward pressure on both the min and the average of the objective utilities. This can be useful in scenarios where there is an unhappy objective function that is never satisfied. The average operator provides pressure on the group as a whole. Similarly, the same operator is applied to the set of constraints to roll up the collection into a single constraint utility. By using Fuzzy Programming, the sorting problem allows the user to compare rows of data based on a Multi-Objective Optimization approach looking at the data as a whole instead of a traditional nested sort which looks only at individual variables one at a time.
Fuzzy Sorting
The Fuzzy Sorting problem is essentially a Constraint Programming problem. Each individual variable is assigned a Fuzzy Preference Function representing the user’s satisfaction over the range of values. All of the constraints are then pooled together into a single objective via the Min-Average set operator outlined in the previous section. The data is then sorted on that single objective function value.
Using our car example, we have the following variables to consider and their desired preference functions.
- Price -> Minimize
- MPG -> Maximize
- Cylinders -> Polyline Preference Function
- Engine Size -> Maximize
- HorsePower -> Maximize
- Torque -> Greater Than
- Seating -> Goal Seek
- Warranty Years -> Greater Than
- Warranty Miles -> Equal To
- Length -> Minimize
- Cargo Capacity -> Maximize
As can be seen by the above variables, there can be a mix of different constraint types. The FuzzySortLib supports the following constraint types:
- Double Gaussian
- Polyline
- Goal Seek
- Minimize
- Maximize
- Lookup Map (for string value or enumerated variables)
- Less Than
- Greater Than
- Equal To
- Not Equal To
Any of the constraint types can be used for an individual variable. That is the power of Fuzzy Programming. You can mix types freely. Below is a figure with the various Constraint types and their preference curves for illustration. In the case of the cars, we are comparing them across ALL variables at the same time and sorting accordingly. The results of the provided car model are shown below.
Theory Section Conclusion
Fuzzy Sorting provides a powerful Multi-Objective Optimization approach to sorting data. By looking at the sorting problem as a constraint programming problem, we are able to sort data based on all of their independent variables simultaneously. In the example of the cars, we were able to sort the data finding the car that best fits our collective desired preferences. Future work with this library will introduce weights to the individual constraints allowing for relative importance comparison between independent variables.
FuzzySortLib Code Manual
FuzzySortLib is a relatively compact library. There are the following classes:
FSLibModel – the main fuzzy programming model that evaluates a collection of contstraintsFSLibConstraint – the fuzzy programing preference function for an individual variable. It can be of the forms outlined in the previous section. Each different constraint type has different inputs. More on constraint types will be discussed in the next section.
- Double Gaussian Inputs – Left Mean, Left Sigma, Right Mean, Right Sigma
- Polyline Inputs - Left Mean, Right Mean, PolylinePoints
- Goal Seek – Seek Value, Current Min, Current Max
- Minimize Inputs - Current Min, Current Max
- Maximize Inputs - Current Min, Current Max
- Lookup Map Inputs – <String, Preference> Map Entries
- Less Than Inputs– Preference, Threshold
- Greater Than Inputs – Preference, Threshold
- Equal To – Preference, Delta
- Not Equal To Inputs – Preference, Threshold
FSLibVariable – the variant type independent variable. It can represent both floating point and string data.FSLibUtilPoint – the basic xyz data point used in polyline preference functions.
Evaluating a model to a data set requires that the model has been created with the model editor (next section) or programmatically. The model is loaded, then the data set is loaded. It is important to note that the model and the data columns have to be in the same order. It is also important to note that the data has to have the first column be the row name variable. This can be either number or string but they have to be unique. In the car example, it is the name of the car type. Evaluating a model can be done with the following code from QtFSLib_ModelData_Evaluator.cpp:
int numRows = m_arrRawData.size();
int numCols = m_arrHeaders.size();
std::vector<double> arrMinVal, arrMaxVal;
for (int n = 0; n < numCols; n++)
{
arrMinVal.push_back(m_arrRawData.at(0).at(n).m_dblVar);
arrMaxVal.push_back(m_arrRawData.at(0).at(n).m_dblVar);
}
for (int m = 0; m < numRows; m++)
{
for (int n = 0; n < numCols; n++)
{
double dblTemp = m_arrRawData.at(m).at(n).m_dblVar;
if (dblTemp < arrMinVal.at(n))
{
arrMinVal.at(n) = dblTemp;
}
if (dblTemp > arrMaxVal.at(n))
{
arrMaxVal.at(n) = dblTemp;
}
}
}
if (m_ptrModel->CountConstraints() != (numCols - 1)){ return; }for (int n = 1; n < numCols; n++)
{
m_ptrModel->AtConstraint(n - 1).Set_dblCurrMin(arrMinVal.at(n));
m_ptrModel->AtConstraint(n - 1).Set_dblCurrMax(arrMaxVal.at(n));
};
std::vector<ModelDataRow> AllRows;
double dblOverallMinUtil = 1.0f;
double dblOverallMaxUtil = 0.0f;
for (int m = 0; m < numRows; m++)
{
ModelDataRow tempRow;
tempRow.m_dblOverallUtil = 0.0f;
tempRow.m_strName = m_arrRawData.at(m).at(0).m_strVar;
for (int n = 1; n < numCols; n++)
{
tempRow.m_arrConstUtils.push_back(m_arrRawData.at(m).at(n));
}
tempRow.m_dblOverallUtil = m_ptrModel->EvaluateModel(tempRow.m_arrConstUtils);
if (tempRow.m_dblOverallUtil < dblOverallMinUtil)
{
dblOverallMinUtil = tempRow.m_dblOverallUtil;
}
if (tempRow.m_dblOverallUtil > dblOverallMaxUtil)
{
dblOverallMaxUtil = tempRow.m_dblOverallUtil;
}
AllRows.push_back(tempRow);
}
std::sort(AllRows.begin(), AllRows.end(), SortDataDescending);
FuzzySortLib Model Editor and Evaluator
For tutorial and ease of use reason, a QT based model editor has been provided for both creating FSLibModels and applying that model to data. This is what the main user interface looks like:

This is a typical use case for the editor. Create a New FSLibModel by selecting the File->New Model menu item. A new model with three constraints will be created. Click Add or Remove Constraints to get the desired number of constraints for your model. Remember that order between the model and data set has to be consistent throughout the process. For each constraint, select the constraint in the list view on the left. Then select what type of constraint you want that variable to be. The appropriate editor will appear on the right. Make sure you change the name to the variable header in your column data. Edit the settings for the constraint, then Click the Save Constraint button to persist your changes. Do this for every constraint and when you are done, save your model using the File->Save Model menu item. The file type for FSLibModels is an .xml file.

You can load an already created model by using the File->Open Model menu item. Once your model is loaded and you are ready to work with data, select the Analysis->Show Model Data menu item. Then select the Analysis->Open Model Data menu item to load the .csv file of your data. Remember that the first column has to be the name and the order of the data has to match the order of your model constraints. When you are ready to run the model data, select the Analysis->Run Model menu item. Your fuzzy sorted data should show up in the results table. If you want to copy the results for export, click the Copy All Data button. Your data is now sorted using the fuzzy sorting model.

References
History
- 28th August, 2019: Initial version
