This article discusses the process of building and exporting an AI deep learning TensorFlow model used for S&P 500 Index indicator values prediction.
Introduction
This is the second article in the series, in which we will discuss about the process of building and exporting an AI deep learning TensorFlow model used for S&P 500 Index indicator values prediction:
"The S&P 500, or just the S&P, is a stock market index that measures the stock performance of 500 large companies listed on stock exchanges in the United States. It is one of the most commonly followed equity indices, and many consider it to be one of the best representations of the U.S. stock market. The average annual total return of the index, including dividends, since inception in 1926 is 9.8%; however, there were several years where the index declined over 30%. The index has posted annual increases 70% of the time." - Wikipedia - S&P 500 Index.
The S&P 500 Index indicator values prediction is a very common example widely used for deploying and testing various of AI deep learning models and solutions that perform a univariete time series prediction.
The building and exporting the S&P 500 Index indicator values using TensorFlow is a very essential phase of the SAP-HANA based solution development cycle, discussed in this series of articles.
The audience of this article's readers will find out how to deploy an AI deep learning model used for S&P 500 Index prediction. The entire material of this article includes the following essential topics, such as the data importing, preparation and normalization phase, designing the model architecture and its implementation using TensorFlow library, exporting and saving model on disk in the TensorFlow Model Server format.
Import and Prepare S&P 500 Index Dataset
Before building and exporting S&P 500 Index prediction model using TensorFlow, let’s first take a look at the data we’re about to use for our model’s training. For that purpose, we will use a fragment of the dataset, prepared by Sebastien Heinz at STATSWORKS and published in his article "A simple deep learning model for stock price prediction using TensorFlow" at Medium.
The following intraday dataset, stored in CSV-format, contains minute data on the stock prices of top S&P 500 constituent American companies (i.e., “tickers”), that is associated with a specific S&P 500 indicator value:
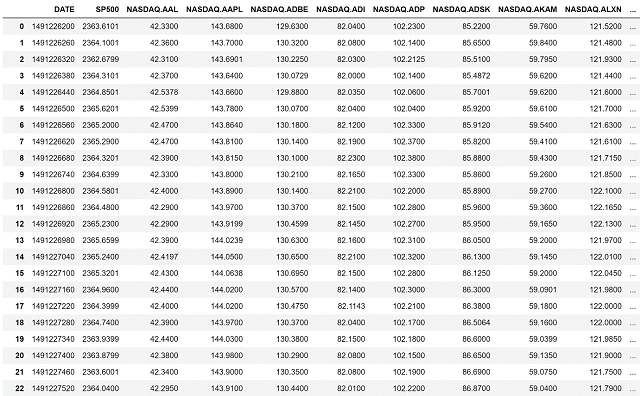
The following dataset structure is very simple. The first column of the following micro-dataset is a timestamp in Unix-format, representing the moments of time, at which the specific stocks prices are updated. The second column “SP500” contains the actual values of the S&P 500 Index updated at each moment of time (e.g., every 60 seconds). The real-time values of stock prices for each of S&P 500 companies are stored in the rest of other 500 columns (e.g., NASDAQ.AAL, NASDAQ.AAPL, NASDAQ.ADBE, …), as shown in the figure above.
Obviously, that, the following dataset is ideal for building a specific deep learning model, since it contains enough data used for the deep learning model training, providing a high-quality prediction. Specifically, the entire dataset contains almost 2 x 10^3 minutes of data, starting April 2017. Moreover, the other existing datasets contain much less data, such as 20 or 50 company tickers values, whilst the following dataset contains a complete number of stocks pricing values for each S&P 500 ticker (e.g., N = 500), that will further be used for fitting our prediction model.
As you’ve already noticed, the pricing values for each particular moment of time are almost the same and slow to variate. This actually means that we basically deal with a univariate dataset. The using of univariate datasets for deep learning model training purposes actually requires a specific dataset normalization.
At this point, let’s discuss how to prepare the following dataset for the S&P 500 Index prediction model training and testing purposes. To be able to use the following data for fitting the prediction model being created, we must split up the entire dataset discussed above into two specific datasets, one for training and one for testing our model. Also, each of these datasets must consist of two essential sets of either model’s input or output data, respectively. According to the structure of the entire dataset stored in CSV-format, the values of all those 500 columns, representing each company’s stock prices, will be used as an input and all values in the second “SP500” column, representing the current S&P 500 indicator value, – as the output of the learning model being created.
To load the dataset stored in CSV-format, we will use the Pandas library, providing the capability of processing the CSV-data in our Python script. To load the CSV-data file, we will implement the following code:
dataset = pd.read_csv(filename).values.tolist()
The following line of code loads the file into the Pandas data frame dynamically and then converts the current data frame into Python’s generic list.
After converting the specific data from the Pandas data frame into Python’s list, we must slice the entire dataset horizontally by using the code listed below.
First, we have to compute the actual shape of the 2D-list we’ve previously obtained. To do that, we need to convert the list into a Python’s NumPy array and get the number of items for each dimension by using the following code:
shape_x = np.array(dataset).shape[0]
shape_y = np.array(dataset).shape[1]
Then, we have to slice the array by using Python’s array-wise operators, such as:
x_set = np.array(dataset)[:,2:shape_y + 2]
y_set = np.array(dataset)[:,1]
At the end of performing the following computations, we will obtain two arrays x_set and y_set. The first array x_set contains each row values for all of 500 columns stored in the original dataset, and the second y_set array will contain values from each row of the second “SP500” column only. Obviously, that, the first array x_set consists of the data used as an input dataset, and the second array – the output dataset of the model being created.
After that, our goal is to produce two subsets of data used for either training or testing purposes, respectively. This is typically done by using the following Python code:
train_start = 0
train_end = train_start + int(shape_x * ratio)
test_start = train_end + 1
test_end = len(dataset)
train_X = x_set[train_start:train_end:]
train_Y = y_set[train_start:train_end:]
test_X = x_set[test_start:test_end:]
test_Y = y_set[test_start:test_end:]
The main principle of this code shown below is that we must first compute the starting and ending position of either training or testing datasets in the x_set and y_set array and then slice them vertically to obtain those training and testing datasets. According to the best practices, we will use the ratio training set size value. At this point, all that we have to do is to declare the train_start variable and initialize it with the value of 0. In this case, the train_start variable will be assigned to the training dataset starting position index. Similarly, we must declare another variable train_end and compute the training dataset ending position by multiplying the overall number of rows in the array by a certain ratio value (for example, train_ratio = 0.5, which means that we want 50% of rows to be stored in the training dataset). After that, we can compute the starting and ending position of the testing dataset by declaring another two variables such as test_start and test_end. The first variable test_start is assigned to a value of the training dataset ending position train_end incremented by 1, and the second variable test_end is assigned to the value of the last row index in the array.
After computing those ranges, we can now easily slice the data to obtain the x_set and y_set arrays, respectively. To do that, we must use the Python’s array-wise operators, as it’s shown in the code listing above.
Data Normalization
Prior to using those input and output datasets, the specific data must be properly normalized. This is typically done to prevent the case in which our model is overfitted, which, in turn, makes the model training process to be inefficient.
The easiest way to normalize the data is to use the Min-Max scaling method. The following method allows scaling each value, representing it in the interval [0;1]. There are also other similar methods such as Standard scaling that uses Standard Deviation Value (STD), but, in this case, the Min-Max scaling should be enough to properly normalize those data used for S&P 500 Index prediction.
To normalize the data using the Min-Max scaling method, we use the following formula applied to each pricing value:
$\begin{aligned}X_{norm}=\frac{X - X_{min}}{X_{max} - X_{min}}\end{aligned}$
where
$\begin{aligned}X\end{aligned}$
is unnormalized raw pricing value,
$\begin{aligned}X_{min}\end{aligned}$
is the minimum pricing value for a current column,
$\begin{aligned}X_{max}\end{aligned}$
is the maximum pricing value for a current column,
$\begin{aligned}X_{norm}\end{aligned}$
is the normalized pricing value in the interval [0;1];
To denormalize those data, we must use the following formula:
$\begin{aligned}X = X_{norm} \times (X_{max} - X_{min}) + X_{min}\end{aligned}$
where $\begin{aligned}X\end{aligned}$
is denormalized pricing value,
$\begin{aligned}X_{min}\end{aligned}$
is the minimum pricing value for a current column,
$\begin{aligned}X_{max}\end{aligned}$
is the maximum pricing value for a current column,
$\begin{aligned}X_{norm}\end{aligned}$
is normalized pricing value in the interval [0;1];
To perform such normalization/denormalization, we must implement these two Python procedures:
def normalize(dataset):
if len(np.array(dataset).shape) > 1:
min_vals = np.array(dataset).min(axis=0)
max_vals = np.array(dataset).max(axis=0)
for col in range(0, len(dataset[0])):
for row in range(0, len(dataset)):
if (max_vals[col] - min_vals[col]) != 0.0:
dataset[row][col] -=min_vals[col]
dataset[row][col] /= (max_vals[col] - min_vals[col])
else: dataset[row][col] = 1.0
return (dataset, min_vals, max_vals)
else:
min_val = np.array(dataset).min()
max_val = np.array(dataset).max()
for index in range(0, len(dataset)):
if (max_val - min_val) != 0.0:
dataset[index] -= min_val
dataset[index] /= (max_val - min_val)
else: dataset[index] = 1.0
return (dataset, [min_val], [max_val])
def denormalize(dataset, min_vals, max_vals):
if len(np.array(dataset).shape) > 1:
for col in range(0, len(dataset[0])):
for row in range(0, len(dataset)):
if (max_vals[col] - min_vals[col]) != 0.0:
dataset[row][col] *= (max_vals[col] - min_vals[col])
dataset[row][col] += min_vals[col]
else: dataset[row][col] = min_vals[col]
else:
for index in range(0, len(dataset)):
if (max_vals[0] - min_vals[0]) != 0.0:
dataset[index] *= (max_vals[0] - min_vals[0])
dataset[index] += min_vals[0]
else: dataset[index] = min_vals[0]
return dataset
The first function normalize(dataset) accepts a single argument of the dataset being normalized. While performing the normalization, the following function finds either minimum or maximum values for each column, and, then loops over each value in the current column applying the Min-Max scaling formula listed above. In case all values in the current column are equal, it replaces each value with a value of 1.0.
The second function denormalize(dataset, min_vals, max_vals) listed above performs almost the same, but accepts three arguments such as a dataset, an array of columns’ minimum values and an array of maximum values, respectively. Then, it uses these min and max values to denormalize each value in each column by applying the second denormalization formula to each value.
According to the best practices, I’ve implemented normalization and denormalization function that can normalize/denormalize either 1D and 2D-arrays. To find the minimum and maximum values for each column, I’ve used already implemented methods of Python’s NumPy library. Here’s the code that illustrates how these normalization functions are used:
(train_X, train_min_vals_X, train_max_vals_X) = normalize(train_X)
(train_Y, train_min_vals_Y, train_max_vals_Y) = normalize(train_Y)
(test_X, test_min_vals_X, test_max_vals_X) = normalize(test_X)
(test_Y, test_min_vals_Y, test_max_vals_Y) = normalize(test_Y)
After performing the normalization, our dataset will look as follows:
array([[0.87724435, 0.24034211, 0.2995815 , ..., 0.3976612 , 0.8962966 ,
0.9130416 ],
[0.8947885 , 0.24892762, 0.5907224 , ..., 0.32748637, 0.8111101 ,
0.9130416 ],
[0.8655475 , 0.24467744, 0.55063736, ..., 0.33333334, 0.78518426,
0.92608786],
...,
[0.8246096 , 0.18455261, 0.28270024, ..., 0.7076022 , 0.21851741,
0.37826157],
[0.80706316, 0.18455261, 0.29535797, ..., 0.7309945 , 0.21851741,
0.36521864],
[0.80706316, 0.18455261, 0.27848312, ..., 0.72514534, 0.22592641,
0.3739128 ]], dtype=float32)
As you can see from the output above, each value of the normalized dataset resides in the interval [0;1]. Also, I’ve decided not to use any of the existing scaler objects such as MinMaxScaler or StandardScaler from Python’s Sklearn library, since it’s not possible to save those scaler objects into the model, built and exported.
Build RNN-Based TensorFlow Prediction Model
At this point, let’s take a look into the S&P 500 Index prediction model architecture and its implementation using the TensorFlow Keras library for Python. Obviously, that, we will use the sequential model to build up a model that can be used for predicting S&P 500 Index indicator values.
Before designing the model, let’s get back and see what data is passed to the inputs and outputs of the model during the training process. As we’ve already discussed, we sliced the entire dataset grid into a tuple of 2D-arrays containing either input or output data. Obviously, that, each training sample is 1D-array and doesn’t require to be reshaped.
The input dataset is actually a 2D-array each row of which is a training sample containing values from 500 tickers, passed to the inputs of each neuron in the model’s input layer.
The output dataset is also a 2D-array each row of which contains a single S&P 500 Index value passed to the output of the model, during the training process.
In this case, we will use the TensorFlow’s Dense layers as the first input and the last output layers of the model being created.
To improve the quality of prediction and drastically reduce the amounts of data required for training, we will use the Recurrent Neural Network (RNN) with Gateway Recurrent Unit (GRU) cells as a hidden layer of the entire model designed. Specifically, we will interconnect dense input and output layers with the RNN-based hidden layer via both the Reshape and Flatten TensorFlow layers, respectively. The entire structure of the model being designed is shown in the figure below:

According to the architecture of the following model, the first dense layer has the input dimension of 500 values. It actually means that each neuron in the input layer will have 500 inputs. For prediction purposes, we will design the input dense layer consisting of N1 = 100 neurons that should be quite enough for providing the desired quality of prediction. Next, the following input layer is interconnected with the reshape layer, in which the input layer’s output data is reshaped into a 2D-array of the RNN’s inputs. The requirement of using RNNs is that an input array must have the following 3D-shape: [samples, timesteps, features]. Specifically, we will represent the flat array of input layer’s outputs as a shape, in which samples = 10, timesteps = 10, features = 1 (e.g. [10, 10, 1]), and pass it to the RNN’s inputs. To implement an RNN-based hidden layer, we will create a generic list of GRU-cells, each one containing 8 units and uses the ReLU activation function, which is perfect for the univariate time series prediction.
Finally, we have to interconnect the RNN layer with the output dense layer. As we’ve already noticed, the RNN being used typically has the same output shape as its input, which normally conflicts with the one-dimensional input shape of the output dense layer. As a workaround to this problem, we must use the TensorFlow Flatten layer to reshape the RNN’s outputs into a flat 1D-array passed to the inputs of the last output dense layer.
Since the following model is being designed to predict a single value of the S&P500 Index, the output dense layer consists of a neuron, having 8 inputs and only one output.
To provide the desired quality of prediction, for the model being designed, we will use Adam optimizer with learning rate Lr = 0.002. As well, we will use the mean-squared-error loss function that is commonly used for time series prediction.
The Python code implementing the following model using Keras library is listed below:
model = tf.compat.v1.keras.Sequential()
model.add(tf.compat.v1.keras.layers.Dense(
tf_neurons_input_layer, input_dim=train_X.shape[1]))
model.add(tf.compat.v1.keras.layers.Reshape((int(tf_neurons_input_layer / 10),
int(tf_neurons_input_layer / 10)), input_shape=(tf_neurons_input_layer,)))
tf_gru_cells = []
for tf_gru_layer_ii in range(tf_gru_layers):
tf_gru_cells.append(tf.compat.v1.keras.layers.GRUCell(
tf_neurons_per_gru_layer, activation='relu'))
model.add(tf.compat.v1.keras.layers.RNN(tf_gru_cells,
return_sequences=True, input_shape=(
int(tf_neurons_input_layer / 10), int(tf_neurons_input_layer / 10))))
model.add(tf.compat.v1.keras.layers.Flatten())
model.add(tf.compat.v1.keras.layers.Dense(1, input_dim=tf_neurons_per_gru_layer))
Optimizer = tf.compat.v1.keras.optimizers.Adam(lr=0.002, beta_1=0.9,
beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)
model.compile(optimizer=Optimizer, loss='mse')
In this code, we first instantiate the sequential model and add the model’s first dense input layer along with the reshape layer. After that, we create a generic list of GRU-cells and pass it as an argument of RNN layer. Then, we add the flatten and output dense layer. Also, we must instantiate an optimizer object, passing the learning rate and other parameter values to its constructor. Finally, we must compile the model being created by invoking the specific compile(optimizer=Optimizer, loss=’mse’) method.
After the model has been successfully created, we can fit the following model by invoking the following method:
model.fit(train_X, train_Y, epochs=tf_epochs)
We normally pass the normalized input training datasets train_X and train_Y as the first and second arguments of this method. Also, we must specify the number of training epochs as the last argument of this method.
This method while being executed provides the following output:
Epoch 1/20
1599/1599 [==============================] - 1s 878us/sample - loss: 0.0127
Epoch 2/20
1599/1599 [==============================] - 1s 337us/sample - loss: 6.4495e-04
Epoch 3/20
1599/1599 [==============================] - 1s 336us/sample - loss: 6.0796e-04
Epoch 4/20
1599/1599 [==============================] - 1s 339us/sample - loss: 4.8388e-04
Epoch 5/20
1599/1599 [==============================] - 1s 340us/sample - loss: 5.3904e-04
Epoch 6/20
1599/1599 [==============================] - 1s 339us/sample - loss: 5.1811e-04
Epoch 7/20
1599/1599 [==============================] - 1s 340us/sample - loss: 4.5971e-04
Epoch 8/20
1599/1599 [==============================] - 1s 343us/sample - loss: 3.9597e-04
Epoch 9/20
1599/1599 [==============================] - 1s 338us/sample - loss: 4.8107e-04
Epoch 10/20
1599/1599 [==============================] - 1s 336us/sample - loss: 4.1709e-04
Epoch 11/20
1599/1599 [==============================] - 1s 340us/sample - loss: 3.7280e-04
Epoch 12/20
1599/1599 [==============================] - 1s 338us/sample - loss: 4.3241e-04
Epoch 13/20
1599/1599 [==============================] - 1s 340us/sample - loss: 3.8231e-04
Epoch 14/20
1599/1599 [==============================] - 1s 338us/sample - loss: 4.1684e-04
Epoch 15/20
1599/1599 [==============================] - 1s 337us/sample - loss: 4.0849e-04
Epoch 16/20
1599/1599 [==============================] - 1s 339us/sample - loss: 4.2306e-04
Epoch 17/20
1599/1599 [==============================] - 1s 338us/sample - loss: 4.1383e-04
Epoch 18/20
1599/1599 [==============================] - 1s 340us/sample - loss: 3.9852e-04
Epoch 19/20
1599/1599 [==============================] - 1s 338us/sample - loss: 4.0887e-04
Epoch 20/20
1599/1599 [==============================] - 1s 346us/sample - loss: 3.9221e-04
As you can see from the output above, the value of loss function is drastically decreasing after each model fitting epoch.
Finally, we must evaluate the model using the dataset previously created. To do that, we must invoke the following method, passing the evaluation dataset test_X as a single argument of this method:
predicted = model.predict(test_X, steps=1)
The following method returns an array of predicted S&P 500 Index values assigned to the predicted variable.
After that, we must denormalize those predicted values by invoking the following two methods:
test_Y = denormalize(test_Y, test_min_vals_Y, test_max_vals_Y)
predicted = denormalize(predicted, test_min_vals_Y, test_max_vals_Y)
To check if our model predicts the correct S&P 500 Index values, let's visualize the prediction results along with the target values of our evaluation dataset stored in test_Y array, obtained during the data preparation phase. To do that, we will use the Python's the matplotlib.pyplot library and invoke the following three methods to plot a specific chart and save it in jpg-format:
plt.plot(np.array(test_Y), color='blue')
plt.plot(np.array(predicted), color='red')
plt.savefig("5229100/sp500_result.jpg", dpi=None, facecolor='w', edgecolor='w',
orientation='portrait', papertype=None, format=None,
transparent=False, bbox_inches=None, pad_inches=0.1, metadata=None)
The following methods execution will create the following chart shown in the figure below:
As you can see from the chart above, both, the real and predicted S&P 500 Index indicator values are almost identical, which means that our model tends to provide the desired quality of prediction.
Export the Prediction Model
Since, we’ve successfully built and tested the prediction model, it’s time to discuss how to export this model and serve it using TensorFlow Model Server. To do this, we must implement the following Python code:
sess = tf.compat.v1.Session()
sess.run(tf.compat.v1.global_variables_initializer())
tf.compat.v1.keras.backend.set_session(sess)
tf.compat.v1.keras.backend.set_learning_phase(0)
builder = tf.compat.v1.saved_model.builder.SavedModelBuilder(path)
tensor_info_input = tf.compat.v1.saved_model.utils.build_tensor_info(model.input)
tensor_info_output = tf.compat.v1.saved_model.utils.build_tensor_info(model.outputs[0])
prediction_signature = (
tf.compat.v1.saved_model.signature_def_utils.build_signature_def(
inputs={'TICKERS': tensor_info_input},
outputs={'SP500INDEX': tensor_info_output},
method_name=tf.compat.v1.saved_model.signature_constants.PREDICT_METHOD_NAME))
builder.add_meta_graph_and_variables(
sess, [tf.compat.v1.saved_model.tag_constants.SERVING],
signature_def_map={
'sp500_prediction':
prediction_signature
})
builder.save()
According to the code listed above, we will use TensorFlow Model Builder to export the model into an appropriate format. Specifically, what we have to do is to instantiate the model builder object, passing the path to a model being exported as a single argument of its constructor. Then, we have to create two tensor context objects for either model’s input or outputs, passed as a single argument of saved_model.utils.build_tensor_info(…) method. We will use the values of model.input and model.outputs[0] variables as the parameters passed to the following method. Specifically, model.input and model.output variables are input and output tensor objects of the model built. Since, our model has only one output, we will use the first element of the model.output array as the parameter passed to the build_tensor_info(…) method.
After that, we must create the model’s signature object as the result of build_signature_def(…) method invocation. The following method has three main arguments such as a model’s inputs and output context objects, as well as the prediction method when overridden. Each specific input and output within the model signature has its own unique alias, such as ‘TICKERS’ or ‘SP500INDEX’. Since we’re about to use the default prediction method for this model, we must specify its name by using the pre-defined constant PREDICT_METHOD_NAME.
Since the model signature object has been instantiated, we need to invoke the add_meta_graph_and_variables(…) method, having three main arguments, including the session object, the default serving alias as well as the model’s signature object, previously created. Specifically, this method creates a meta-graph, that represents the model’s structure context, stores the model’s variables and tensors into the model along with the meta-graph created.
After creating the model in-memory, we must finally call the builder.save() method to save the model. The model being saved has the following directory structure:
8889/
variables/
variables.data-?????-of-?????
variables.index
saved_model.pb
In this case, the name of the model’s root directory is the version of the model being exported. The ‘variables’ directory contains two files such as variables.data and variables.index containing the input and output model’s tensors as well as the other variables and its values saved to the model. The saved_model.pb file contains the meta-graph of the model saved.
How to Run this Script
Since we've already written a Python script that builds and exports the model, let's discuss how to run this script on the development machine. First of all, the Python language and development tools must be installed. In this case, I strongly recommend that the Anaconda environment is downloaded from this link, and installed locally on the development machine.
After that, we must open the Anaconda3 command prompt and change to the directory in which sp500_retrain.tar.gz archive was extracted. This directory contains several files such as sp500_retrain.py, utility.py and sp500.csv. We must locate the sp500_retrain.py script and run it using the following command:
python sp500_retrain.py
Alternatively, we can use Anaconda's Jupytter Notebook to execute the following script. In this case, what we have to do is to open sp500_retrain.py and utility.py scripts in a text editor and paste them to the newly created Python script in the Jupytter Notebook, and then click on the Run button to execute the script:

Finally, the sp500_model directory is created. Also, the following script generates a mentioned above JPG-image, (e.g., sp500_results.jpg) visualizing the prediction results. After the model has been created by the script being executed, we can deploy this model for serving.
Serve the Model using TensorFlow Model Server (TMS)
After the model has been successfully built and exported, now we can serve the model using TensorFlow Model Server. In the previous article, we’ve already discussed how to install and configure TensorFlow Model Server on the SAP-HANA virtual server. To be able to serve this model, all that we have to do first is to login as tmsadm user to our running instance of SAP-HANA server bash console using PuTTY SSH-client. Then, we have to upload our model (e.g., ‘sp500_model’ directory) to the /home/tmsadm/exports/ location on the server, via FTP-connection. The /home/tmsadm/exports/ directory already contains models.config file previously created during the server configuration phase. We must modify this configuration file as follows:
model_config_list: {
config: {
name: "sp500_model",
base_path: "/tf_models/sp500_model",
model_platform: "tensorflow"
},
}
Since we've uploaded the model directory and made changes to the configuration file, we can start our Docker container with TensorFlow Model Server by using the following command in the tmsadm user bash-console:
sudo docker run -it -d -p 8500:8500 -p 9000:9000
--mount type=bind,source=/home/tmsadm/export/models.config,
target=/tf_models/config/models.config --mount type=bind,
source=/home/tmsadm/export/sp500_model/,target=/tf_models/sp500_model/
--entrypoint "/bin/sh" tensorflow/serving:latest -c "tensorflow_model_server
--port=8500 --rest_api_port=9000 --model_config_file=/tf_models/config/models.config"
To check if the current model is successfully served, we must make the following RESTFul API request using CURL utility:
curl -X GET http://192.168.0.131:9000/v1/models/sp500_model
As the response for this request, we will get the following data in JSON-format:
{
"model_version_status": [
{
"version": "8889",
"state": "AVAILABLE",
"status": {
"error_code": "OK",
"error_message": ""
}
}
]
}
The following status messages indicates that the model is properly served and we can use it in the SAP-HANA SQL-engine to perform the specific predictions in the SAP-HANA server backend.
Conclusion
In this article, we've thoroughly discussed on how to build, export and server S&P 500 Index prediction model. We've learned how to use various of techniques that allow us to design an architecture of an effective RNN-based model and use it to make the specific S&P 500 Index indicator values predictions. Along with the model architecture, we've found out how to implement this model by using Python's TensorFlow Keras library, and export it for serving using TensorFlow Model Server.
History
- 13th September, 2019: Initial version published
