1. Introduction
Multidimensional arrays are widely used in programming languages, for instance, to represent matrices, tensors. In C and C++, standard arrays have fixed sizes. In this article, I will look at how flexible, resizable arrays can be implemented.
The approach is rather simple. A sample array definition can look as follows:
flat_array<double, 3> d10{ {{1,2,3,3.5},{4,5,6,6.5},{7,8,9,10},{11,12,13,14}},
{ {111,211,311,31.5},{41,51,61,61.5},{711,866,966,1066},{1166,1266,1366,1466}} };
We would like to be able to access elements, either using square brackets:
d10[1][2][3]
or round brackets:
d10(1, 2, 3)
In addition, we would like to be able to swap subarrays, using a specially defined swap function:
swap(d10(1,2), d10(0,3));
A general option for creation of a multidimension array with default initialization is:
flat_array<element_type,m> array_name(n1,n2,...,nm);
The array can be resized as follows:
array_name.resize(k1,k2,...,km);
The implementation is written in C++17 [1]. The benchmarks are provided, comparing the implementation with standard C-style arrays and Boost multi_array [2].
2. What Is Available Now
Here is an example of a C/C++ two-dimensional array definition:
double x[2][3] = {{3.3, 4.1, 5.0}, {23.1, 63,7, 81.2}};
But this array is of fixed dimensions. We cannot redefine its sizes.
Another approach is to use pointers. Here is a definition of an array 5x3:
double **y;
y = new double*[5];
for (std::size_t i = 0; i < 5; i++)
{
y[i] = new double[3];
for (std::size_t j = 0; j < 3; j++)
{
y[i][j] = i * 3 + j + 0.2;
}
}
for (std::size_t i = 0; i < 5; i++)
{
for (std::size_t j = 0; j < 3; j++)
{
std::cout << y[i][j] << " ";
}
std::cout << std::endl;
}
The above code will output the following values:
0.2 1.2 2.2
3.2 4.2 5.2
6.2 7.2 8.2
9.2 10.2 11.2
12.2 13.2 14.2
Although the second approach is more flexible – it allows to use variables or expressions instead of fixed values, 5 and 3, it requires more effort to clear the memory when we want to discard this array.
In C++, there are also vectors. Here is a similar example using vectors:
std::vector<std::vector<double>> y;
y.resize(5);
for (std::size_t i = 0; i < 5; i++)
{
y[i].resize(3);
for (std::size_t j = 0; j < 3; j++)
{
y[i][j] = i * 3 + j + 0.2;
}
}
Although no effort is needed to dispose this array, there is still some effort to create it. The more dimensions there are, the more loops we have to write.
3. Two Basic Approaches to Multidimensional Array Implementation
3.1. Multilevel Approach
This approach is similar to the one discussed above using pointers: several fragments of memory are allocated as shown in Figure 1.
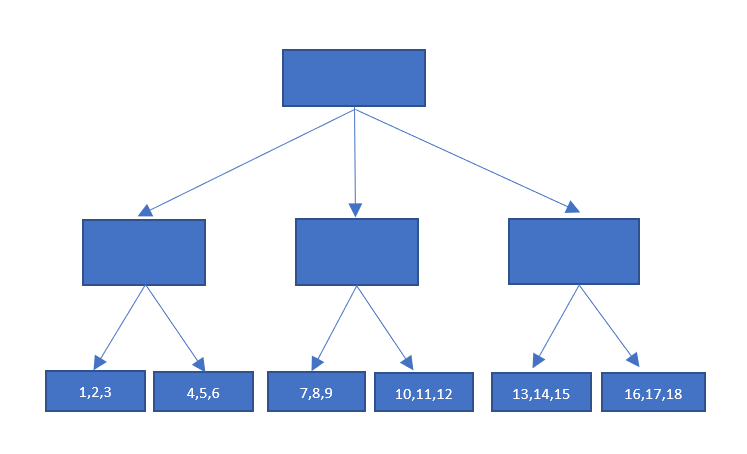
Figure 1. Multilevel Approach to Multidimensional Array Representation
The issue here is that the memory used by the arrays is fragmented.
3.2. Flat Approach
In this case, an array is represented by a block of memory, where all the values are stored one after another without any gaps. In practice, the C-style standard array is exactly represented like that:
int a[3][2][3]={{{1,2,3},{4,5,6}},{{7,8,9},{10,11,12}},{{13,14,15},{16,17,18}}};
Internally, it is stored as a sequence of values (usually 4 bytes each):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
In order to access the element a[i][j][k], we have to calculate the index, as follows:
index = i*2*3+j*3+k
Say, we want to access the element a[2][1][1]:
index = 2*6+1*3+1 = 16
Since we count the position indices from 0, this index corresponds to the value 17.
3.3. Which Approach Is Better?
The multilevel approach uses fragmented memory, which means that accessing elements randomly will require loading different fragments into the processor cache and may slow down the execution. On the other hand, swapping subarrays (say, rows in a matrix) can be faster since it requires swapping pointers. In the flat approach, the only way to swap two subarrays is to swap them element by element, which can be rather slow.
The multilevel approach may have an advantage if the whole array does not fit into one memory slot -- issues arise with limited addressing in the implementation. Often, in a 32-bit implementation, a single allocated memory slot should not be greater than 232 or even 231 bytes, depending on the implementation. This issue does not arise in a 64-bit implementation.
The advantage of the flat approach is that the whole array can be mapped into an image, where pixels occupy a fixed block of memory outside the array structure. In this case, an image can easily be treated as a two-dimensional array of pixels.
Taking all those points into consideration, I will look into the flat approach:
- The access to single elements will be faster.
- The array can be mapped onto a memory block, which can easily be used to represent, for instance, images as two-dimensional arrays.
4. Implementation
4.1. Getting Indices and Sizes Right
4.1.1. Defining Dimensions
Let's start from the very beginning: the template parameters, the types, the class member variables:
template <class Elem, int Dim, bool AllocationFlag = true>
class flat_array
{
public:
using size_type = std::size_t;
using dimension_index = int;
private:
size_type *m_dimensions; size_type m_dataSize; Elem *m_data;
The choice of types: std::size_t is in general recommended for representing sizes. I have chosen int for the type of the dimension index: I found that GNU C++ is particularly sensitive to template deduction when it comes to unsigned integer type. I wouldn't like to write 1U, 2U, 3U for dimensions. Let's look at the flat_array template parameters:
Elem is the type of the array element.Dim is the number of dimensions.AllocationFlag is the flag informing whether the dimensions and the elements are allocated or referenced.
The number of dimensions is fixed for each flat_array object, but since we sometimes need occasionally to point to the m_dimensions field from another structure, we define it as a pointer, not as a C array, which would be tempting to do.
We have to define member functions to set the sizes and to get the index of an element. We will use variadic templates to do that. The advantage of the C++17 is that we can use constexpr if, which makes the code shorter.
The SetSizes function is used to set the sizes for all the dimensions. It is a recursive templated function. When calling this function on top level, the pos parameter should be 0: for instance, SetSizes(0,3,2,3) can be called for a three-dimensional array to define dimnsions 3x2x3.
template<class... T>
void SetSizes(dimension_index pos, size_type m1, T...k1)
{
if (pos == 0)
{
m_dataSize = 1;
}
m_dimensions[pos] = m1;
m_dataSize *= m1;
if constexpr (sizeof...(k1) > 0)
{
SetSizes(pos + 1, k1...);
}
}
One of the constructors for flat_array can be as follows:
template<class... T>
flat_array(size_type m1, T... k1)
{
m_dimensions = new size_type[Dim]; SetSizes(0, m1, k1...);
m_data = new Elem[m_dataSize]; for (size_type i = 0; i < m_dataSize; i++)
{
m_data[i] = Elem(); }
}
The memory is not allocated for m_data in SetSizes because we reserve the ability to refer to external memory blocks, like image pixels for instance. In this case, a special flag variable is defined inside the class:
bool m_owner = true;
Here is an example of a 6-dimensional array definition:
flat_array p(3,4,10,9,10,2);
The constructor to use an external block of memory will be as follows:
template<class ...T>
flat_array(const Dimensions<T...>& s, Elem* data)
{
m_dimensions = new size_type[Dim];
std::copy(s.m_dimensions, s.m_dimensions + Dim, m_dimensions);
m_dataSize = s.m_dataSize;
m_owner = false;
m_data = data;
}
Dimensions is an additional class that is used to define flat array dimensions.
Here is a code sample that uses this constructor:
std::vector<std::string> d{ "A","B","C","APPLE","BANANA","CHERRIES",
"One","Two","Three","?","!","*" };
flat_array<std::string, 2> p{ Dimensions{ 4,3 },d.data() };
4.1.2. Defining an Element Position From Its Indices
In order to be able to access an element, we should know its index in the flat memory block, which should be calculated from its indices in the multidimensional array.
Say the dimensions of the multidimensional array are: n0,n1,n2,...,nm. If the indices of an element are j0,j1,...,jm-1jm, then the index i in the flat memory block will be calculated as follows:
i =( j0×n1× ... ×nm)+(j1×n2× ... ×nm)+...+(jm-1×nm)+ jm
Here is the code that implements the function GetIndex:
template<class... T>
size_type GetIndex(dimension_index pos, size_type prevIndex, size_type m1, T...k1) const
{
size_type index = (prevIndex* m_dimensions[pos]) + m1;
if constexpr (sizeof...(k1) > 0)
{
return GetIndex(pos + 1, index, k1...);
}
else
{
return index;
}
}
The first two parameters -- pos and prevIndex -- are used for the recursive call, and when called on top level should be set to 0. For instance, if we'd like to write an operator() to access a single array element, we do it as follows:
template<class ...T>
Elem& operator()(size_type k0, T...indices)
{
return m_data[GetIndex(0, 0, k0, indices...)];
}
But we are going to do better than that. We have to consider subarrays -- the case when we only supply a few indices at the beginning, similar to accessing a row in a matrix. We look at it below.
4.1.3. Resizing
The resizing of the flat array can be defined as follows:
template<class...T>
void resize(size_type m1, T...k1)
{
if constexpr (AllocationFlag)
{
if (m_owner)
{
SetSizes(0, m1, k1...);
delete[] m_data;
m_data = new Elem[m_dataSize];
for (size_type i = 0; i < m_dataSize; i++)
{
m_data[i] = Elem();
}
}
else
{
throw FlatArrayException("cannot resize a non-owner");
}
}
else
{
throw FlatArrayException("cannot resize a non-owner");
}
}
Resizing is only allowed for the owners.
4.2. Accessing Subarrays and Elements
4.2.1 What Syntax to Use for Indexing
Now we are ready to access subarrays and elements. The question is how are we going to index arrays. There are two options in C++:
x[i][j][k]
x(i, j, k)
The first one is traditional, coming from C and is still used to access standard fixed size arrays. The second one is shorter. I think most programmers prefer the third option, which cannot be used at present:
x[i, j, k]
Here the comma operator, coming from C, has a different meaning: effectively if there are no side effects in evaluating i and j, the last expression will be equivalent to calculating:
x[k]
That is not what we tried to achieve. There is a proposal in the C++ Working Group not to allow a comma operator in indices: you will still be able to write it but as follows:
x[(i, j, k)]
If this proposal is adopted, then after a few years a multiparameter operator[] will be introduced in C++, and the developers wil be able to use a better syntax. But before that happens, we are stuck with the two choices that I mentioned above.I will provide both implementations – using the single-parameter operator[] and the multiparameter operator().
4.2.2. Getting a Reference to a subarray and Indexing
If we use an element-access syntax, but provide fewer indices than the number of dimensions, we will get a subarray. In terms of programming, we create an flat_array object that should reference the internals of the original flat array but with fewer dimensions. Here is the code for constructing a subarray using only one index p:
template<bool AllocationFlag2>
flat_array(const flat_array<Elem, Dim + 1, AllocationFlag2>& s, size_type p)
{
m_dataSize = s.m_dataSize / s.m_dimensions[0];
m_dimensions = s.m_dimensions + 1;
size_type m = 1;
for (dimension_index i = 0; i < Dim; i++)
{
m *= m_dimensions[i];
}
m_data = s.m_data + p * m;
}
This code will only be used if Dim >= 1. The original array, used as a parameter, will have at least 2 dimensions. That means the created object will not be an element, but a subarray.
Let's now write the operator[] definition (the allocation flag is set to false):
decltype(auto) operator[](size_type p)
{
if constexpr (Dim != 1)
{
return flat_array<Elem, Dim - 1, false>(*this, p); }
else
{
return m_data[p]; }
}
The return value decltype(auto) ensures that the right type is deducted, which will be either the value type of a subrarray or a reference type to an element. We have to write a similar definition for the const option. Using this syntax, we can access any element of a flat_array object. The decltype construct is very well explained by Scott Meyers [3]. The main idea is that decltype(auto) ensures that expressions are returned as value types, and l-values are returned by reference. Using auto&& instead of decltype(auto) would be a mistake, because the subarray will be returned as r-value reference, not as a copy, and outside the operator[] body it won't exist. Using simple auto will return everything by value and we won't get a reference to m_data[p].
A few words about constexpr if. It makes it much easier to write functions that depend on static conditions. Without it, in C++, we would use SFINAE ("Substitution Failure Is Not An Error"), the concept where a template may produce a syntactically illegal construct during substitution and be eliminated from the code as a result. Some of the typically used constructs would be std::enable_if or std::enable_if_t, which can test a static expression and as a result, produce a required of illegal type, for instance, that could be a function return. But this technique is more complicated and would require to write a function for each static condition.
Let's us look at the operator() definition:
template<class ...T>
decltype(auto) operator()(size_type k0, T...indices)
{
if constexpr (sizeof...(T) == Dim - 1)
{
return m_data[GetIndex(0, 0, k0, indices...)]; }
else if constexpr (Dim >= 2 && sizeof...(T) == 0)
{
return flat_array<Elem, Dim - 1, false>(*this, k0); }
else if constexpr (Dim >= 2 && sizeof...(T) < Dim - 1)
{
return flat_array<Elem, Dim - 1, false>(*this, k0)(indices...); }
}
The const option of this member function should be written as well.
4.3. Swapping subarrays or Elements
Say, you would like to swap rows of a matrix, which means you have to access two subarrays of a two-dimensional array and swap them. We have discussed how to access subarrays. Now we have to consider how to swap their elements.
In order to swap elements, there are several options. We have to consider all the options for a global two-parameter swap function. Here are the headers enlisted in the class as friends:
template<class Element, int Dim1, bool allocation>
friend void swap(flat_array<Element, Dim1, allocation>& x,
flat_array<Element, Dim1, allocation>& y);
template<class Element, int Dim1, bool allocation>
friend void swap(flat_array<Element, Dim1, allocation>& x,
flat_array<Element, Dim1, !allocation>& y);
template<class Element, int Dim1, bool allocation1, bool allocation2>
friend void swap(flat_array<Element, Dim1, allocation1>&& x,
flat_array<Element, Dim1, allocation2>&& y);
template<class Element, int Dim1, bool allocation1, bool allocation2>
friend void swap(flat_array<Element, Dim1, allocation1>&& x,
flat_array<Element, Dim1, allocation2>& y);
template<class Element, int Dim1, bool allocation1, bool allocation2>
friend void swap(flat_array<Element, Dim1, allocation1>& x,
flat_array<Element, Dim1, allocation2>&& y);
Let's look at the implementation of the first function outside the class:
template<class Element, int Dim1, bool allocation>
void swap(flat_array<Element, Dim1, allocation>& x, flat_array<Element, Dim1, allocation>& y)
{
if (x.m_dataSize != y.m_dataSize)
{
std::ostringstream ss;
ss << "swap. arrays of different sizes.
size1: " << x.m_dataSize << " size2: " << y.m_dataSize;
throw FlatArrayException(ss.str());
}
bool simple = allocation && x.m_owner && y.m_owner;
if (simple)
{
std::swap(x.m_data, y.m_data); }
else
{
for (std::size_t i = 0; i < x.m_dataSize; i++)
{
std::swap(x.m_data[i], y.m_data[i]); }
}
}
If both are true owners (the allocation flag is true and the m_owner field is true), then the data pointers can be swapped; otherwise, we can swap the subarrays element by element.
The second swap is dealing with cases when at least one of the allocation flags is false, which means that one of the parameters is not a true owner. In this case, the only option is to swap the elements:
template<class Element, int Dim1, bool allocation>
void swap(flat_array<Element, Dim1, allocation>& x, flat_array<Element, Dim1, !allocation>& y)
{
if (x.m_dataSize != y.m_dataSize)
{
std::ostringstream ss;
ss << "swap. arrays of different sizes.
size1: " << x.m_dataSize << " size2: " << y.m_dataSize;
throw FlatArrayException(ss.str());
}
for (std::size_t i = 0; i < x.m_dataSize; i++)
{
std::swap(x.m_data[i], y.m_data[i]);
}
}
The other three functions can be implemented using these two swap implementations:
template<class Element, int Dim1, bool allocation1, bool allocation2>
void swap(flat_array<Element, Dim1, allocation1>&& x,
flat_array<Element, Dim1, allocation2>&& y)
{
swap(x, y);
}
template<class Element, int Dim1, bool allocation1, bool allocation2>
void swap(flat_array<Element, Dim1, allocation1>&& x,
flat_array<Element, Dim1, allocation2>& y)
{
swap(x, y);
}
template<class Element, int Dim1, bool allocation1, bool allocation2>
void swap(flat_array<Element, Dim1, allocation1>& x,
flat_array<Element, Dim1, allocation2>&& y)
{
swap(x, y);
}
Here is an example of using swap:
flat_array<double, 3> d10{ {{1,2,3,3.5},{4,5,6,6.5},{7,8,9,10},
{11,12,13,14}},{ {111,211,311,31.5},{41,51,61,61.5},
{711,866,966,1066},{1166,1266,1366,1466}} };
flat_array<double, 3> d20{ {{301,302,333,3453.5},{41,51,61,61.5},
{71,81,91,100},{511,512,513,514}},{ {5111,5211,5311,531.5},
{641,651,661,661.5},{8711,8866,8966,1866},{2166,2266,2366,2466}} };
flat_array<double, 1> dxx{ -30.5,-40,-60,-75.1 };
swap(dxx, d10[1][2]);
swap(d10(0,2), d10(1,3));
std::cout << "d10" << std::endl;
std::cout << d10; swap(d10, d20);
std::cout << "d10" << std::endl;
std::cout << d10; std::cout << "d20" << std::endl;
std::cout << d20;
The above fragment of code will output the following values:
d10
1 2 3 3.5
4 5 6 6.5
1166 1266 1366 1466
11 12 13 14
--------------------------------------------------------------------------------
111 211 311 31.5
41 51 61 61.5
-30.5 -40 -60 -75.1
7 8 9 10
--------------------------------------------------------------------------------
d10
301 302 333 3453.5
41 51 61 61.5
71 81 91 100
511 512 513 514
--------------------------------------------------------------------------------
5111 5211 5311 531.5
641 651 661 661.5
8711 8866 8966 1866
2166 2266 2366 2466
--------------------------------------------------------------------------------
d20
1 2 3 3.5
4 5 6 6.5
1166 1266 1366 1466
11 12 13 14
--------------------------------------------------------------------------------
111 211 311 31.5
41 51 61 61.5
-30.5 -40 -60 -75.1
7 8 9 10
--------------------------------------------------------------------------------
4.4. Assignment and Pitfalls
As was explained above, access to a subarray creates a reference class. The issue is that if this subarray is assigned to an auto variable, this variable will not be its own array, but a reference to an existing one, which means that changing its contents will change the contents of the original array.
Let's look at the following code:
flat_array<double, 2> d20_1 = d20[1];
d20_1(0, 1) = 888.777; auto d20_2 = d20[1]; d20_2(0, 2) = 555.333;
If you don't want to create a reference object, then use the full declaration of the flat_array during initialization, as in case of d20_1 above.
4.5. Iterators
The defined iterators make it possible to process all the elements of a flat array as if it was a single one-dimensional array. For example, let's look at the following fragment of code with a for-loop (it uses an iterator inside):
flat_array<double, 3> d10{ {{1,2,3,3.5},{4,5,6,6.5},{7,8,9,10},{11,12,13,14}},
{{111,211,311,31.5},{41,51,61,61.5},{711,866,966,1066},{1166,1266,1366,1466}} };
for (auto x : d10)
{
std::cout << x << " ";
}
std::cout << std::endl;
This code will output the following values:
1 2 3 3.5 4 5 6 6.5 7 8 9 10 11 12 13 14 111 211 311 31.5 41 51
61 61.5 711 866 966 1066 1166 1266 1366 1466
5. Benchmarks
The code was tested both in VS 2017 (using C++17 in the language selection) and in GCC C++ 7.1. The flat_array implementation was compared with C single-block array representation, C-style multiplelevel arrays representation and Boost multi_array.
For Boost multi_array, I had to implement an extra function for swapping subarrays.
The C single-block representation means that an array with dimensions MxNxP is allocated as follows:
double* x = new double[M*N*P];
Access to an element [i][j][k] is as follows:
x[i*N*P+j*P+k]
In a multilevel approach, the array is allocated as follows:
double*** y = new double**[M];
for (std::size_t i = 0; i < M; i++)
{
y[i] = new double*[N];
for (std::size_t j = 0; j < N; j++)
{
y[i][j] = new double[P];
}
}
The access is simple:
y[i][j][k]
The benchmarks ran on the system with Intel Core I7-4970 3.6GHz, 16GB Memory. The produced results are shown in Figure 2. The benchmarks tests are as follows:
- Random Access 800x800x800; 10 million random 3-dimensional array elements are summed up.
- Random Access 25x25x25x25x25x25; 10 million 6-dimensional array elements are summed up.
- 10x5000x5000, Swapping k and k; the array is transposed so that the last two indices are swapped.
- 800x800x800 i,j,k→k,i,j; the array is transposed so that an element at position [i,j,k] was moved to position [k,i,j].
- 25x25x25x25x25x25 i,j,k,l,m,n→n,i,j,k,l,m; the array is transposed so that an element at position [i,j,k,l,m,n] was moved to position [n,i,j,k,l,m].

Figure 2. Benchmarks of various multidimensional arrays representations.
It is quite clear that flat_array performs better at random-access, whereas multilevel approach is better when big array fragments are transposed. Boost muti_array objects perform slower that flat_array particularly in transposition. The signal-block arrays are at the basis of flat_array implementation, not surprisingly, they perform in general a bit faster than flat_array objects.
In VS 2017, the code was compiled in Release mode, 64-bit with the following optimization options:

In GNU C++ it was compiled as follows:
g++ -O3 -std=c++17 -I"/boost_1_71" -m64 FlatArrayBenchmarks.cpp -o FlatArrayBenchmarks.exe
References
- Working Draft, Standard for Programming Language C++. http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2017/n4713.pdf
- Boost C++ Libraries. https://www.boost.org/
- Scott Meyers. "Effective Modern C++", 2015. https://moodle.ufsc.br/pluginfile.php/2377667/mod_resource/content/0/Effective_Modern_C__.pdf
History
- 13th November, 2019: Initial version
